Complete Solutions to NCERT SECTION (Exercise 7.2) of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| MTG IIT JEE FOUNDATION | NCERT SECTION (Exercise 7.2) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
Triangle ABC is an isosceles triangle with `AB=AC`. Bisectors of `angleB and angleC` intersect each other at O. join `A-O` and prove that
`OB=OC`
View SolutionIn `DeltaA B C`, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that `DeltaA B C`is an isosceles triangle in which `A B\ =\ A C`.
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
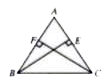
`DeltaABE~=DeltaACF`
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
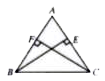
AB=AC, i.e., ABC is an isosceles triangle.
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that`/_A B D\ =/_A C D`
View SolutionDABC is an isosceles triangle in which `A B"\ "="\ "A C` . Side BA is produced to D such that `A D"\ "="\ "A B` (see Fig. 7.34). Show that `/_B C D` is a right angle.
View SolutionABC is a right angled triangle in which `angleB=90^(@) and AB=BC`. Find `angleA and angleC`.
View SolutionShow that the angles of an equilateral triangle are `60o`each.
View Solution
NCERT SECTION (Exercise 7.2) questions and complete solutions for chapter TRIANGLES of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS TRIANGLES
- EXERCISE (Multiple Choice Questions) (ASSERTION & REASON TYPE)
- EXERCISE (Multiple Choice Questions) (COMPREHENSION TYPE)
- EXERCISE (Multiple Choice Questions) (LEVEL-1 )
- EXERCISE (Multiple Choice Questions) (LEVEL-2 )
- EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
- EXERCISE (Multiple Choice Questions) (PASSAGE)
- EXERCISE (Subjective Problems) ( Integer/Numerical Value Type)
- EXERCISE (Subjective Problems) ( Long Answer Type)
- EXERCISE (Subjective Problems) ( Short Answer Type)
- EXERCISE (Subjective Problems) (Very Short Answer Type)
- ILLUSTRATIONS
- NCERT SECTION (Exercise 7.1)
- NCERT SECTION (Exercise 7.2)
- NCERT SECTION (Exercise 7.3)
- NCERT SECTION (Exercise 7.4)
- NCERT SECTION (Exercise 7.5)
- OLYMPAID/ HOTS CORNER
- SOLVED EXAMPLES