Complete Solutions to EXERCISE (Comprehension Type PASSAGE- III ) of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| MTG IIT JEE FOUNDATION | EXERCISE (Comprehension Type PASSAGE- III ) |
| Number Of Questions | 3 |
| Academic Year | 2023-24 |
The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of `DeltaABC` is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=

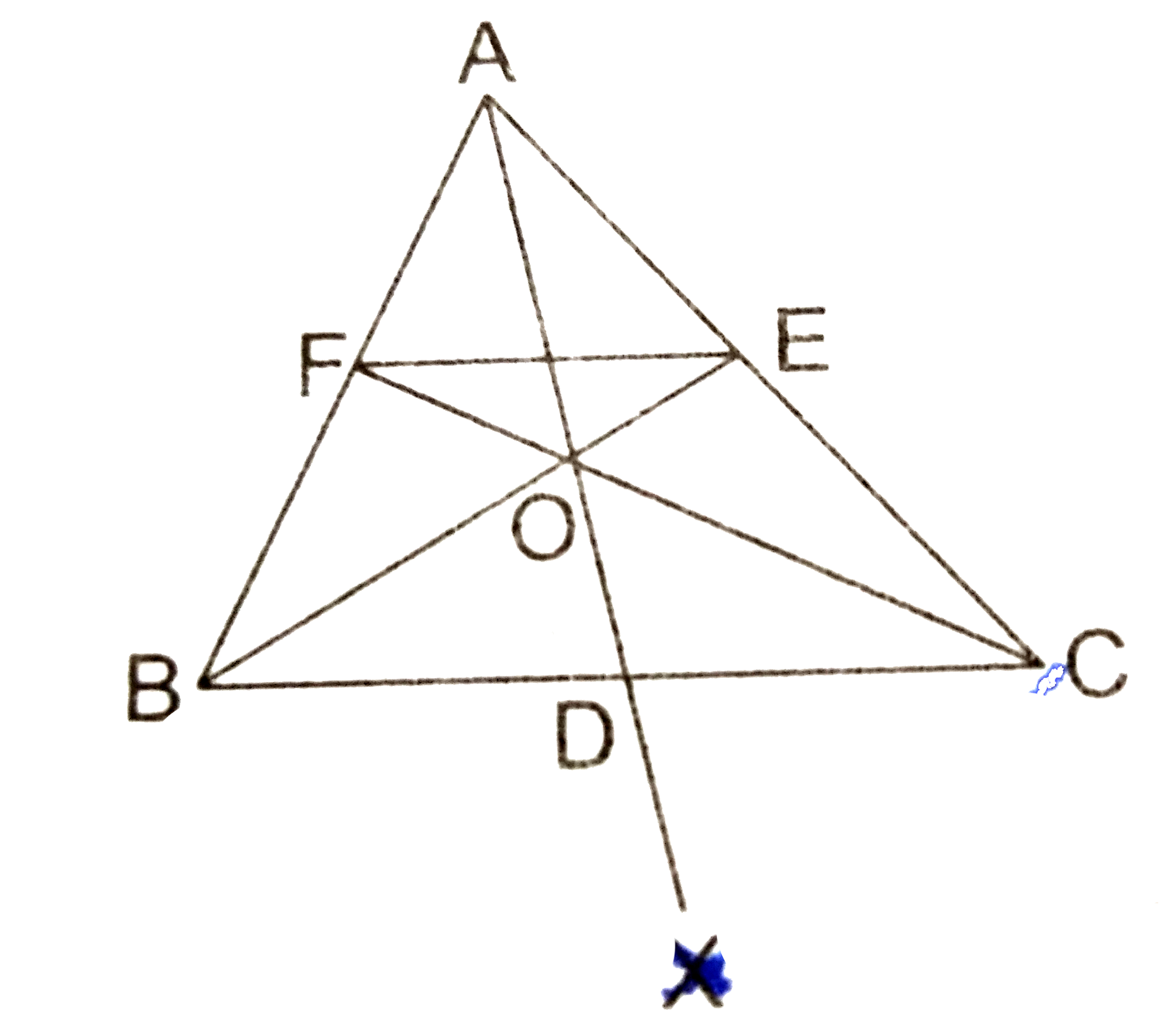
View SolutionIn the given figure, sid BC of `Delta ABC` is biseted at D and O is any point AD.BO and CO produced meet AC and AB at E and F respetively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that `AO:AX=AF:AB` and show that `EF||BC`.
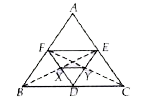
View SolutionIn the given figure, D, E and F are the midpoints of the sides BC, CA and AB of `DeltaABC. BE` bisect DF at X while CF bisect DE at Y, then BC = a XY. Find a.
View Solution
EXERCISE (Comprehension Type PASSAGE- III ) questions and complete solutions for chapter QUADRILATERALS of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS QUADRILATERALS
- EXERCISE (Assertion & Reason Type)
- EXERCISE (Comprehension Type PASSAGE- III )
- EXERCISE (Comprehension Type PASSAGE-I)
- EXERCISE (Comprehension Type PASSAGE-II )
- EXERCISE (Integer/Numerical Value Type)
- EXERCISE (Match the Following)
- EXERCISE (Multiple Choice Questions) (LEVEL-1 )
- EXERCISE (Multiple Choice Questions) (LEVEL-2 )
- EXERCISE (Subjective Problems) (Long Answer Type)
- EXERCISE (Subjective Problems) (Short Answer Type)
- EXERCISE (Subjective Problems) (Very Short Answer Type)
- ILLUSTRATIONS
- NCERT SECTION (Exercise 8.1 )
- NCERT SECTION (Exercise 8.2 )
- Olympiad/HOTS CORNER
- SOLVED EXAMPLES