Complete Solutions to ILLUSTRATIONS of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| MTG IIT JEE FOUNDATION | ILLUSTRATIONS |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
In a parallelogram `A B C D ,` prove that sum of any two consecutive angles is `180^0dot`
View Solution`A B C D` is a parallelogram. `L\ a n d\ M` are points on `A B\ a n d\ D C` respectively and `A L=C M` . Prove that `L M\ a n d\ B D` bisect each other.
View SolutionIf `A B C D` is a quadrilateral in which `A B C D` and `A D=B C ,` prove that `/_A` =`/_B` .
View Solution`A B C D` is a parallelogram. `A B` is produced to `E` so that `B E=A B` . Prove that `E D` bisects `B Cdot`
View SolutionIn Figure, `D ,E` and `F` are, respectively the mid-points of sides `B C ,C A` and `A B` of an equilateral triangle `A B C` . Prove that `D E F` is also an equilateral triangle.
View SolutionLet ABC be a triangle, right-angled at B and D be the midpoint of AC. Show that DA = DB = DC.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
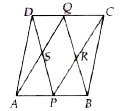
(i) APCQ is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

PSQR is a parallelogram.
View Solution
ILLUSTRATIONS questions and complete solutions for chapter QUADRILATERALS of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS QUADRILATERALS
- EXERCISE (Assertion & Reason Type)
- EXERCISE (Comprehension Type PASSAGE- III )
- EXERCISE (Comprehension Type PASSAGE-I)
- EXERCISE (Comprehension Type PASSAGE-II )
- EXERCISE (Integer/Numerical Value Type)
- EXERCISE (Match the Following)
- EXERCISE (Multiple Choice Questions) (LEVEL-1 )
- EXERCISE (Multiple Choice Questions) (LEVEL-2 )
- EXERCISE (Subjective Problems) (Long Answer Type)
- EXERCISE (Subjective Problems) (Short Answer Type)
- EXERCISE (Subjective Problems) (Very Short Answer Type)
- ILLUSTRATIONS
- NCERT SECTION (Exercise 8.1 )
- NCERT SECTION (Exercise 8.2 )
- Olympiad/HOTS CORNER
- SOLVED EXAMPLES