Complete Solutions to EXERCISE (Subjective Problems) (Very Short Answer Type) of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| MTG IIT JEE FOUNDATION | EXERCISE (Subjective Problems) (Very Short Answer Type) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Find the measure of all the angles of a parallelogram, if one angle of the adjacent angles is `20^(@)` less than thrice the smallest angle
View SolutionIn Fig. 13.98, `BE _|_ AC. AD` is any line from A to `BC` intersecting `BE` in `H.P. O and R` are respectively the mid-points of `AH, AB and BC.` Prove that `anglePOR = 90^@.`
View SolutionIn a parallelogram `A B C D ,\ /_D=135^0,` determine the measures of `/_A\ a n d\ /_B`
View SolutionABCD is a parallelogram in which `angleA = 78^(@)`. Compute `angleB, angleC and angleD`.
View SolutionIn Figure, `A B C D` is a parallelogram in which `/_A=60^0` . If the bisectors of `/_A` and `/_B` meet at `P ,` prove that `A D=D P ,P C=B C` and `D C=2A Ddot` Figure
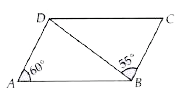
View SolutionIn the given figure, ABCD is a parallelogram in which `angleDAB = 60^(@) and angleDBC = 55^(@)` . Compute `angleCDB and angleADB` .
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionIn the adjoining figure, `DeltaABC` is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of `Delta` ABC. Prove that `anglePAC=angleBCAand squareABCP` is a parallelogram.
View SolutionABCD is a rectangle with `angleABD=50^(@)` . Determine `angleDBC` .
View SolutionIn `DeltaABC, angleA=50^(@), angleB=30^(@) and angleC=100^(@)` What are the angles of the triangle formed by joining the midpoints of the sides of this triangle?
View Solution
EXERCISE (Subjective Problems) (Very Short Answer Type) questions and complete solutions for chapter QUADRILATERALS of MTG IIT JEE FOUNDATION of Class 9
All Exercises from MTG IIT JEE FOUNDATION Class 9 MATHS QUADRILATERALS
- EXERCISE (Assertion & Reason Type)
- EXERCISE (Comprehension Type PASSAGE- III )
- EXERCISE (Comprehension Type PASSAGE-I)
- EXERCISE (Comprehension Type PASSAGE-II )
- EXERCISE (Integer/Numerical Value Type)
- EXERCISE (Match the Following)
- EXERCISE (Multiple Choice Questions) (LEVEL-1 )
- EXERCISE (Multiple Choice Questions) (LEVEL-2 )
- EXERCISE (Subjective Problems) (Long Answer Type)
- EXERCISE (Subjective Problems) (Short Answer Type)
- EXERCISE (Subjective Problems) (Very Short Answer Type)
- ILLUSTRATIONS
- NCERT SECTION (Exercise 8.1 )
- NCERT SECTION (Exercise 8.2 )
- Olympiad/HOTS CORNER
- SOLVED EXAMPLES