Complete Solutions to Problems From NCERT/exemplar of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| NAGEEN PRAKASHAN | Problems From NCERT/exemplar |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionDiagonal AC of a paraleligram ABCD bisects `angleA` (sec figure). Show that:
(i) it bisects `angleC` also (ii) ABCD is a rhombus.
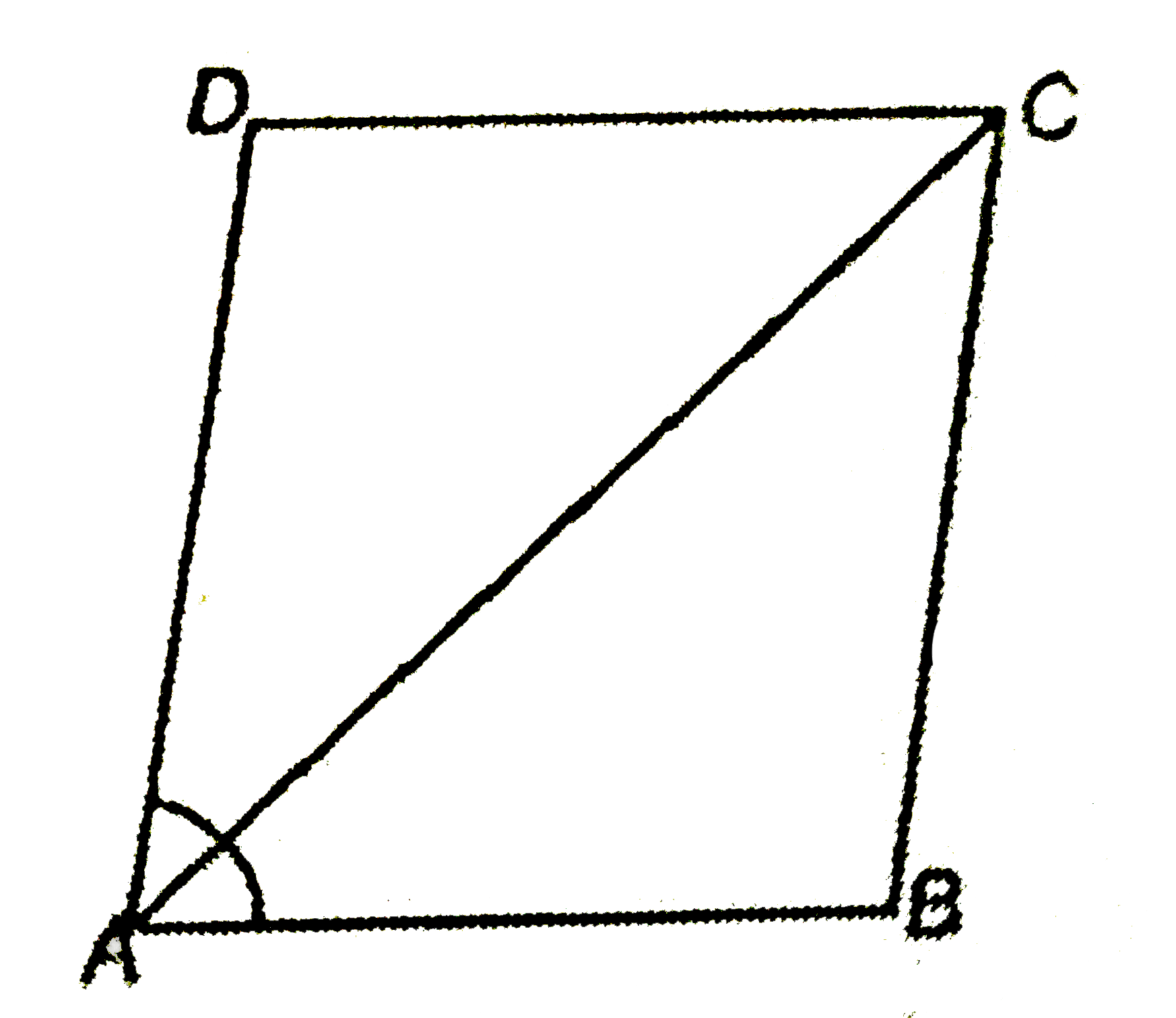
View SolutionABCD is a rectangle in which diagonal AC bisects `angleA` as well as `angleC.` Show that
(i) ABCD is a square
(ii) diagonal BD bisects `angleB`
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
`{:((i)DeltaAPD~=CQB,(ii)AP=CQ),((iii)DeltaAQB~=DeltaCPD,(iv)AQ=CP),((v)APCQ "is a parallelogram.",):}` ltbegt
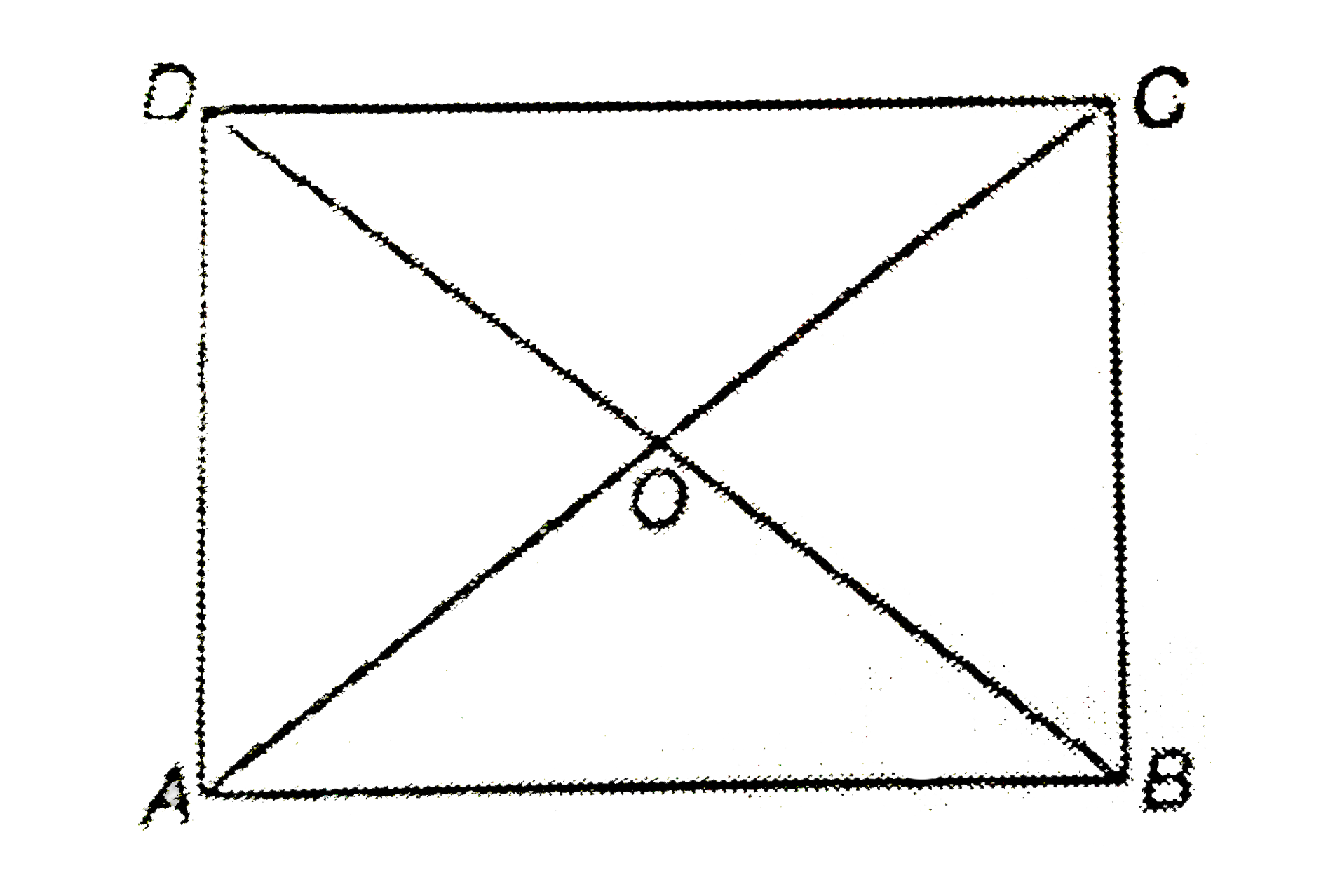
View SolutionP, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC `bot` BD. Prove that PQRS is a rectangle.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
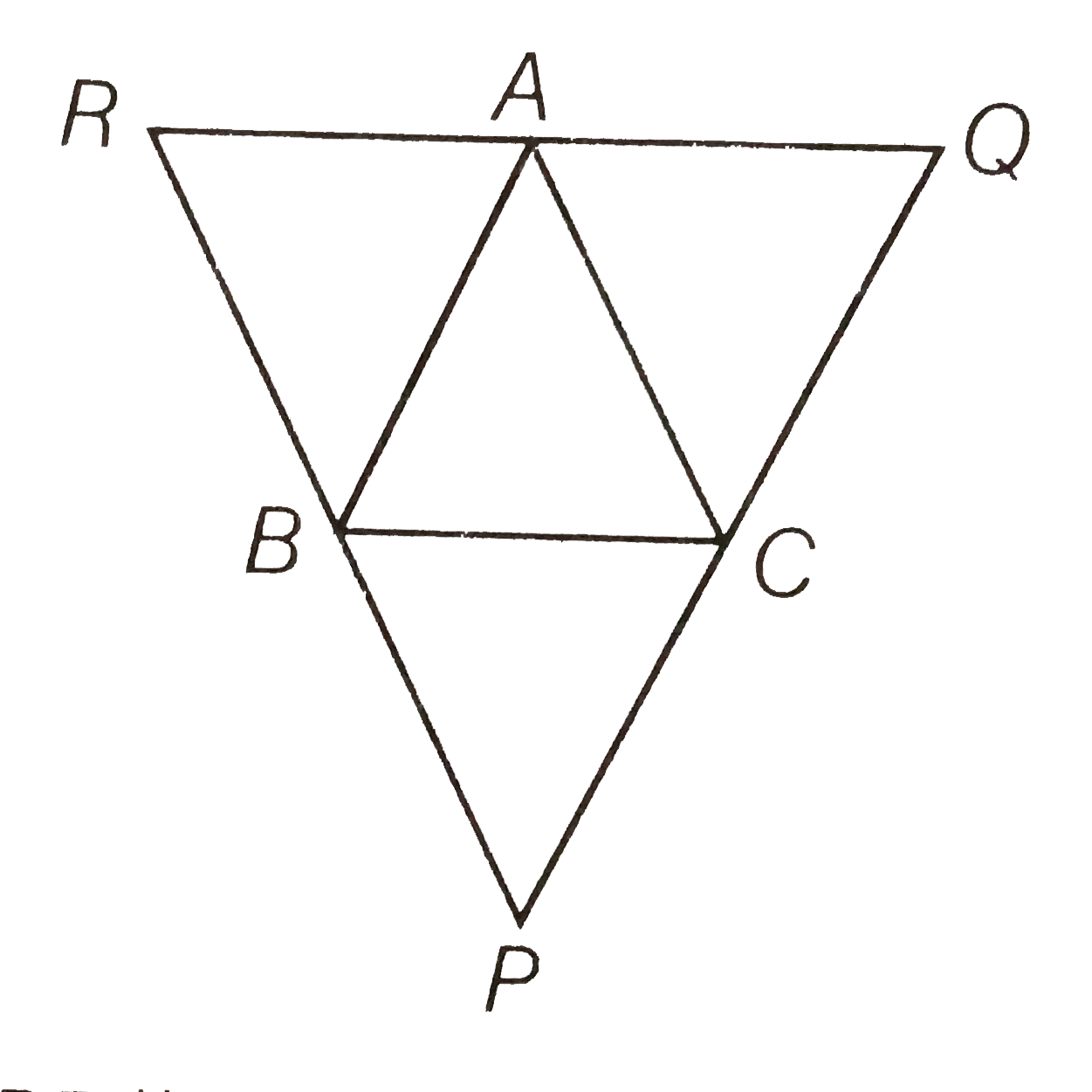
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a `Delta`ABC as shown in figure. Show that `BC=(1)/(2)QR`.
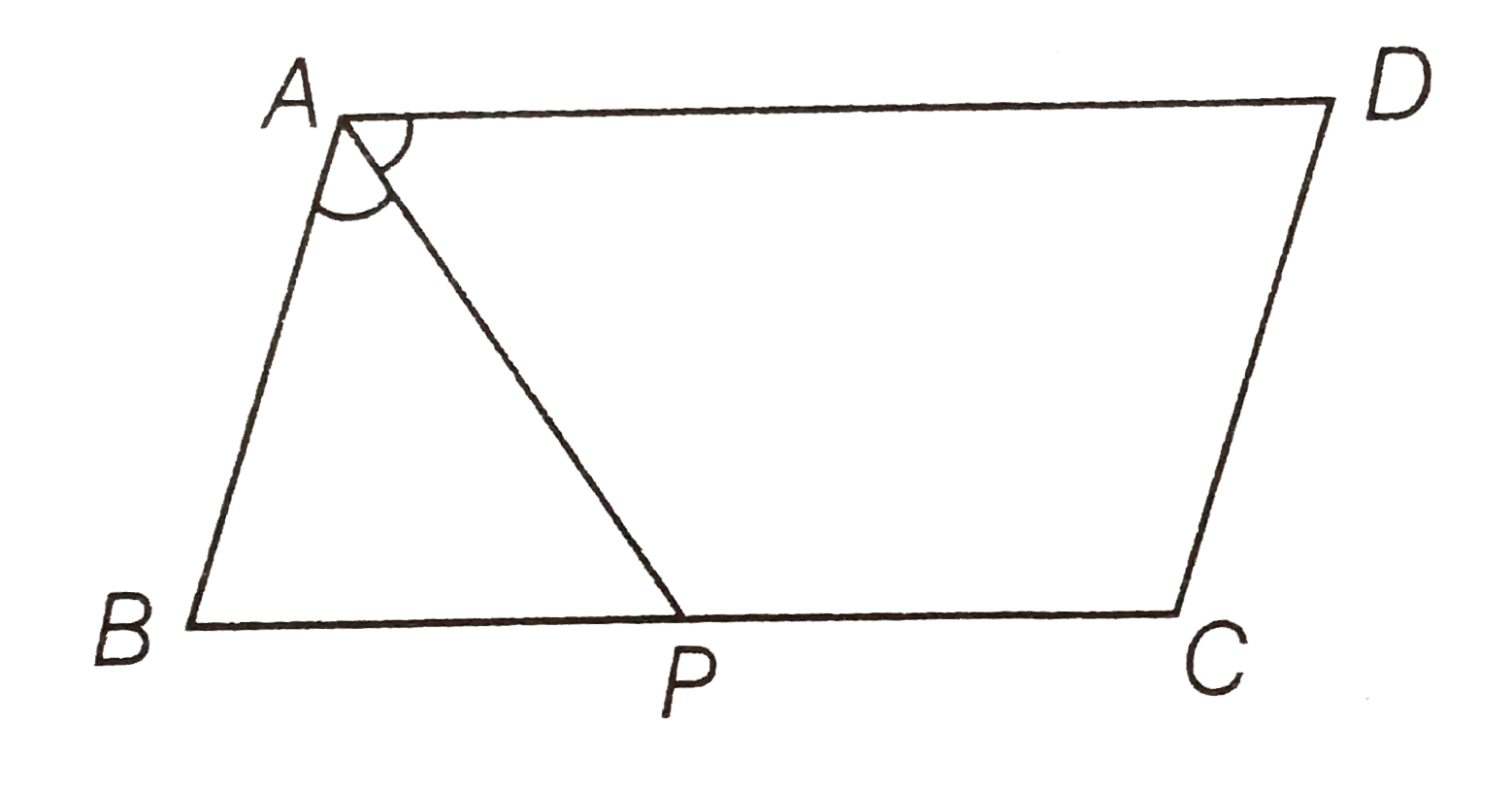
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that `angleBAP=angleDAP`. Prove that AD = 2CD.
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.

View SolutionIn figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
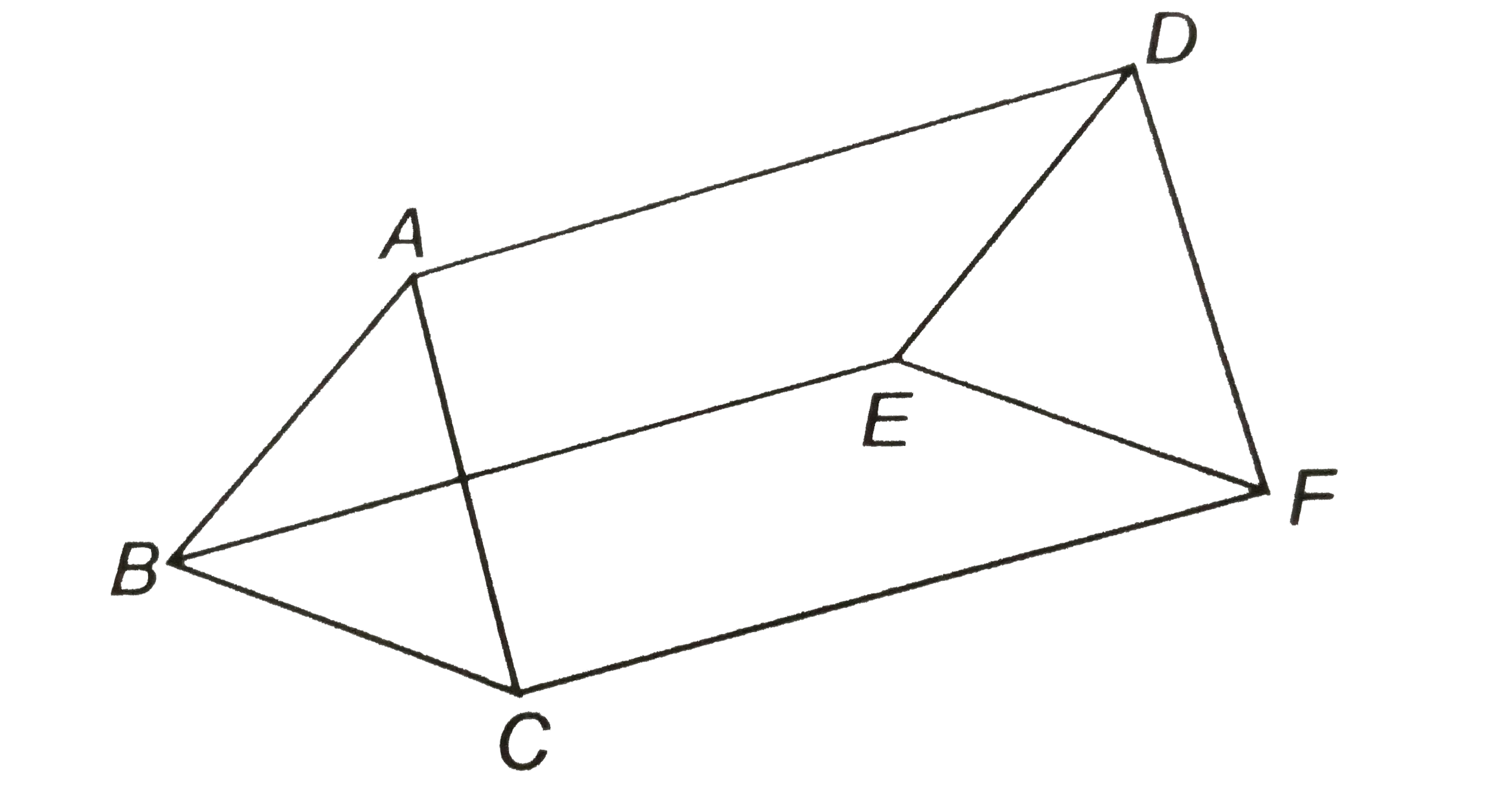
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View Solution
Problems From NCERT/exemplar questions and complete solutions for chapter QUADRILATERALS of NAGEEN PRAKASHAN ENGLISH of Class 9