Complete Solutions to Revision Exercise (short Answer Questions ) of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| NAGEEN PRAKASHAN | Revision Exercise (short Answer Questions ) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
In an isosceles-trapezium, show that the opposite angles are supplementary.
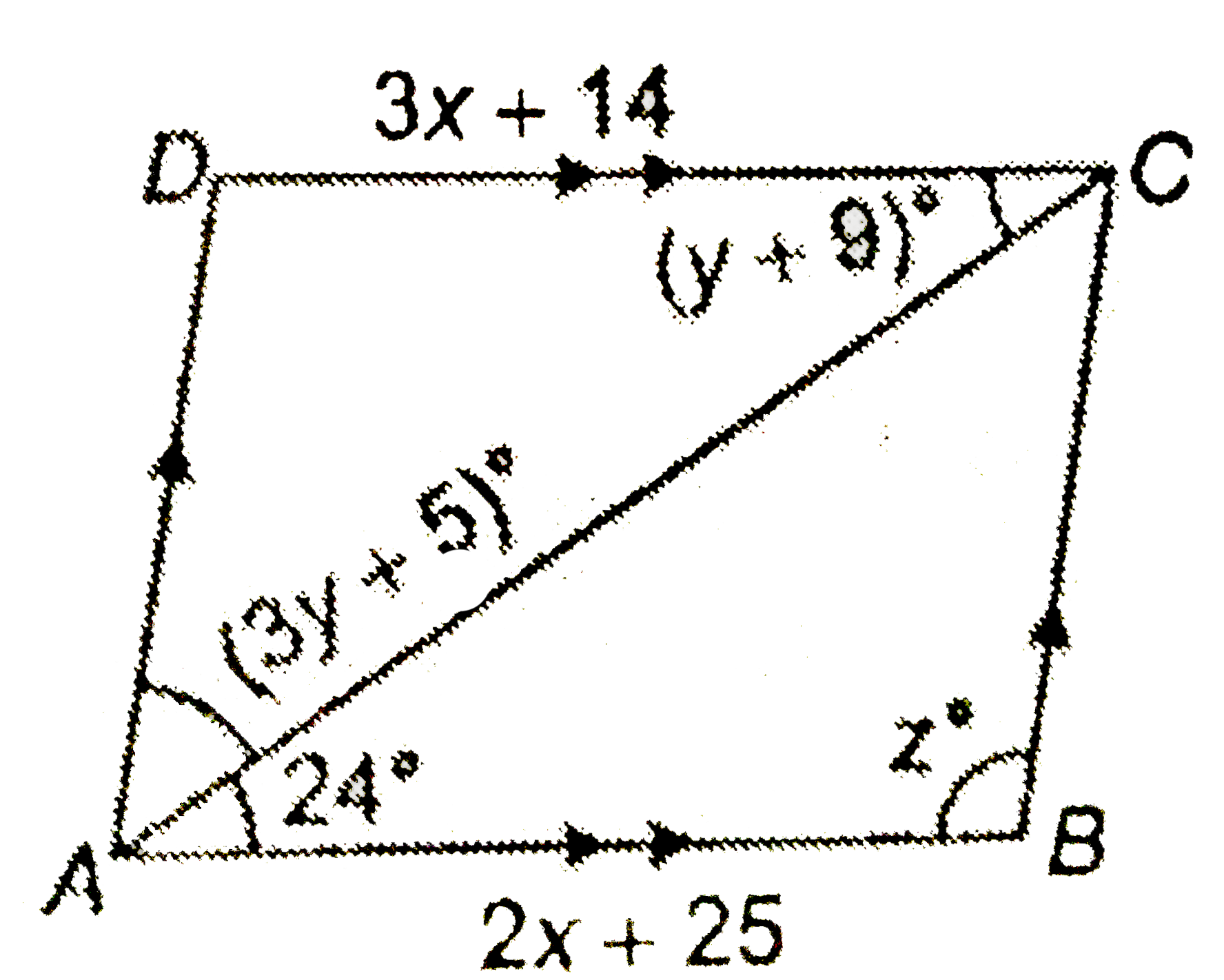
View SolutionIn the given figure ABCD is a parallelogram. AB = (2x+25) cm, CD = (3x+14) cm, `angleB=z^(o), angleBAC=24^(@),angleDAC=3y+5^(@)and angleDCA=y+9^(@),` find the values of x, y and z.
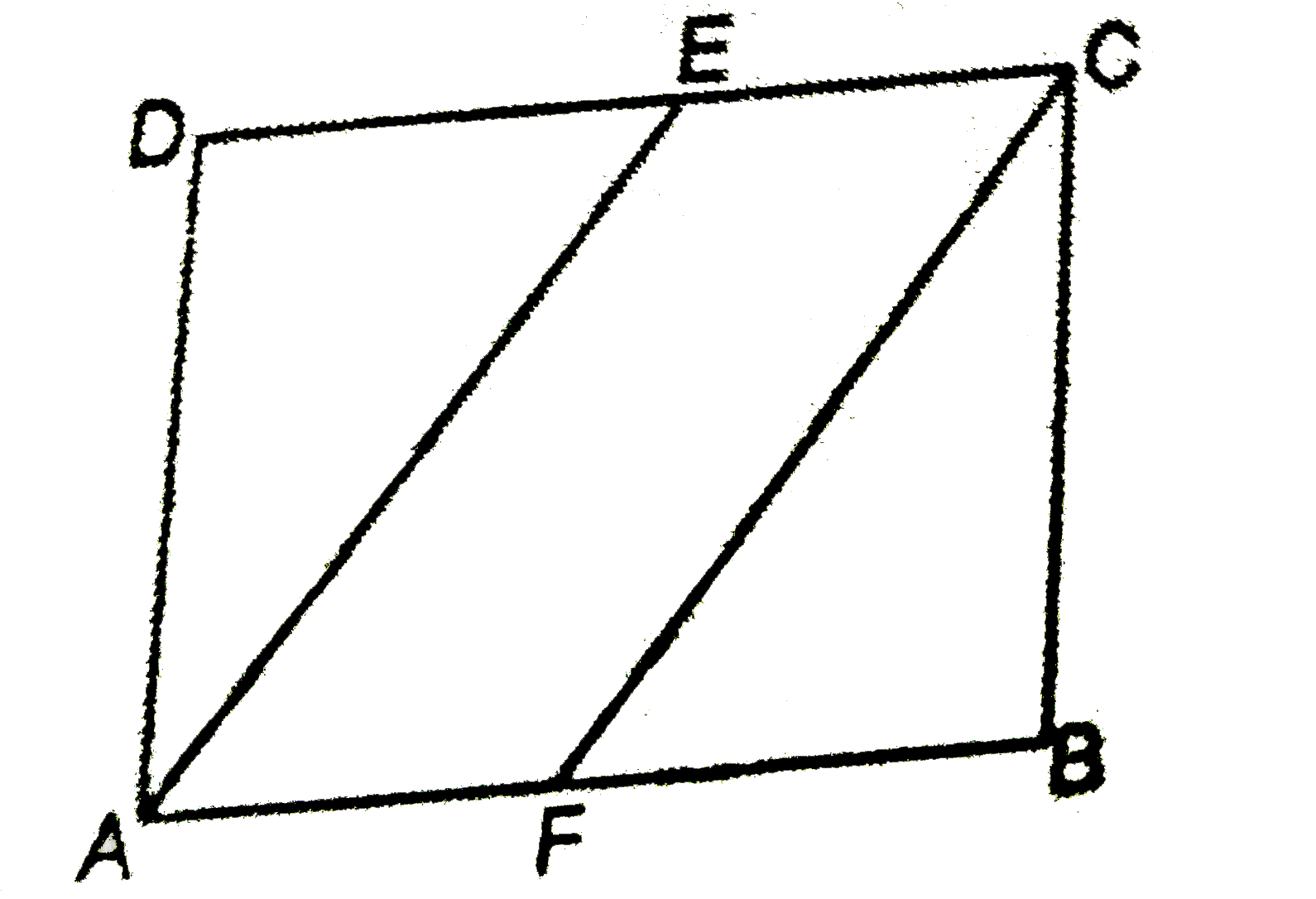
View SolutionABCD is a parallelogram and AE and CF bisect `angleA and angleC` respectively. Prove that `AE"||"FC.`
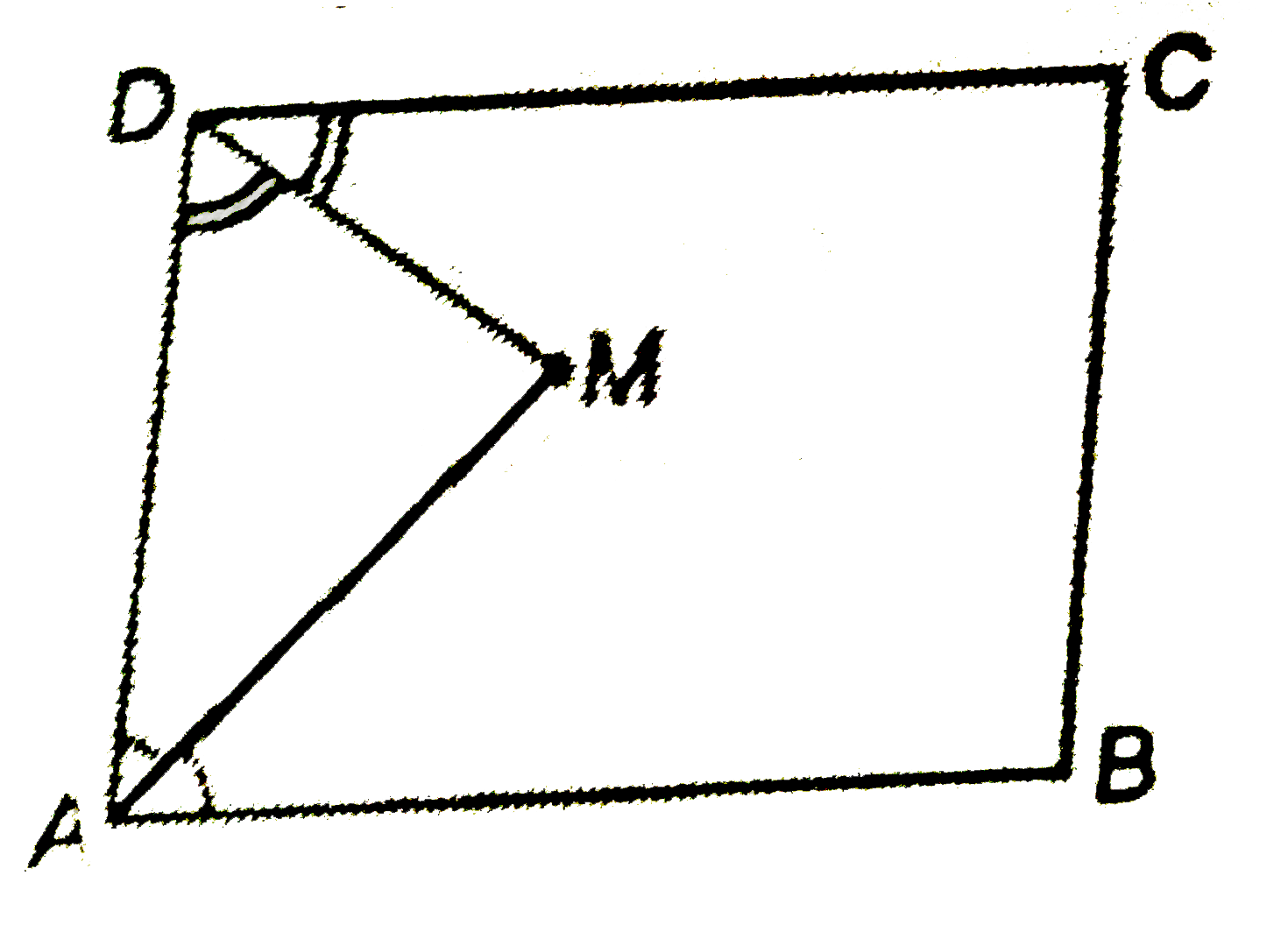
View SolutionIn the given figure, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that `angleAMD = 90^(@).`
View SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.

View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC is perpendicular bisector of BD
View SolutionIn the adjoining figure, ABCD is a rhombus and ABE is an equilateral triangle. If `angleBCD=70^(@),` find
`(a)angleADE" "(b)angleBDE" "(c)angleBED`

View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that `EF=1/2(AB-CD).`

View SolutionIn a quadrilateral ABCD the linesegment bisecting `angleC and angleD` meet at E. Prove that `angleA+angleB=2angleCED.`
View Solution
Revision Exercise (short Answer Questions ) questions and complete solutions for chapter QUADRILATERALS of NAGEEN PRAKASHAN ENGLISH of Class 9