Complete Solutions to Quadrilaterals of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| NCERT EXEMPLAR | Quadrilaterals |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Three angles of a quadrilateral are `75^(@),90^(@) and 75^(@)`, then the fourth angle is
View SolutionA diogonal of a rectangle is inclined to one side of the rectangle at `25^(@)`. The acute angle between the diagonals is
View SolutionABCD is a rhombus such that `angleACB=40^(@)`, then `angleADB` is
View SolutionThe quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
View SolutionThe quadrilateral formed by joining the mid-points of the side for quadilateral PQRS, taken in order, is a rhombus, if
View SolutionIf angles A, B, C and D of the quadrilateral ABCD, taken in order are in the ratio 3 : 7 : 6 : 4, then ABCD is a
View SolutionIf bisectors of `angleA and angleB ` of a quadrilateral ABCD intersect each other at P, of `angleB and angleC` at Q, of `angleC and angleD` at R and of `angleD and angleA` at S, then PQRS is a
View SolutionIf `APB` and `CQD` are two parallel lines, then the bisectors of the angles `APQ, BPQ, CQP` and `PQD` form
View SolutionThe figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is
View SolutionD and E are the mid-points of the sides AB and AC of `Delta`ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only, if
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If `angleDAC=32^(@) and angleAOB=70^(@)`, then `angleDBC` is equal to
View SolutionWhich of the following is not true for a parallelogram ?
View SolutionD and E are the mid-points of the side AB and AC, respectively, of `Delta`ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
View SolutionDiagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.
View SolutionCan the angles `110^(@), 80^(@), 70^(@) and 95^(@)` be the angles of a quadrilateral ? Why or why not?
View SolutionIn quadrilateral ABCD, `angleA+angleD= 180^(@)`. What special name can be given to this quadrilateral?
View SolutionAll the angles of a quadrilateral are equal. What special name is given to this quadrilateral ?
View SolutionDiagonals of a rectangle are equal and perpendicular. Is this statement true ? Give reason for your answer.
View SolutionCan all the four angles of a quadrilateral be obtuse angles ? Give reason for your answer.
View SolutionIn `Delta`ABC, AB = 5cm , BC = 8 cm and CA = 7cm. If D and E are respectively the midd-points of AB and BC, determine the length of DE.
View SolutionIn the figure, it is given that BDEF and FDCE are parallelogram. Can you say that BD = CD ? Why or why not?
View SolutionIn figure, ABCD and AEFG are two parallelograms. If `angleC = 55^(@)`, then determine `angleF`.
View SolutionCan all the angles of a quadrilateral be acute angles ? Give reason for your answer.
View SolutionCan all the angles of a quadrilateral be right angles ? Give reason for your answer.
View SolutionDiagonals of a quadrilateral ABCD bisect each other. If `angleA=35^(@), ` determine `angleB`.
View SolutionOpposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
View SolutionOne angle of a quadrilateral is `108^0` and the remaining three angles are equal. Find the three equal angles.
View SolutionABCD is a trapezium in which `AB||DC and angleA=angleB=45^(@)`. Find angles C and D of the trapezium.
View SolutionThe angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is `60^(@)`. Find the angles of the parallelogram.
View SolutionABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionE is the mid-point of the side AD of the trapezium ABCD with `AB||DC`. A line through E drawn parallel to AB intersects BC at F. then
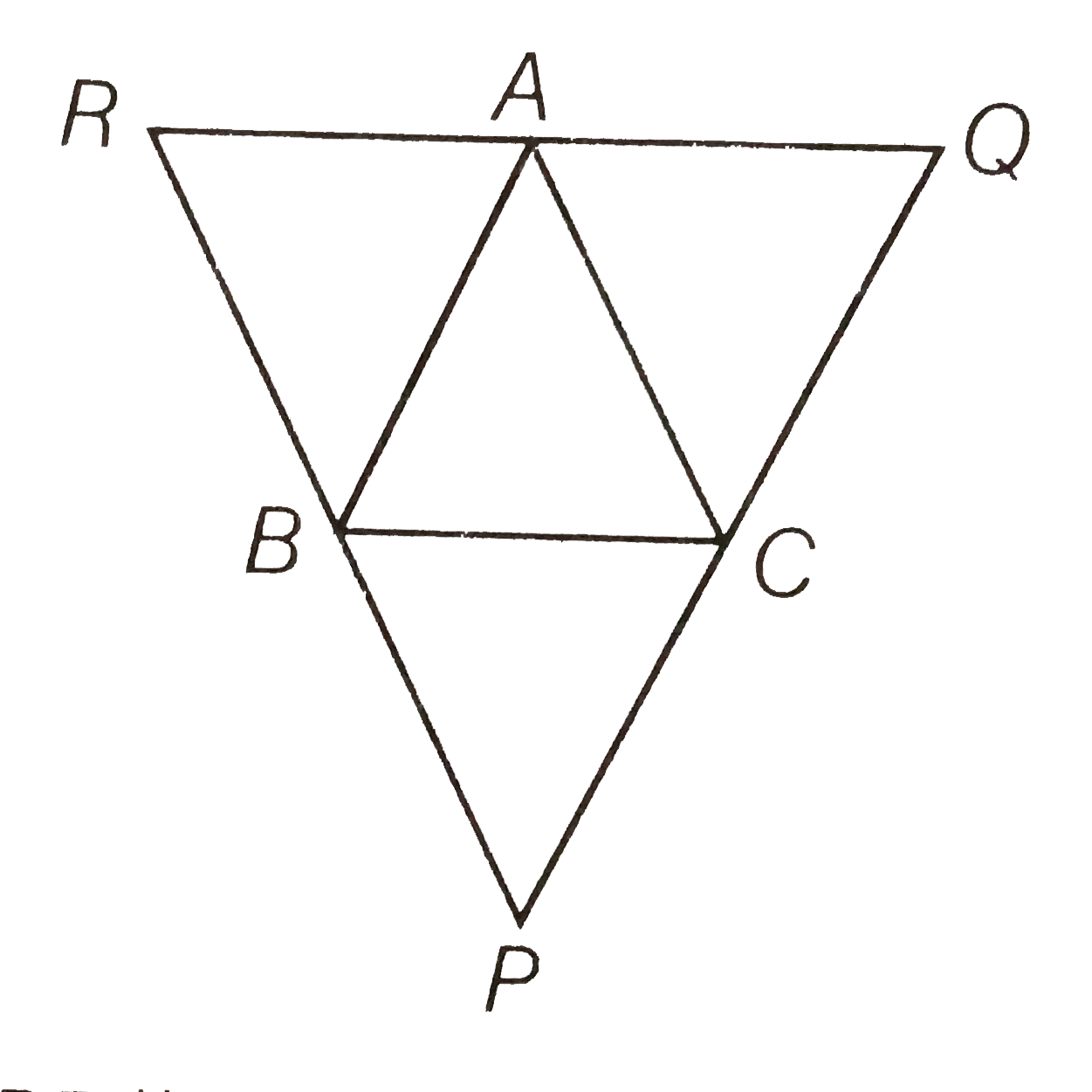
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a `Delta`ABC as shown in figure. Show that `BC=(1)/(2)QR`.
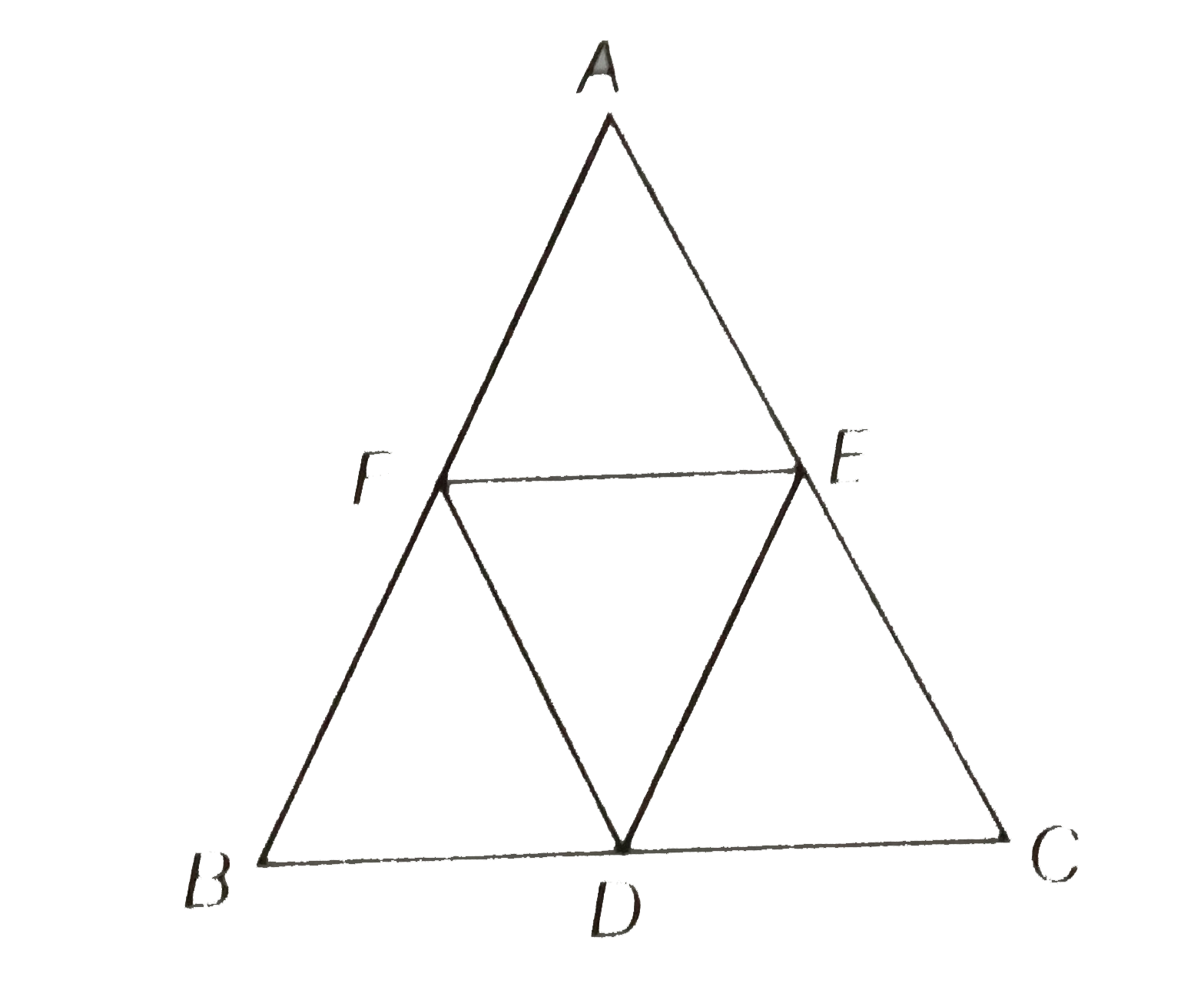
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral `Delta`ABC. Show that `Delta`DEF is also an equilateral triangle.
View SolutionPoints P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
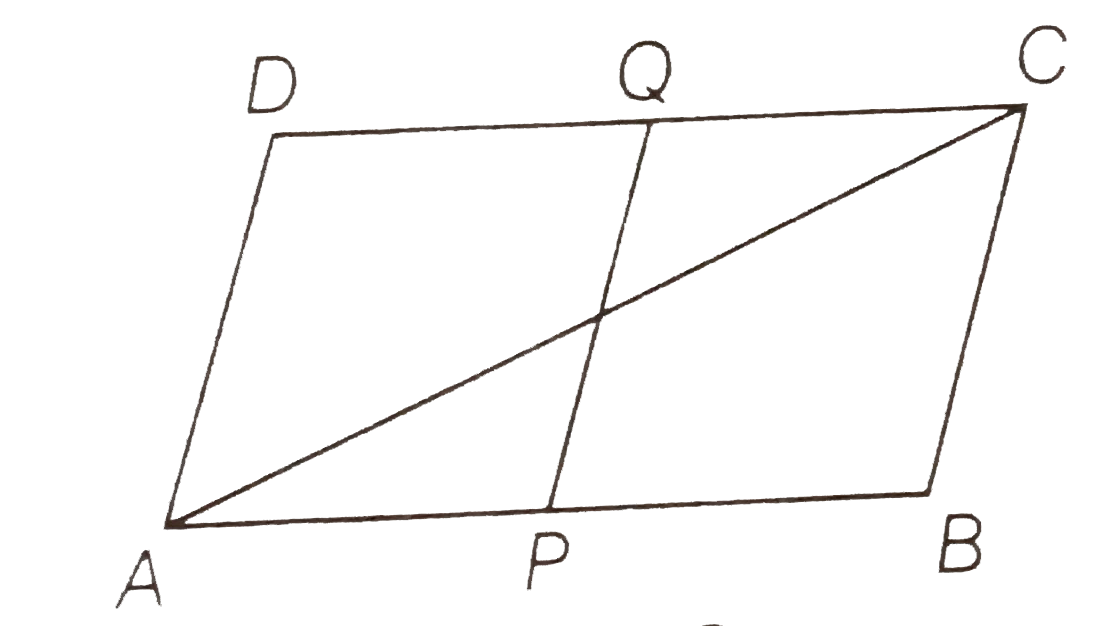
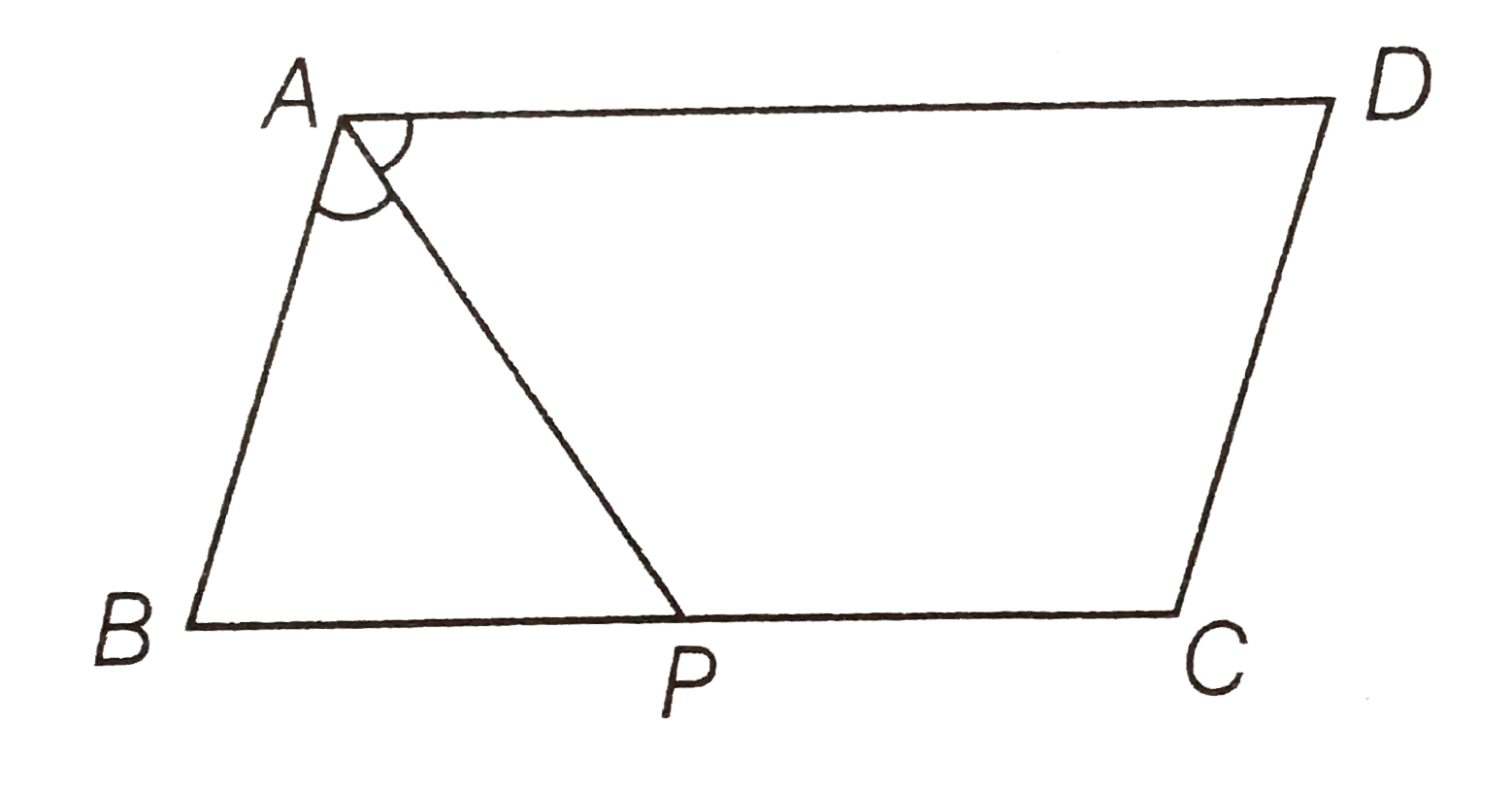
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that `angleBAP=angleDAP`. Prove that AD = 2CD. ltBrgt
View SolutionA square is incribed in an isoceles right triangle, so that the square and the triangle have one angle common. Show that the vertex of the sqare opposite the vertex of the common angle bisects the hypotenuse.
View SolutionIn a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of `angleA` meets DC in E. AE and BC produced meet at F. Find the length of CF.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. then the quadrilateral PQRS is a
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and `ACbotBD`. Prove that PQRS is a square.
View SolutionIf diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle. Also, prove that it is a rhombus.
View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram. (ii) DPBQ is a parallelogram. (iii) PSQR is a parall
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that `angleA=angleB and angleC= angleD`.
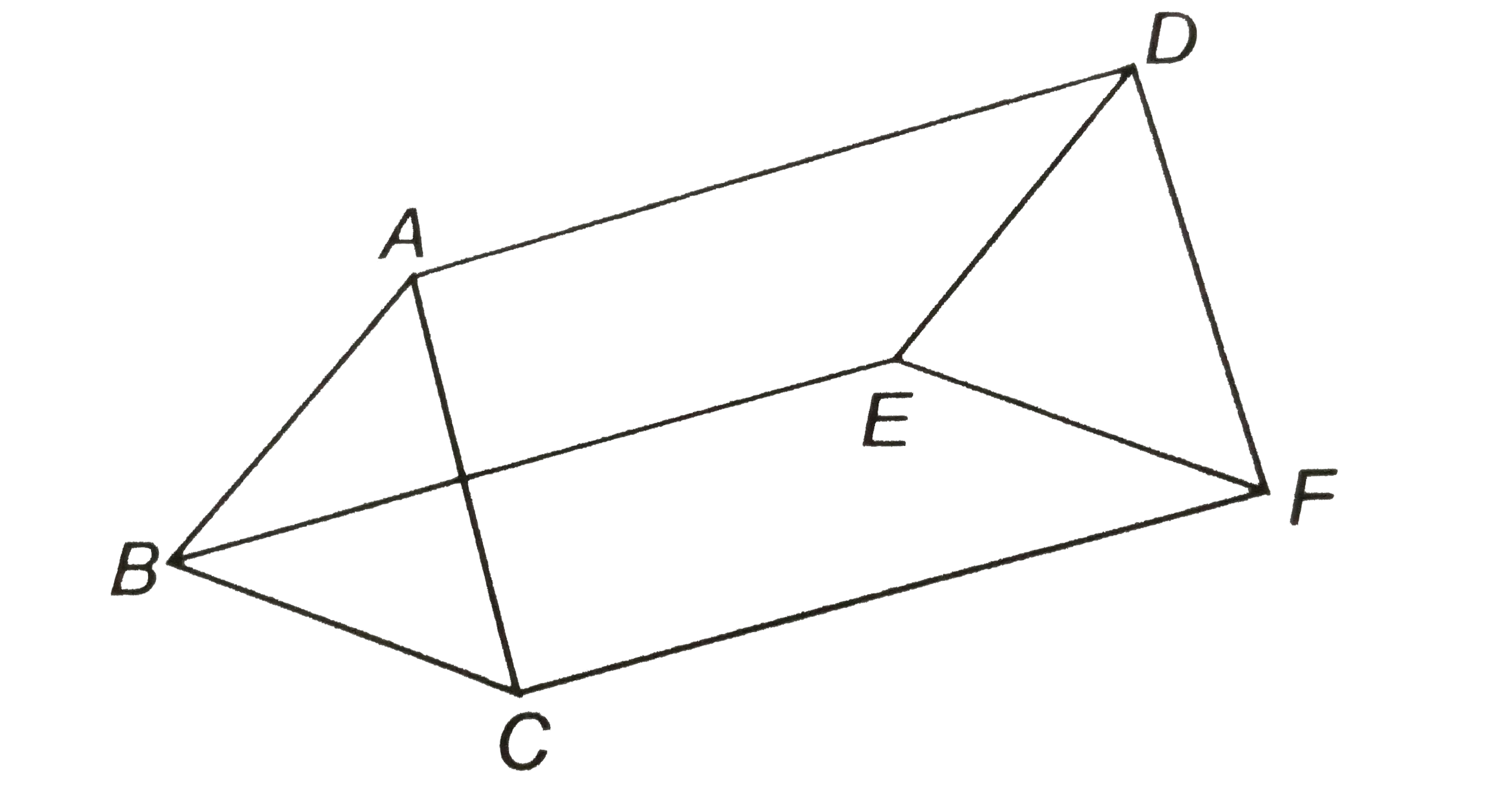
View SolutionIn figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
View Solution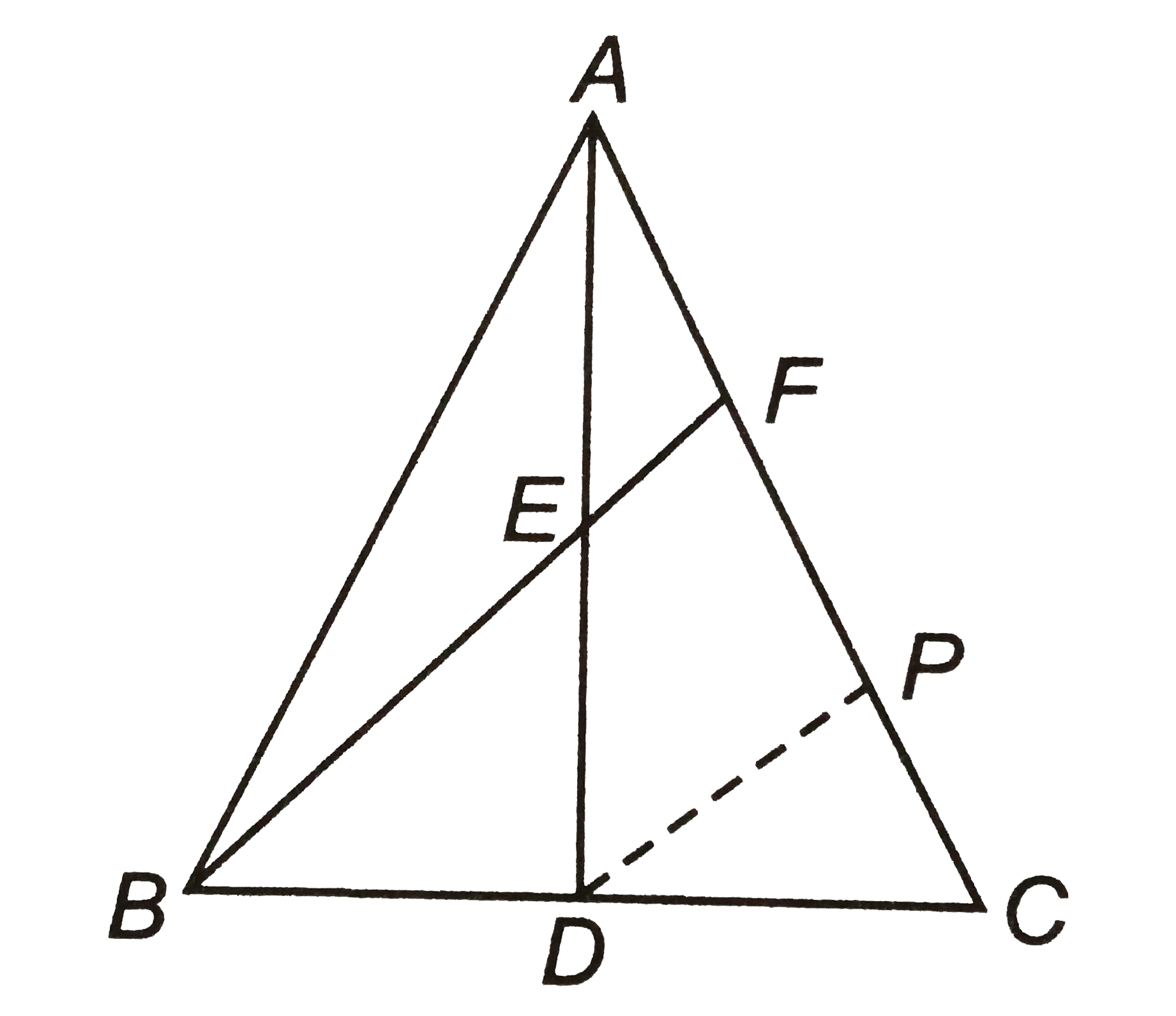 In ` A B C ,A D` is the median through `A` and `E` is the mid-point of `A D`. `B E` produced meets `A C` in `F` (Figure). Prove that `A F=1/3A Cdot`
In ` A B C ,A D` is the median through `A` and `E` is the mid-point of `A D`. `B E` produced meets `A C` in `F` (Figure). Prove that `A F=1/3A Cdot`
View SolutionThe quadrilateral, formed by joining the mid-points of the sides of a square, is a
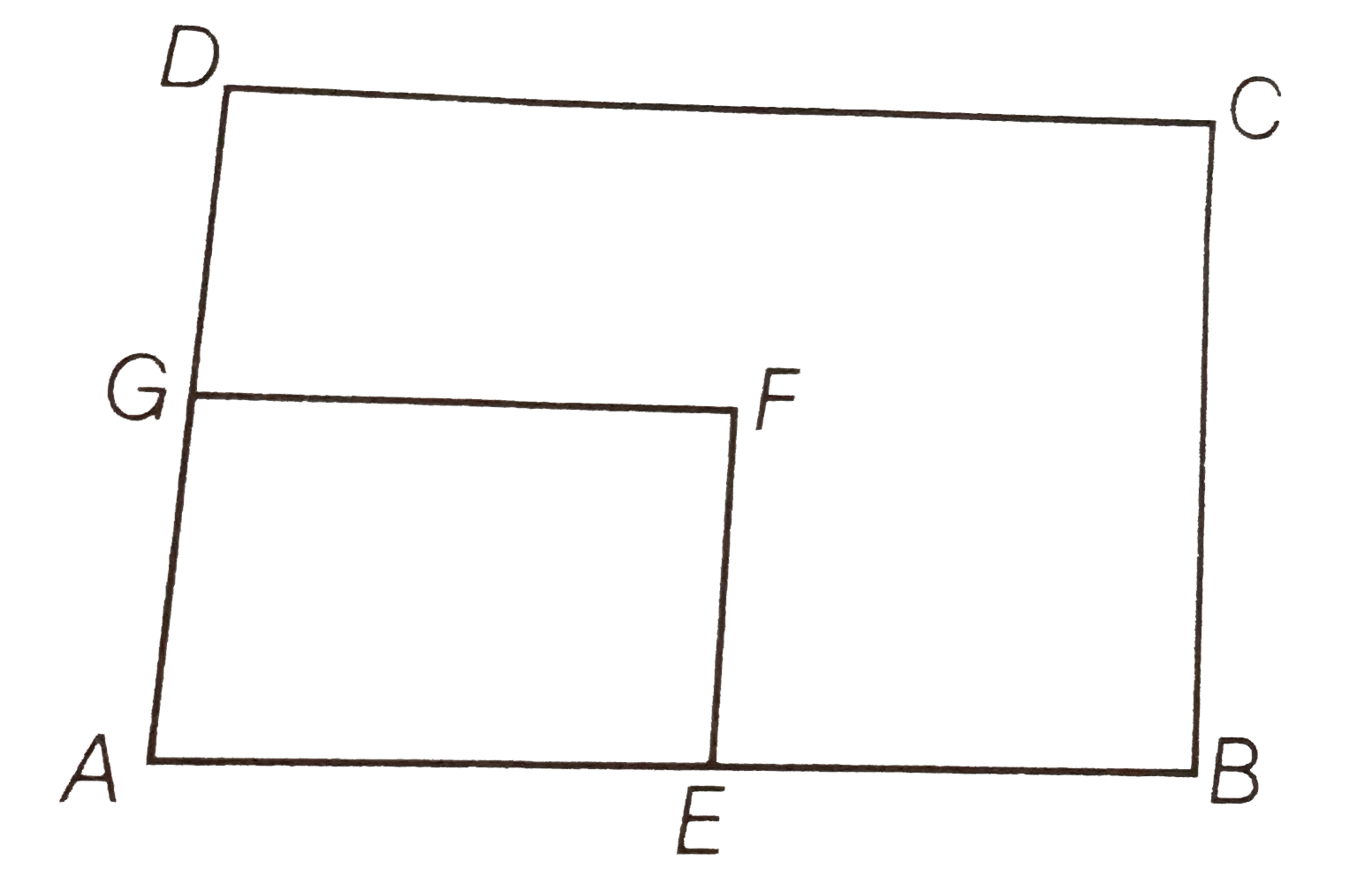
View SolutionIn Figure, `A B C D` isa trapezium in which side `A B` is a parallel to side `D C` and `E` is the mid-point of side `A Ddot` If `F` is a point on the side `B C` such that the segment `E F` is parallel to side `D C` . Prove that `F` is the mid point of `B C` and `E F=1/2(A B+D C)dot`
View SolutionThe quadrilateral formed by the bisectors of the angles of a parallelogram is a

View SolutionP and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View SolutionABCD is a rectangle in which diagonal BD bisects `angle B`. then `ABCD` is a
View SolutionIn `DeltaA B C`, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that `DeltaA B C`is divided into four congruent triangles by joining D, E and F.
View SolutionProve that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half the difference of these sides.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View Solution
Quadrilaterals questions and complete solutions for chapter QUADRILATERALS of NCERT MATHS (HINGLISH) of Class 9