Complete Solutions to प्रश्नावली 7.3 of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| MADHUR GUPTA | प्रश्नावली 7.3 |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
`DeltaABC" और "DeltaDBC` एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि :
(i) `DeltaABD~=DeltaACD`
(ii) `DeltaABP~=DeltaACP`
(iii) AP, कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

View SolutionAD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलाम्ब है, जिसमे AB = AC है। दर्शाइए कि :
(i) AD रेखाखण्ड BC को सद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।
View Solutionएक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM और PN क्रमशः एक-दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर है (देखिए आकृति) दर्शाइए कि :
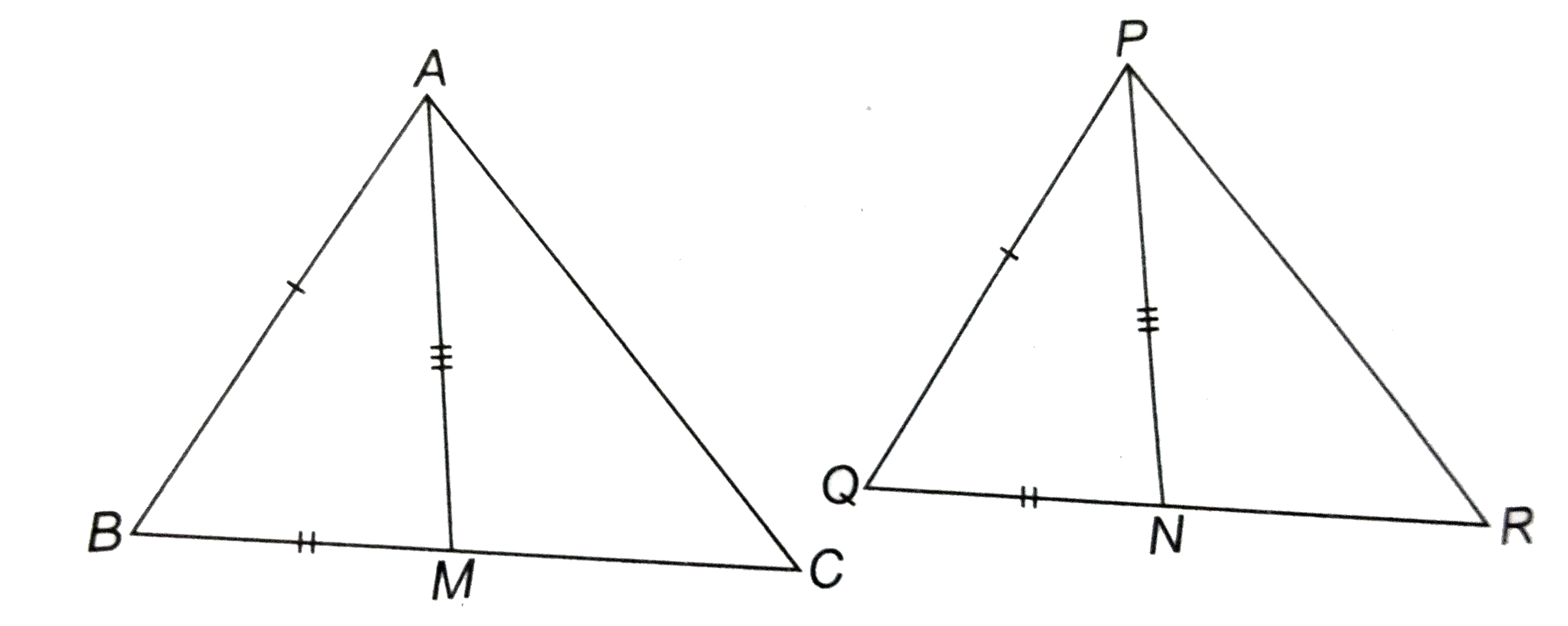
(i) `DeltaABM~=DeltaPQN`
(ii) `DeltaABC~=DeltaPQR`
View SolutionBE और CF एक त्रिभुज ABC के दो बराबर शीर्षलाम्ब है। R.H.S. सर्वागसमता नियम का प्रयोग करके सिद्ध कीजिए कि `DeltaABC` एक समद्विबाहु त्रिभुज है।
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमे AB=AC है। `APbotBC` खींच कर दर्शाइए कि `angleB=angleC` है।
View Solution
प्रश्नावली 7.3 questions and complete solutions for chapter त्रिभुज of NAGEEN MATHS (HINDI) of Class 9