Complete Solutions to उदाहरण of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| MADHUR GUPTA | उदाहरण |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
दिए चित्र में सिद्ध कीजिए कि AC = BD
View Solutionसंलग्न चित्र में, AB =CD तथा `AB||CD` है। सिद्ध कीजिए कि :
(i) `DeltaAOB~=DeltaDOC`
(ii) ACऔर BD एक-दूसरे को बिन्दु O पर समद्विभाजित करते है।
View Solution`DeltaABC` की भुजाएँ AB और BC और माध्यिका AD क्रमशः `DeltaPQR` की भुजाओं PQ और QR माध्यिका PM के बराबर है। सिद्ध कीजिए कि त्रिभुज ABC और PQR सर्वांगसम है।
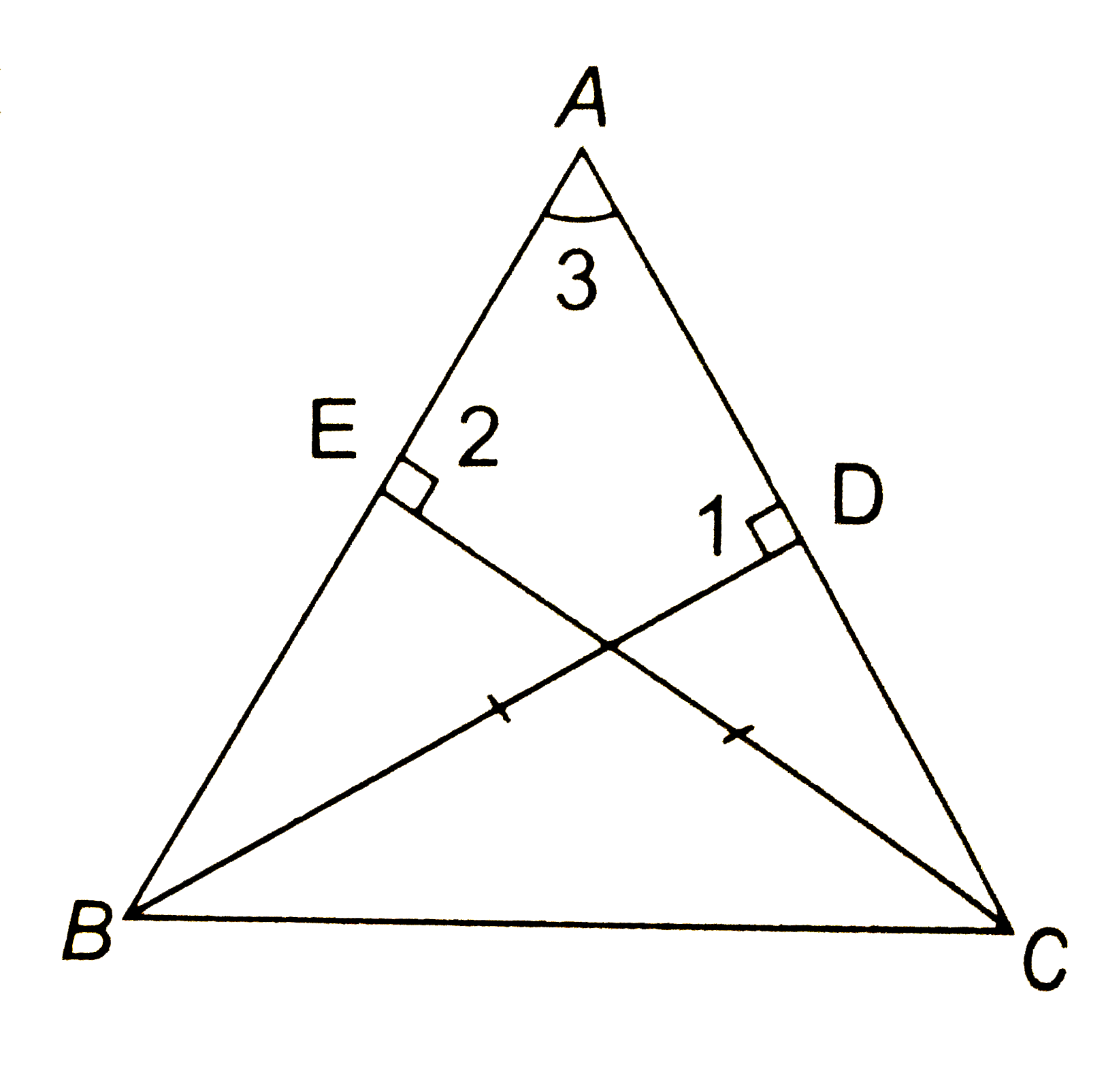
View Solutionसंलग्न चित्र में, BD = CE और `angleADB=angleAEC=90^(@)` है, सिद्ध कीजिए कि :
(i) `DeltaABD~=DeltaACE` (ii) ABC एक समद्विबाहु त्रिभुज है।
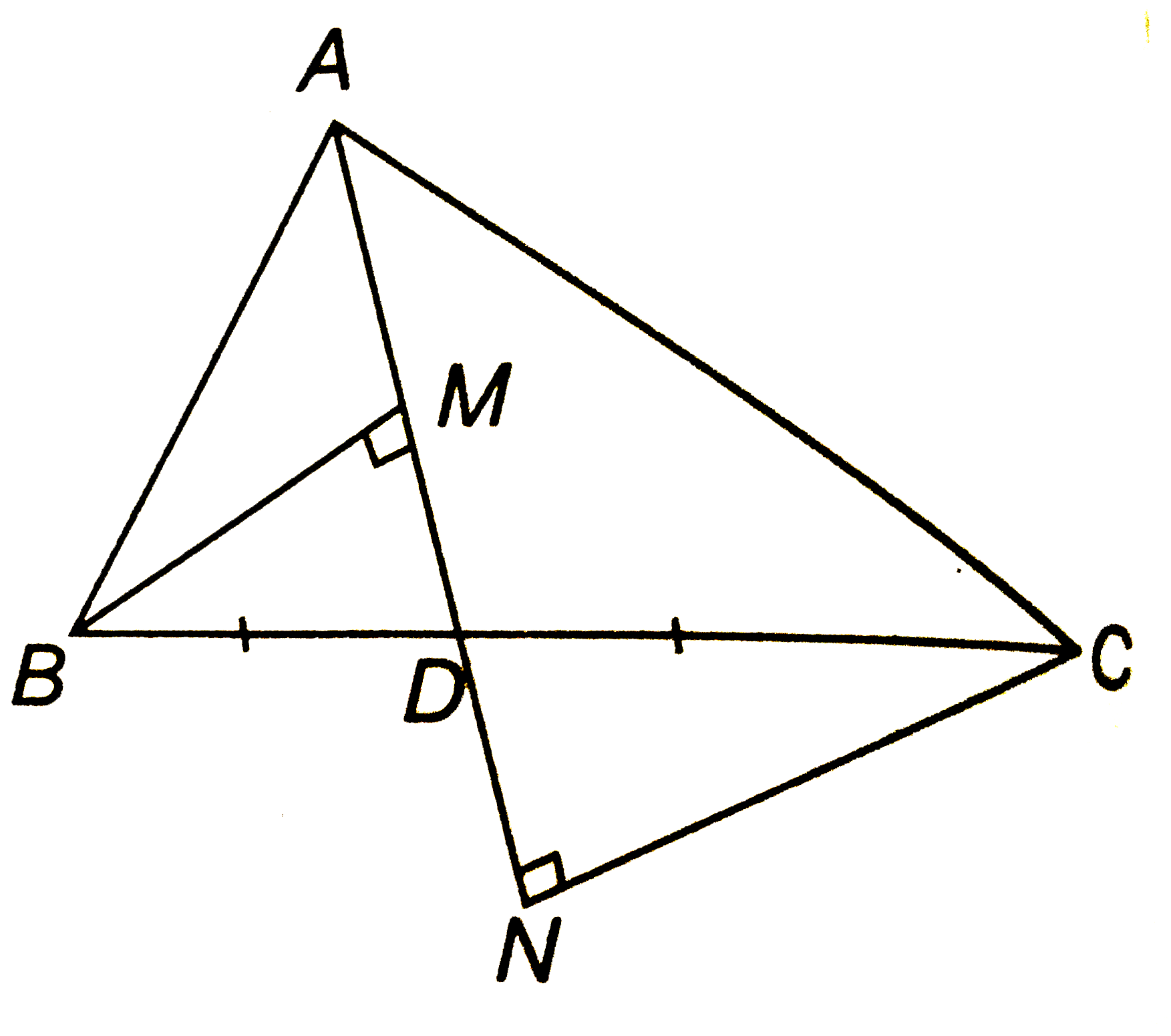
View Solutionसंलग्न चित्र में, D भुजा BC का माध्य-बिन्दु है। यदि BM और CN क्रमशः B और C से AD और बढ़ाई गई AD पर लम्ब है, तो सिद्ध कीजिए कि
BM=CN
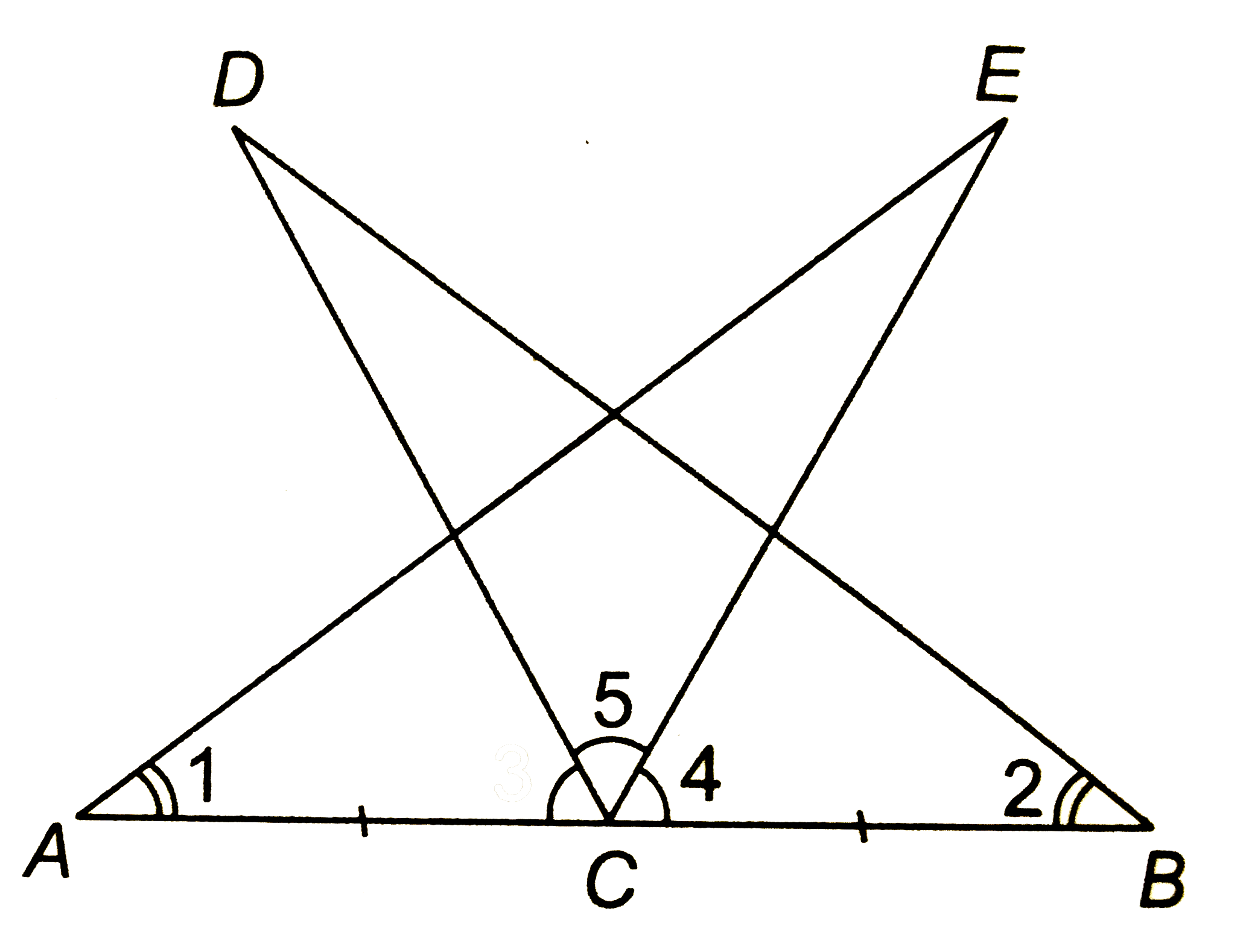
View SolutionAC = BC,`angleDCA`= `angleECB` ,`angleDBC` =` angleEAC`
दी सूचनाओं का प्रयोग करके सिद्ध कीजिए कि :
(i) `DeltaEAC~=DeltaDBC` (ii) EC=DC
दो त्रिभुजों को सर्वांगसम सिद्ध करने में प्रयुक्त युकिल्ड के अभिगृहित को भी बताइए।
View Solutionसंलग्न चित्र में, ABCD एक समान्तर चतुर्भुज है, ABM एक रेखा खण्ड है और E, BC का माध्य-बिन्दु है। सिद्ध कीजिए कि :
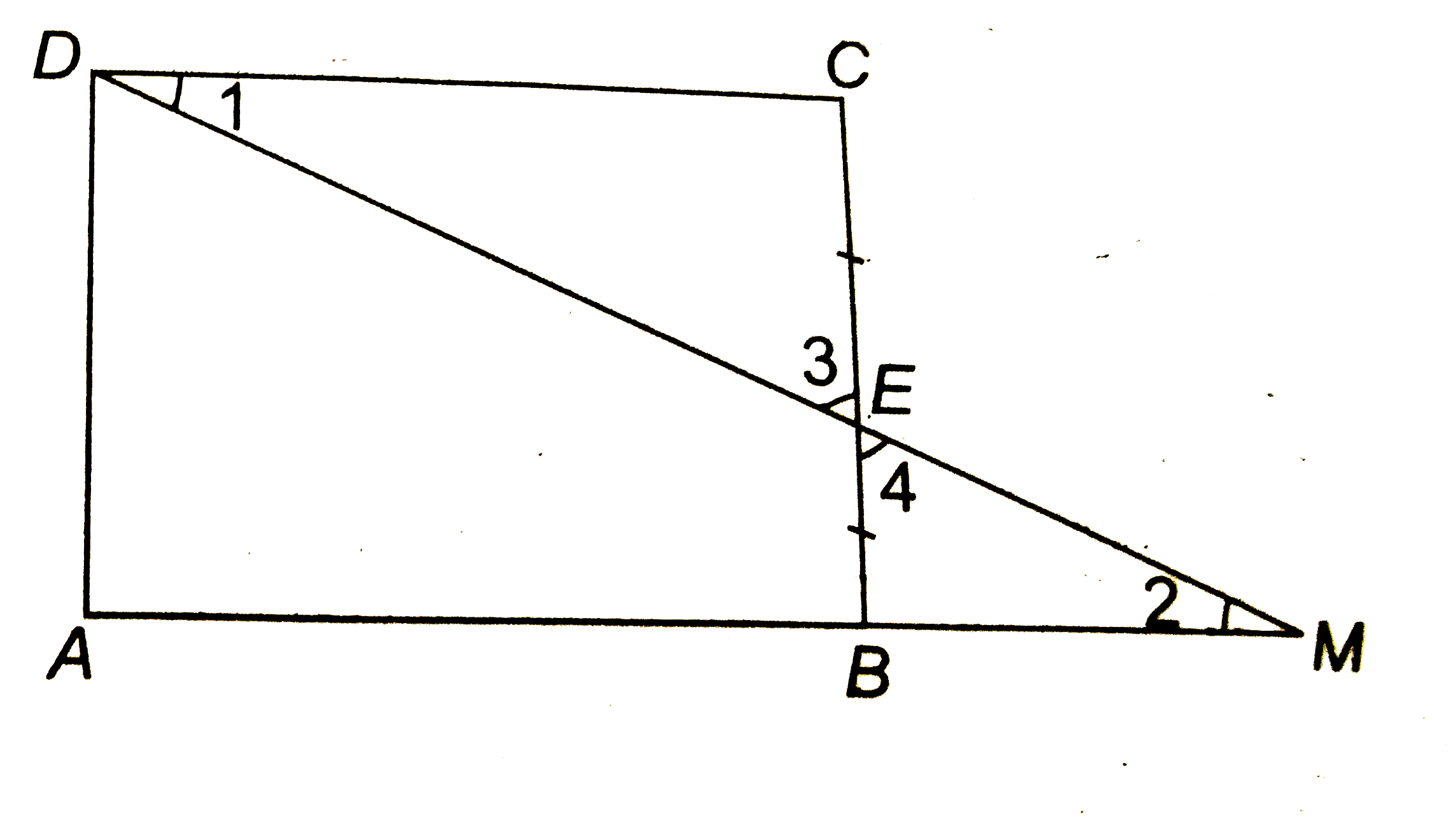
(i) `DeltaDCE~=DeltaMBE`
(ii) AB=BM
(iii) AM=2DC
View Solutionदी आकृति में, `DeltaABC` के आधार BC पर बिन्दु D और E इस प्रकार है कि BD=CE, AD=AE और `angleADE=angleAED` है। सिद्ध कीजिए कि `DeltaADB~=DeltaAEC`.
View Solutionदी आकृति में, PS=PR, `angleTPS=angleQPR` है। सिद्ध कीजिए कि PT=PQ.
View SolutionBE और CF, `DeltaABC` के दो बराबर लम्ब है। R.H.S. सर्वागसमता निगम का प्रयोग करके दिखाइए कि `DeltaABC` समद्विबाहु है।
View Solutionसंलग्न चित्र में, `angleFEB` की माप ज्ञात कीजिए यदि भुजाओं AD, DF और FE की लम्बाइयाँ समान है और `angleACB=65^(@)` है।
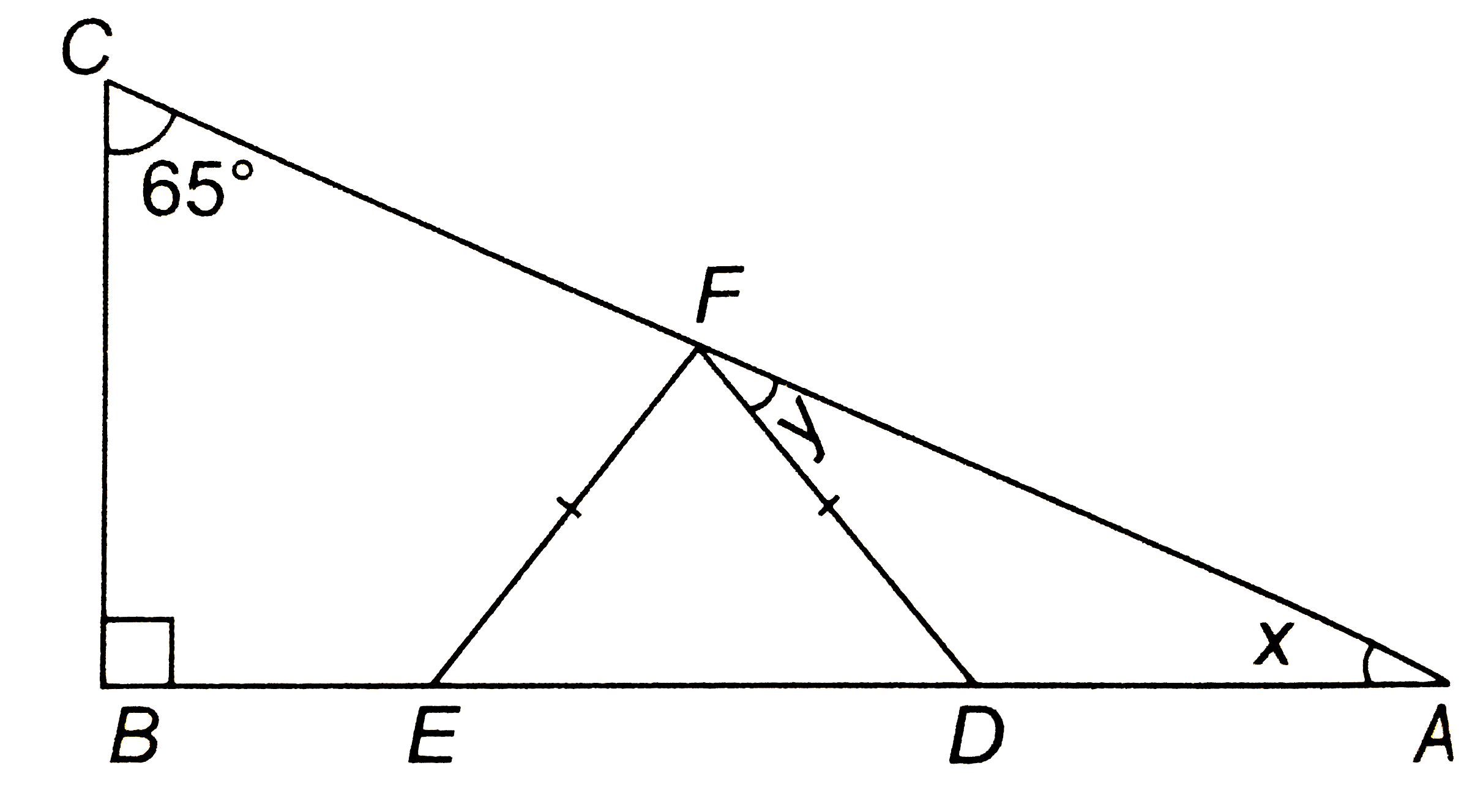
View Solutionएक त्रिभुज ABC में, `angleB=2angleC` है। BC पर एक बिन्दु D इस प्रकार है कि AD, `angleBAC` को समद्विभाजित करता है और AB =CD है। सिद्ध कीजिए कि `angleBAC=72^(@)`
View Solution
उदाहरण questions and complete solutions for chapter त्रिभुज of NAGEEN MATHS (HINDI) of Class 9