Complete Solutions to प्रश्नावली 7A of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| MADHUR GUPTA | प्रश्नावली 7A |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
निम्नलिखित में से कौन-से त्रिभुजों के युग्म सर्वांगसम है ? प्रत्येक में सर्वागसमता का प्रतिबन्ध भी बताइए :
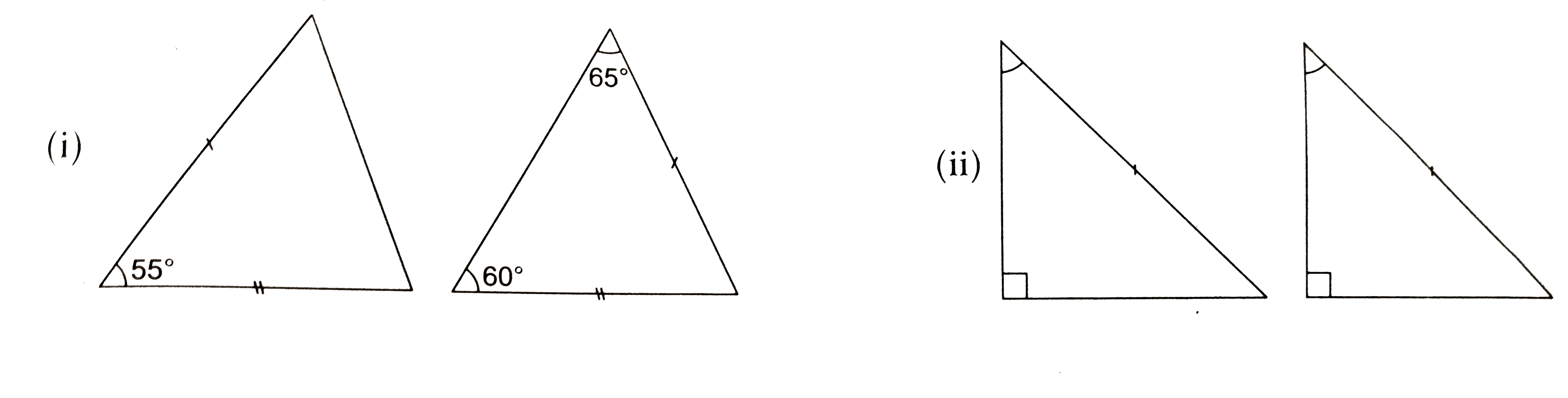
View Solution`DeltaABC` में, D, BC का माध्य-बिन्दु, है। AD को E तक इस प्रकार बढ़ाया गया है कि DE =AD है। सिद्ध कीजिए कि :
(i) `DeltaABD" और "DeltaECD` सर्वांगसम है, (ii) AB=EC (iii) AB और EC समान्तर है।
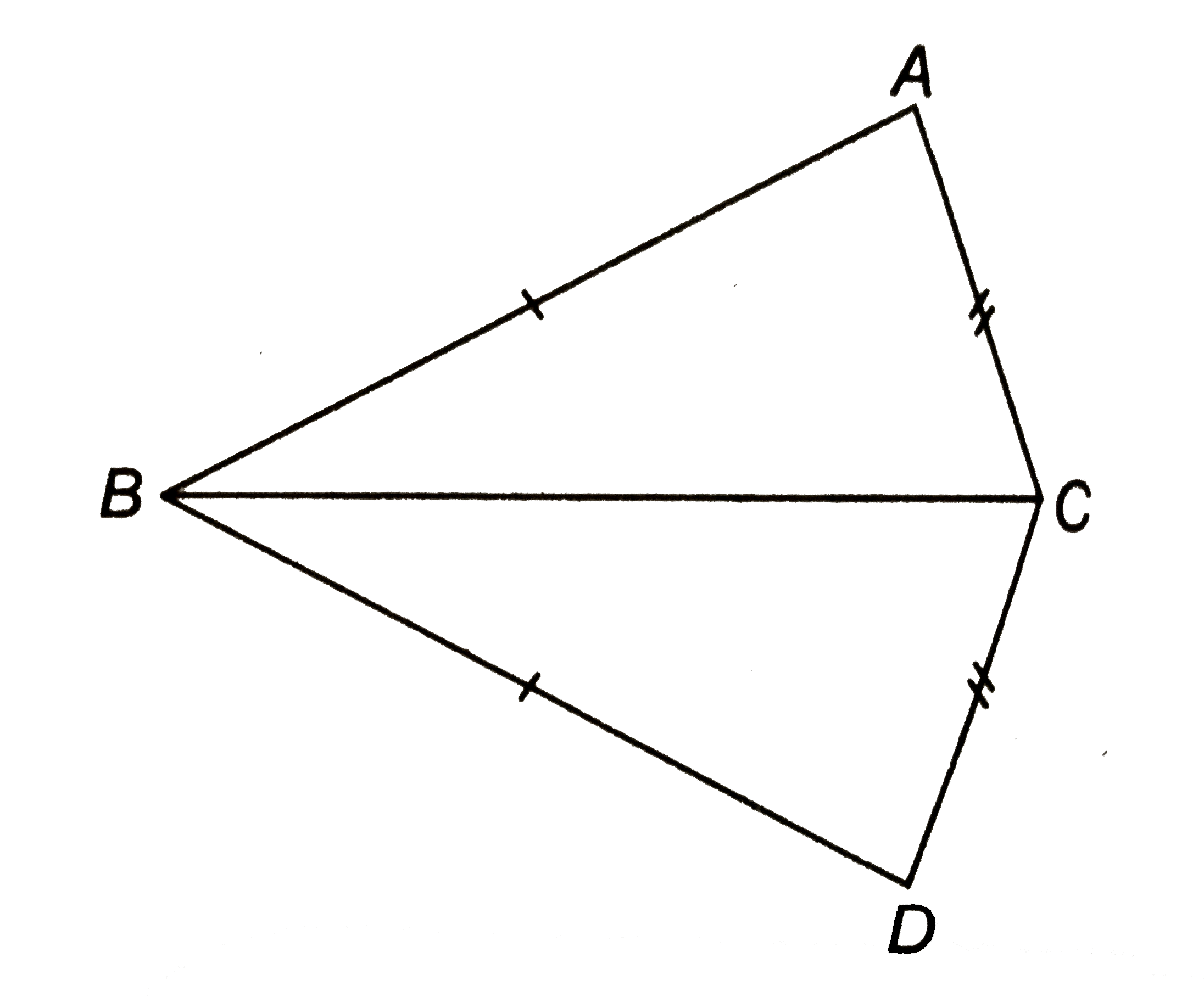
View Solutionदी आकृति में, AB =DB और AC =DC है। यदि `angleABD=58^(@),angleDBC=2x-4^(@),angleACB=y+15^(@)" और "angleDCB=63^(@)` है, तो x और y के मान ज्ञात कीजिए।
View SolutionBD, `angleABC` की समद्विभाजक है। BD पर स्थित एक बिन्दु P से AB और BC पर लम्ब क्रमशः PE और PF डाले गये है। सिद्ध कीजिए कि :
(i) `DeltaBEP~=DeltaACD` (ii) PE=PF.
View Solution`DeltaABD` में, AB=AD और AC,BD को समद्विभाजित करती है। सिद्ध कीजिए कि `DeltaABC~=DeltaADC`.
View Solution`DeltaABC` में, AB=AC और कोण A का समद्विभाजक BC को D पर मिलता है। सिद्ध कीजिए कि :
(i) `DeltaABD~=DeltaACD` (ii) AD, BC पर लम्ब है।
View Solutionचतुर्भुज ABCD में, AB =DC और AD =BC है। सिद्ध कीजिए कि AB और DC एक-दूसरे के समान्तर है।
View Solution`DeltaABC` में, AB=AC तथा `angleB" और "angleC` को समद्विभाजक क्रमशः AC और AB को बिन्दुओं D और E पर मिलते है। सिद्ध कीजिए कि BD =CE .
View Solution`DeltaABC" में, "angleB=angleC` है। सिद्ध कीजिए कि BC के माध्य-बिन्दु से AB और AC पर डाले गये लम्ब बराबर है।
View Solutionनिम्नलिखित प्रत्येक चित्र में दो सर्वांगसम त्रिभुज दिखाए गये है। प्रत्येक से x और y के मान ज्ञात कीजिए :
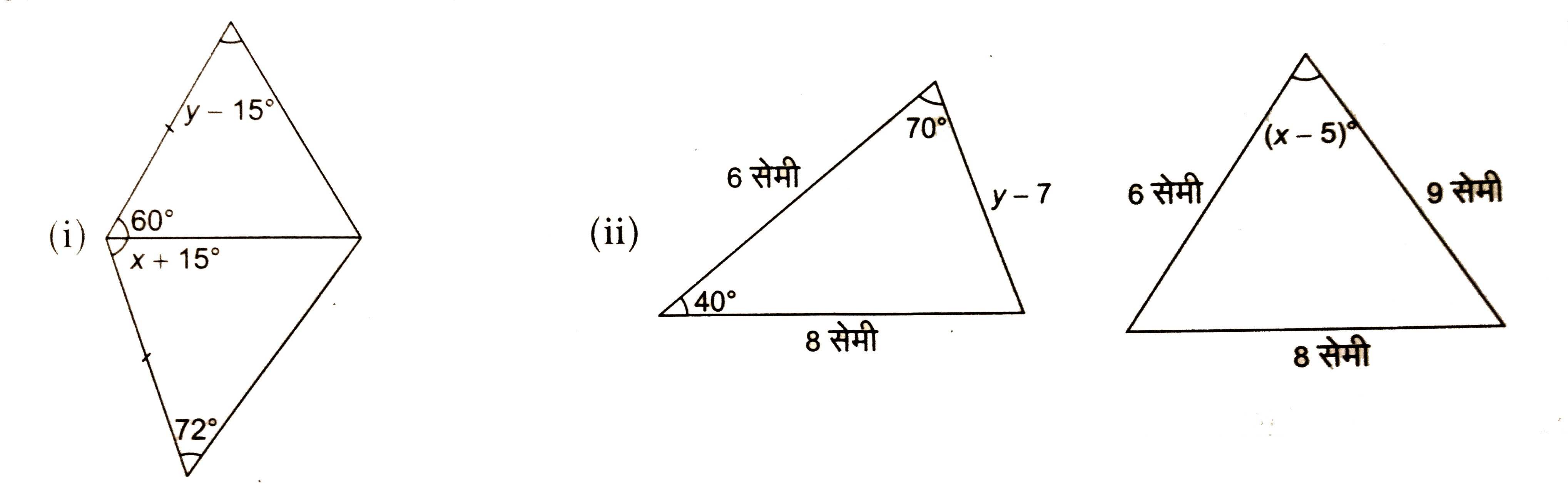
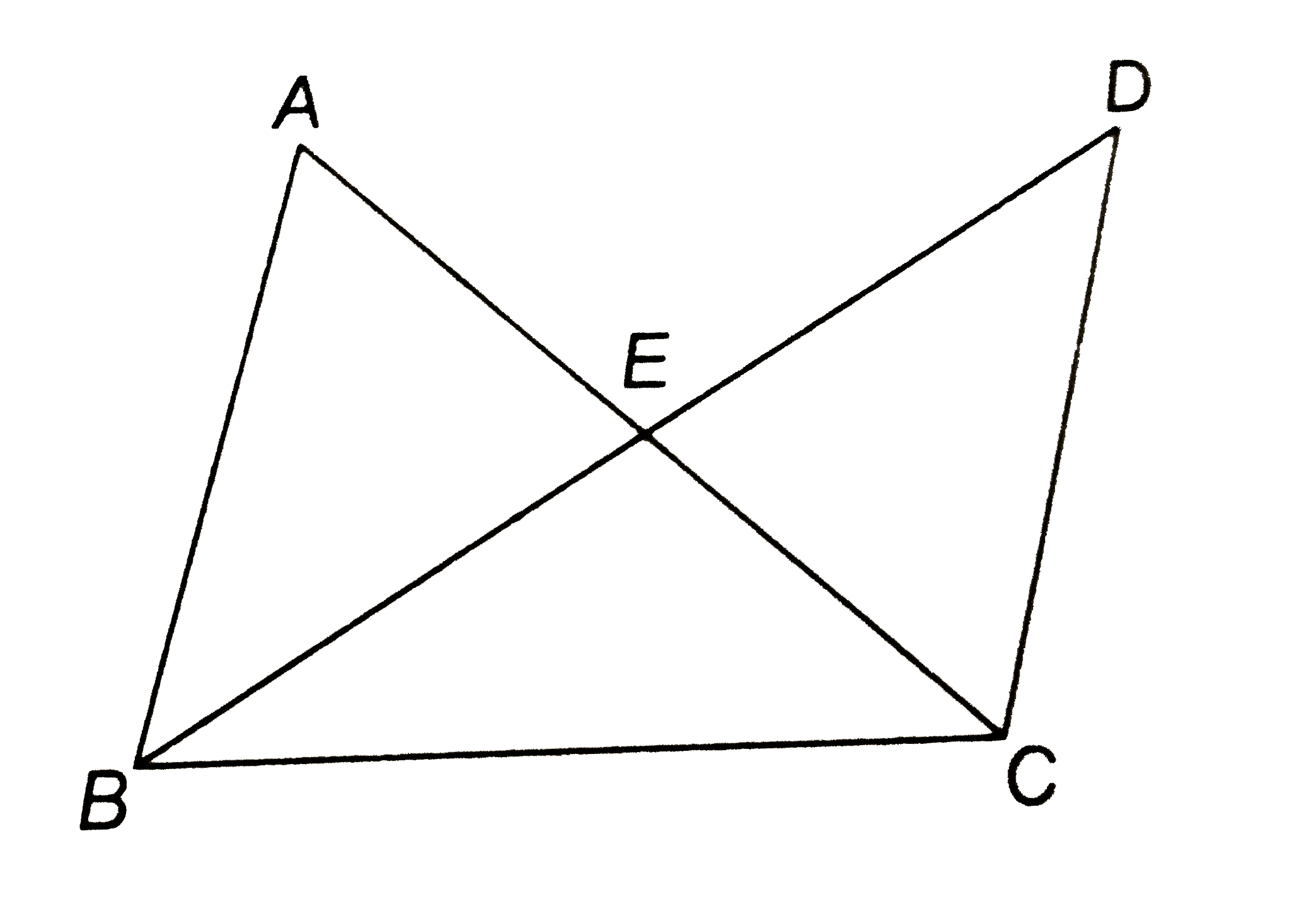
View Solutionसंलग्न चित्र में, `angleBAC=angleBDC" और "angleABC=angleBCD` है। सिद्ध कीजिए कि :
(i) `DeltaABC~=DeltaDCB`
(ii) `DeltaABE~=DeltaDCF`
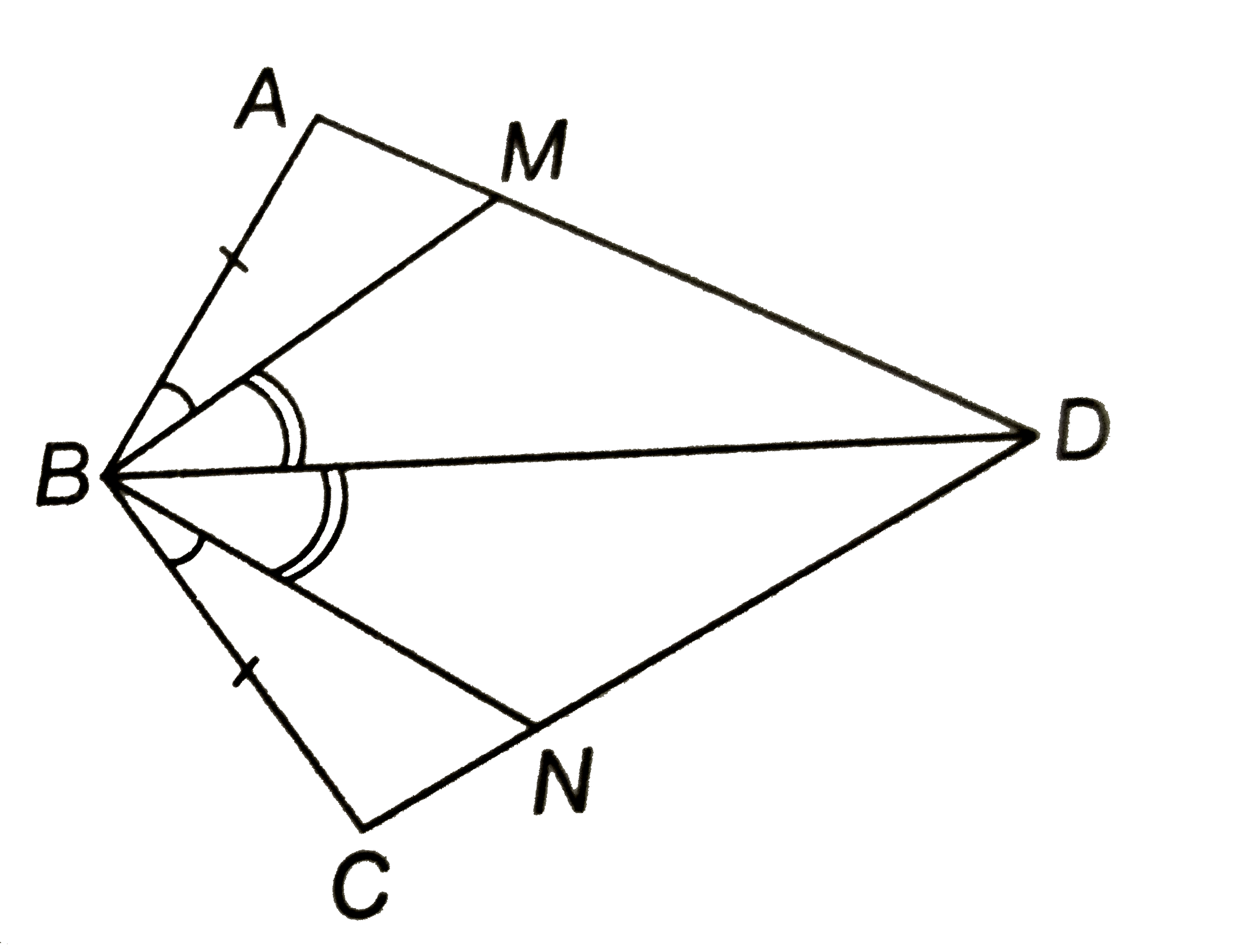
View Solutionसंग्लन चित्र में, ABCD एक चतुर्भज है। M और N क्रमशः AB और CD पर स्थित बिन्दु इस प्रकार है कि `AB=BC,angleABM=angleCBN" और "angleMBD=angleNBD` है। सिद्ध कीजिए कि BM=BN.
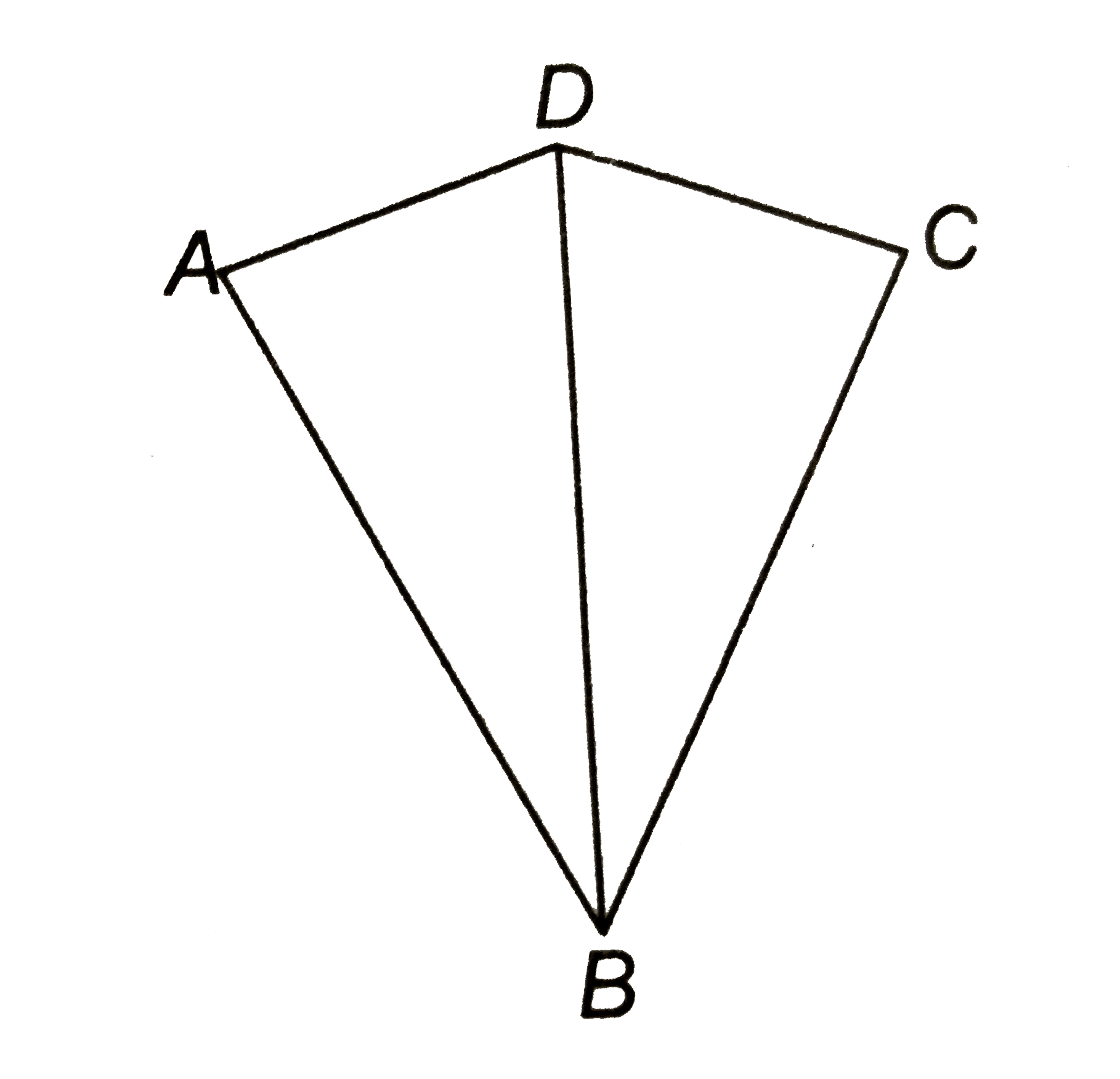
View Solutionदिया है AD = DC और DB, `angleADC` को समद्विभाजित करता है।
(i) सिद्ध कीजिए कि `DeltaADB~=DeltaCDB`
(ii) यदि `angleABD=48^(@)," तो, "angleCBD` ज्ञात कीजिए।
View Solutionसंलग्न चित्र में, एक वर्ग ABCD और एक समबाहु त्रिभुज DEC दर्शाए गये है। सिद्ध कीजिए कि :
(i) `angleADE=angleBCE=30^(@)`
(ii) `DeltaADE~=DeltaBCE`

View Solution`DeltaABC` की भुजाओं AB और AC पर बाहर की ओर क्रमशः समबाहु `DeltaABD` और समबाहु `DeltaACE` बनाये गये है। सिद्ध कीजिए कि :
(i) `angleDAC=angleEAB` (ii) DC=BE
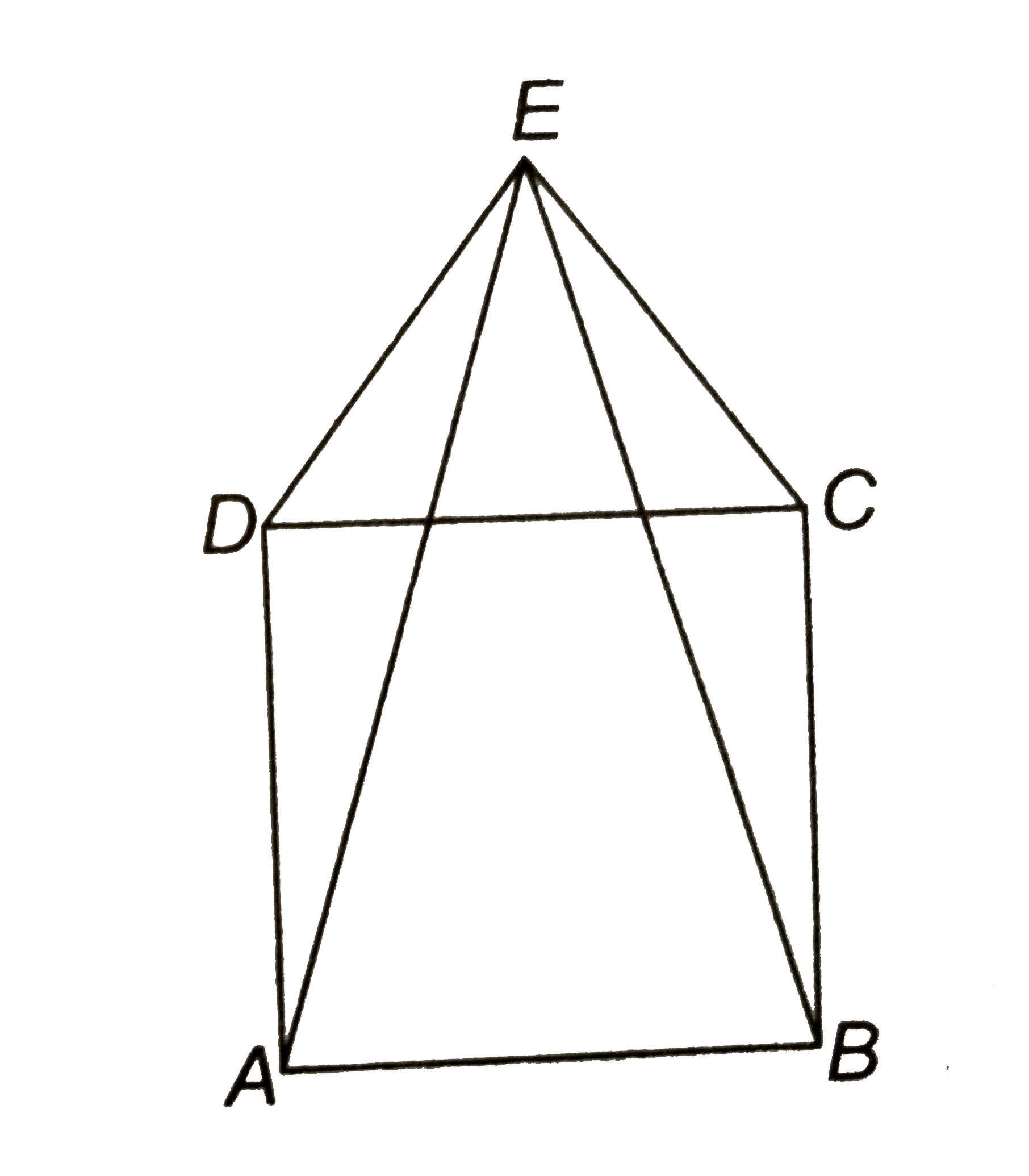
View Solutionसंलग्न चित्र में, एक वर्ग ABCD और एक समबाहु त्रिभुज DCE दर्शाए गये है। सिद्ध कीजिए कि :
(i) `angleADE=angleBCE=150^(@)`
(ii) `DeltaADCE~=DeltaBCE`
(iii) AE=BE
View Solution`DeltaABC` में, BD भुजा AC की माध्यिका है, BD को E तक इस प्रकार बढ़ाया गया है कि BD = DE है। सिद्ध कीजिए कि AE, BC के समान्तर है।
View Solutionदी आकृति में, `angleBDC`=`angleBEA" और "AB=BC` है। दिखाइए कि AE=CD.
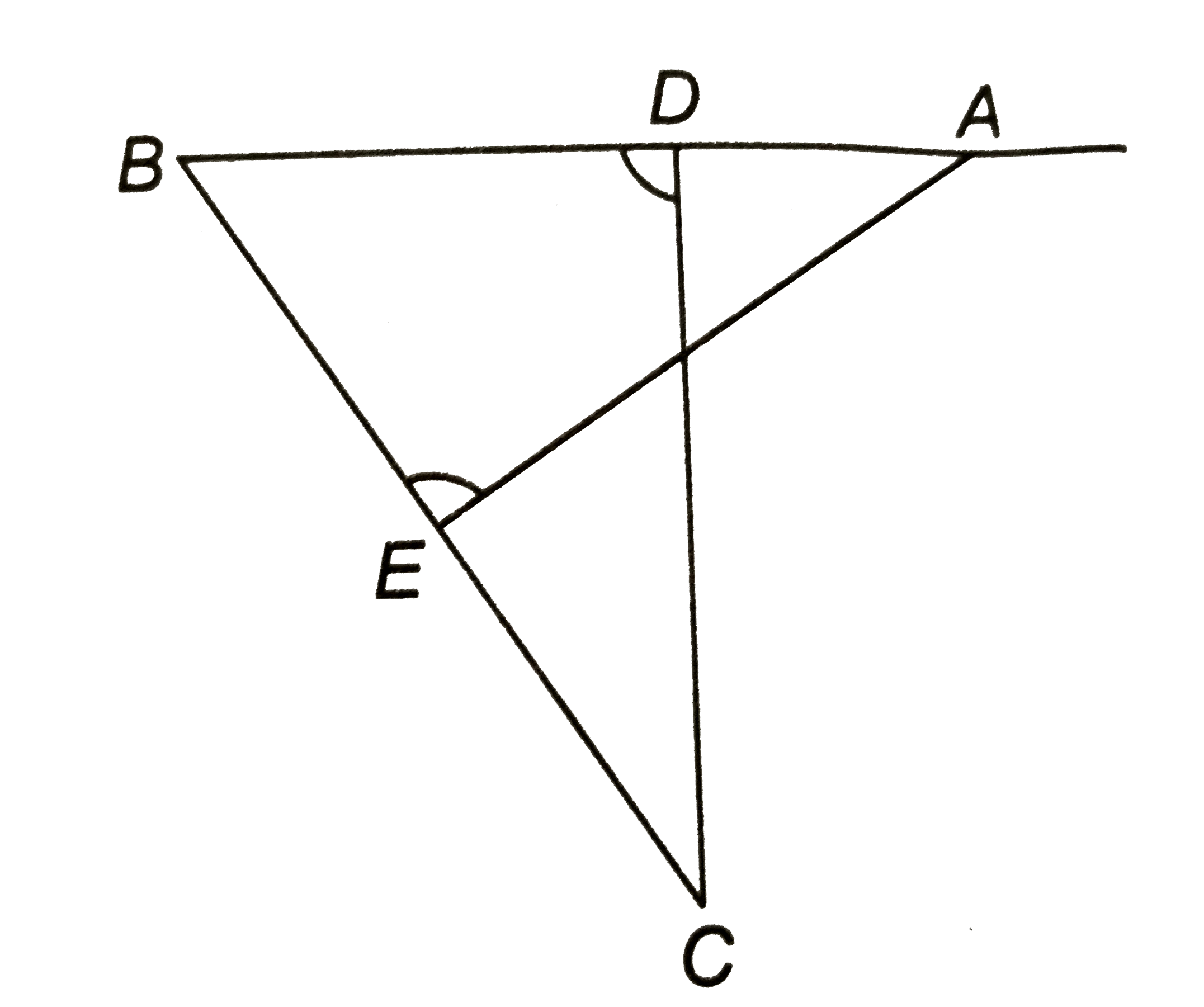
View Solutionयदि एक चतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते है, तो सिद्ध कीजिए कि वह एक समचतुर्भुज है।
View Solutionदी आकृति में, BM और DN क्रमशः B और D बिन्दुओं से AC पर लम्ब इस प्रकार है कि BM = DN है। सिद्ध कीजिए कि BO = OD .
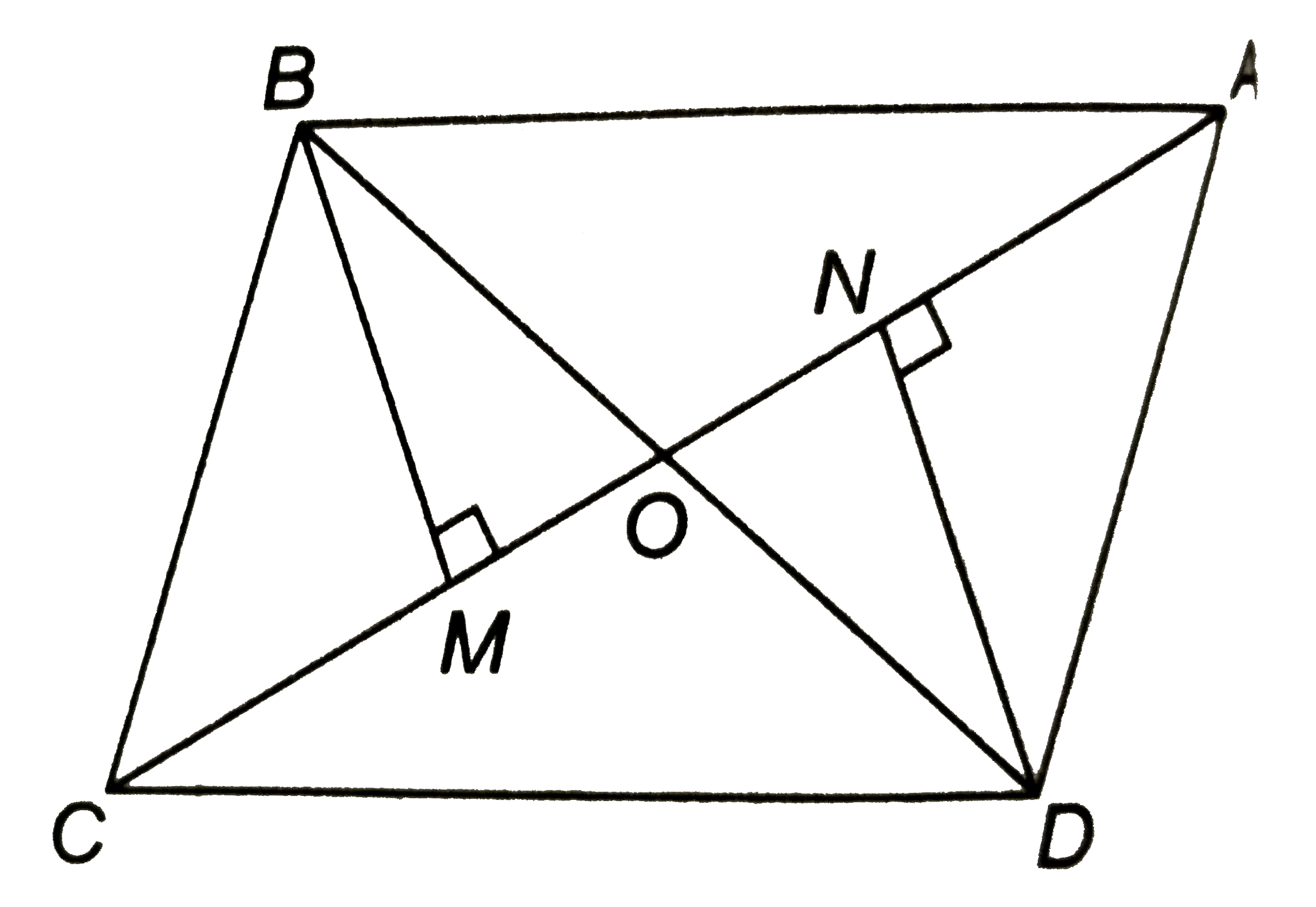
View Solutionसंलग्न चित्र में, `AB=EF,BC=DE,angleABC=angleFED=90^(@)` है। सिद्ध कीजिए कि AD = CF.

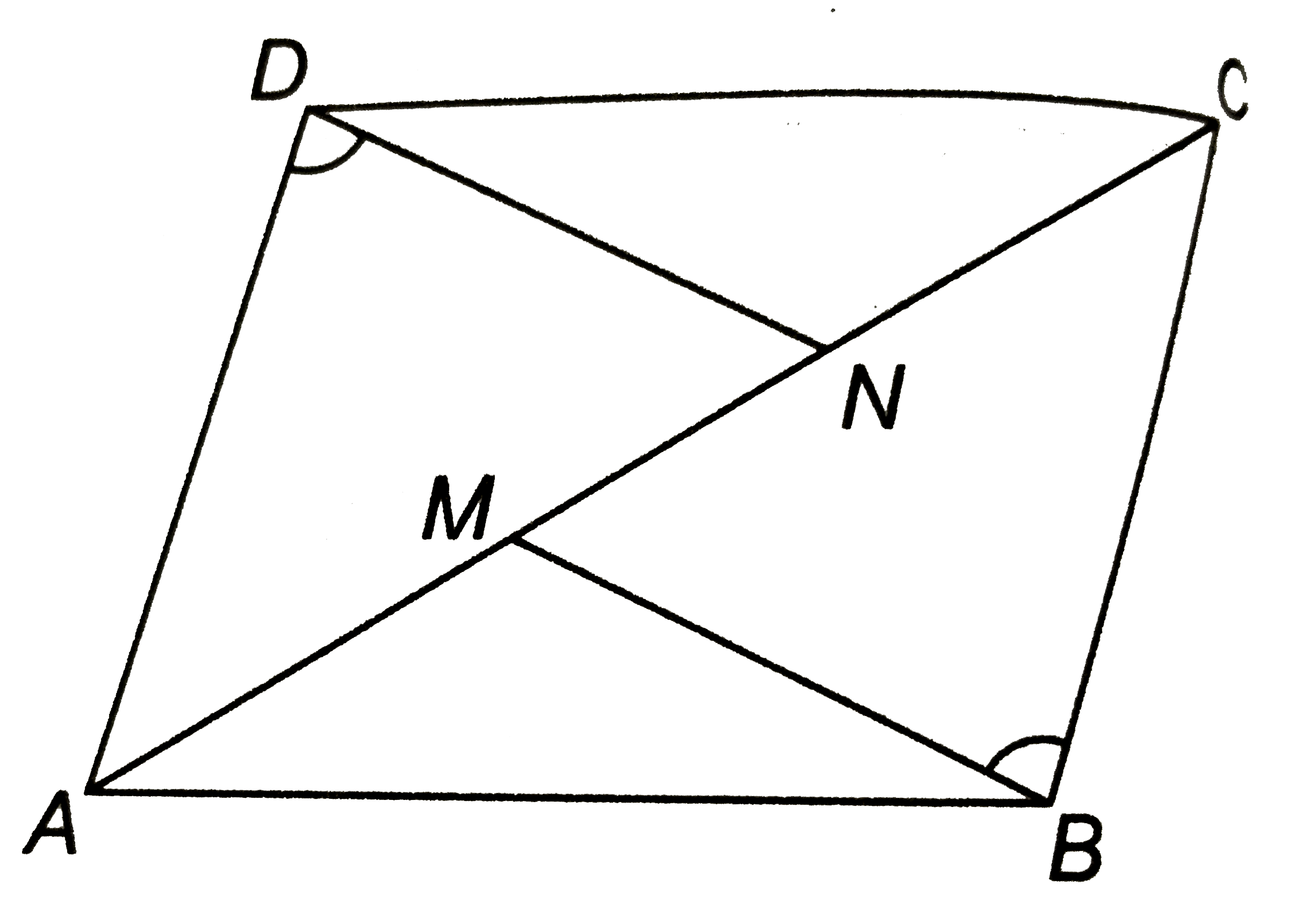
View Solutionसंलग्न चित्र में, ABCD एक समान्तर चतुर्भुज है। यदि `angleMBC=angleNDA`, तो सिद्ध कीजिए कि AM=NC.
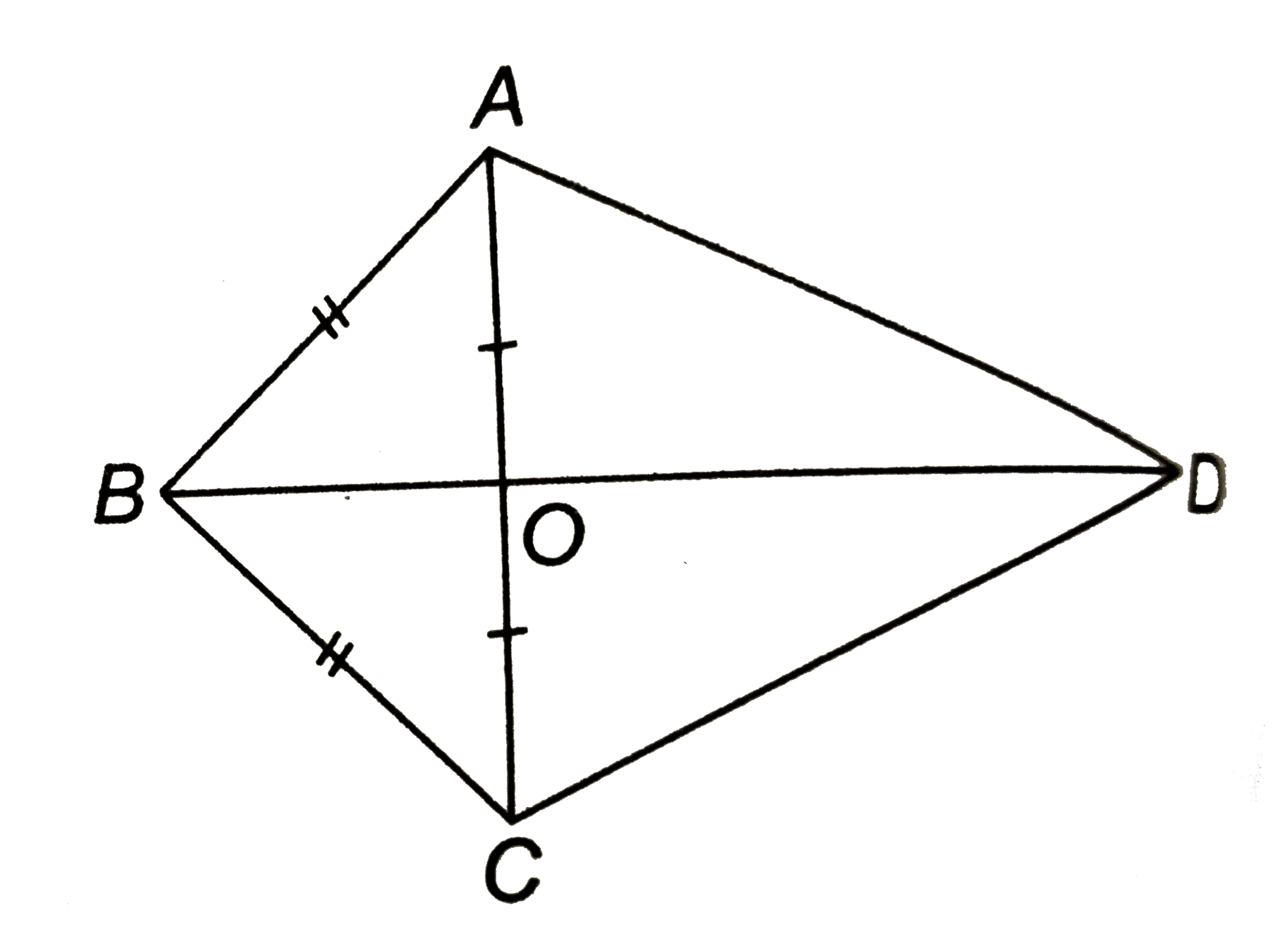
View Solutionदी आकृति में, OA = OC और AB =BC है। सिद्ध कीजिए कि :
(i) `angleAOB=90^(@)`
(ii) `DeltaAOD~=DeltaCOD`
(iii) AD=CD
View Solutionसंलग्न चित्र में, ABCD एक समान्तर चतुर्भुज है। यदि भुजा AB को P तक इस प्रकार बढ़ाया गया है कि AB =BP तथा भुजा AD को Q तक इस प्रकार बढ़ाया गया है कि AD =DQ , तो सिद्ध कीजिए कि CP=CQ.
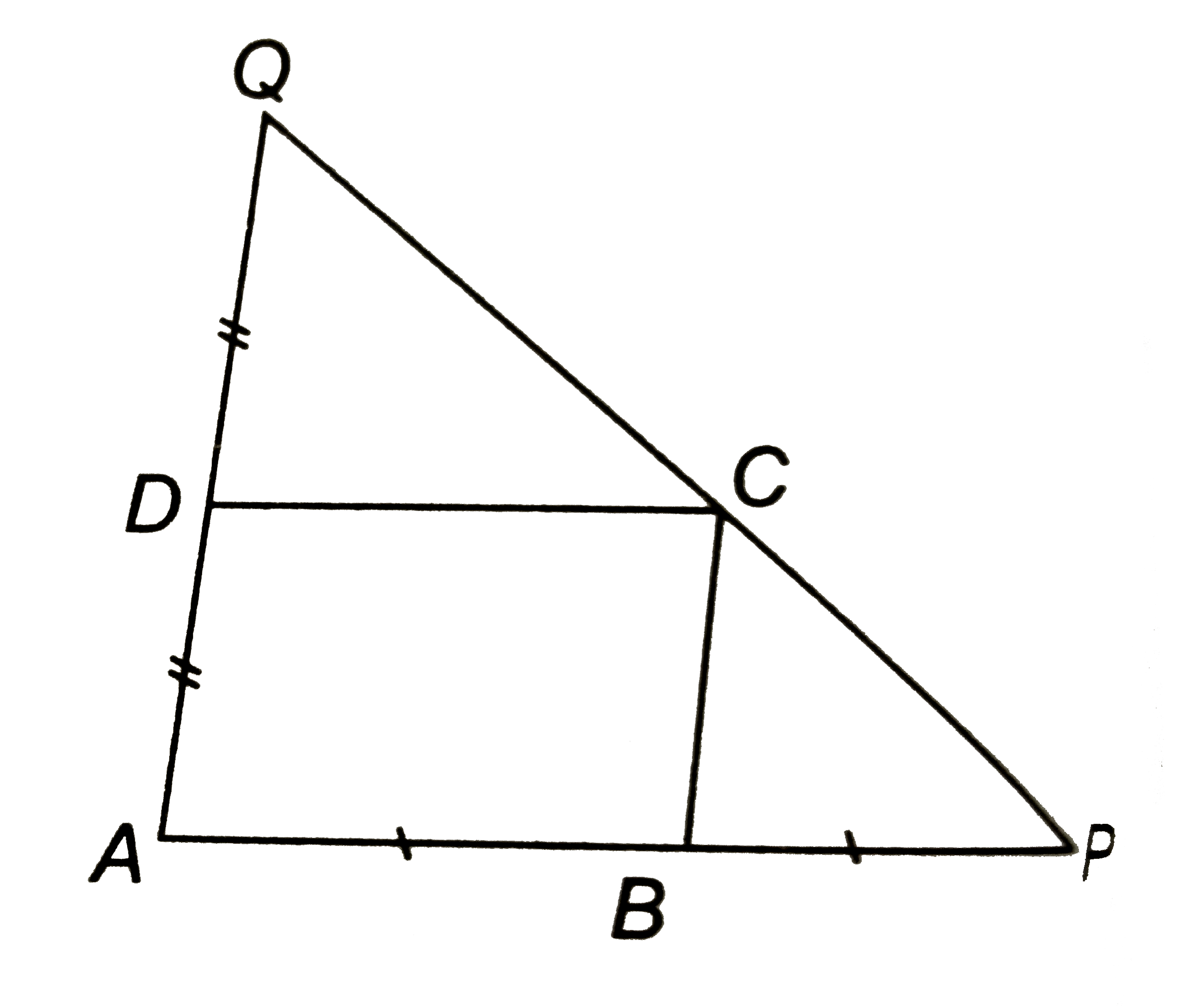
View Solutionनिम्नलिखित चित्र में, `AB=PQ,AC=PR" और "AM=PN` है। सिद्ध कीजिए कि `DeltaABC~=DeltaPQR`
View Solutionसिद्ध कीजिए कि एक समबाहु त्रिभुज कि माध्यिकाएँ बराबर होती है ।
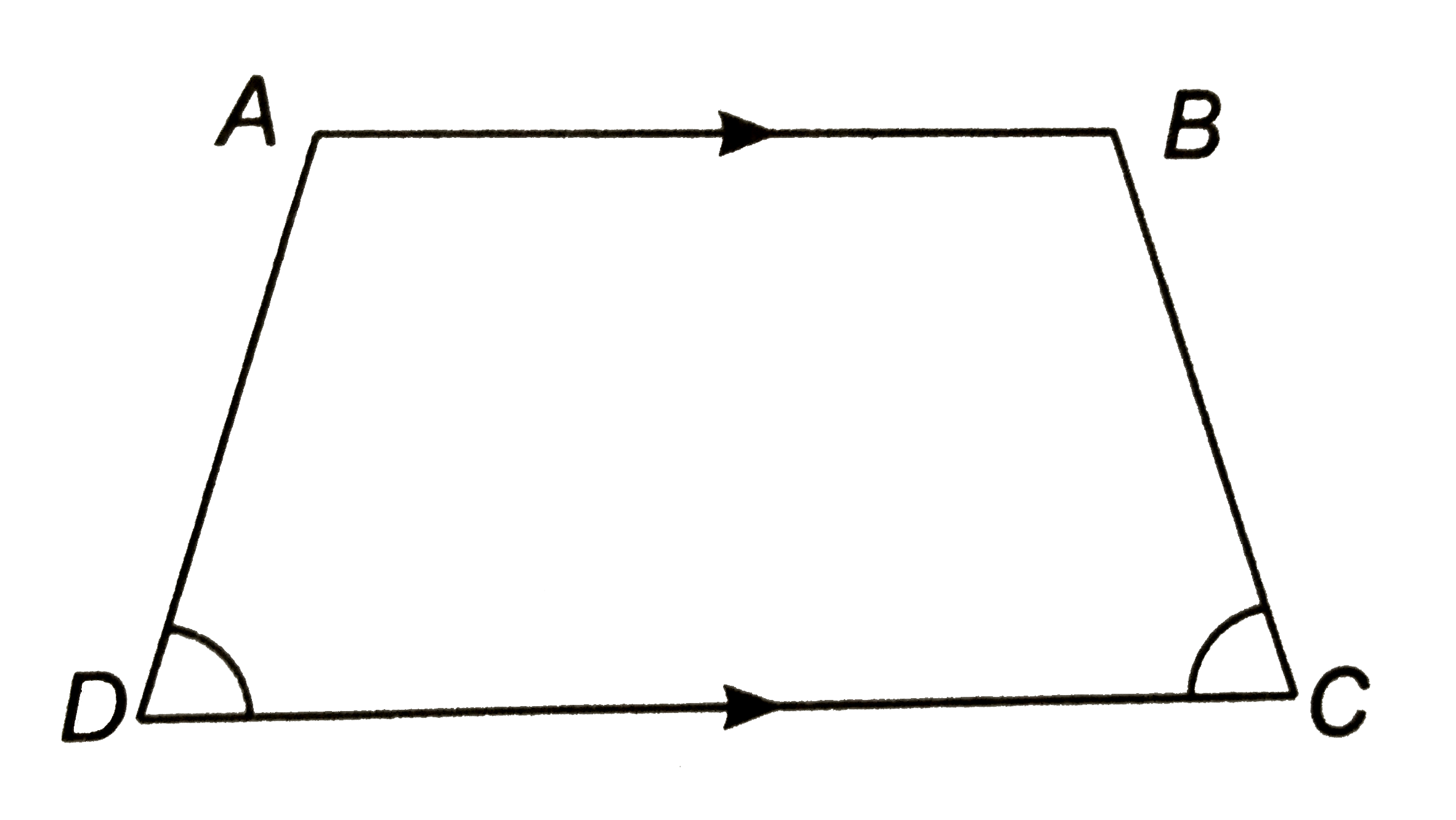
View Solutionदी आकृति में, `AB||DC` और `angleD=angleC` है। सिद्ध कीजिए कि :
(i) AD=BC
(ii) AC=BD
View Solutionदी आकृति में, `AB||FD,AC||GE" और "BD=CE`
है। सिद्ध कीजिए कि :
(i) BG=DF
CF=EG
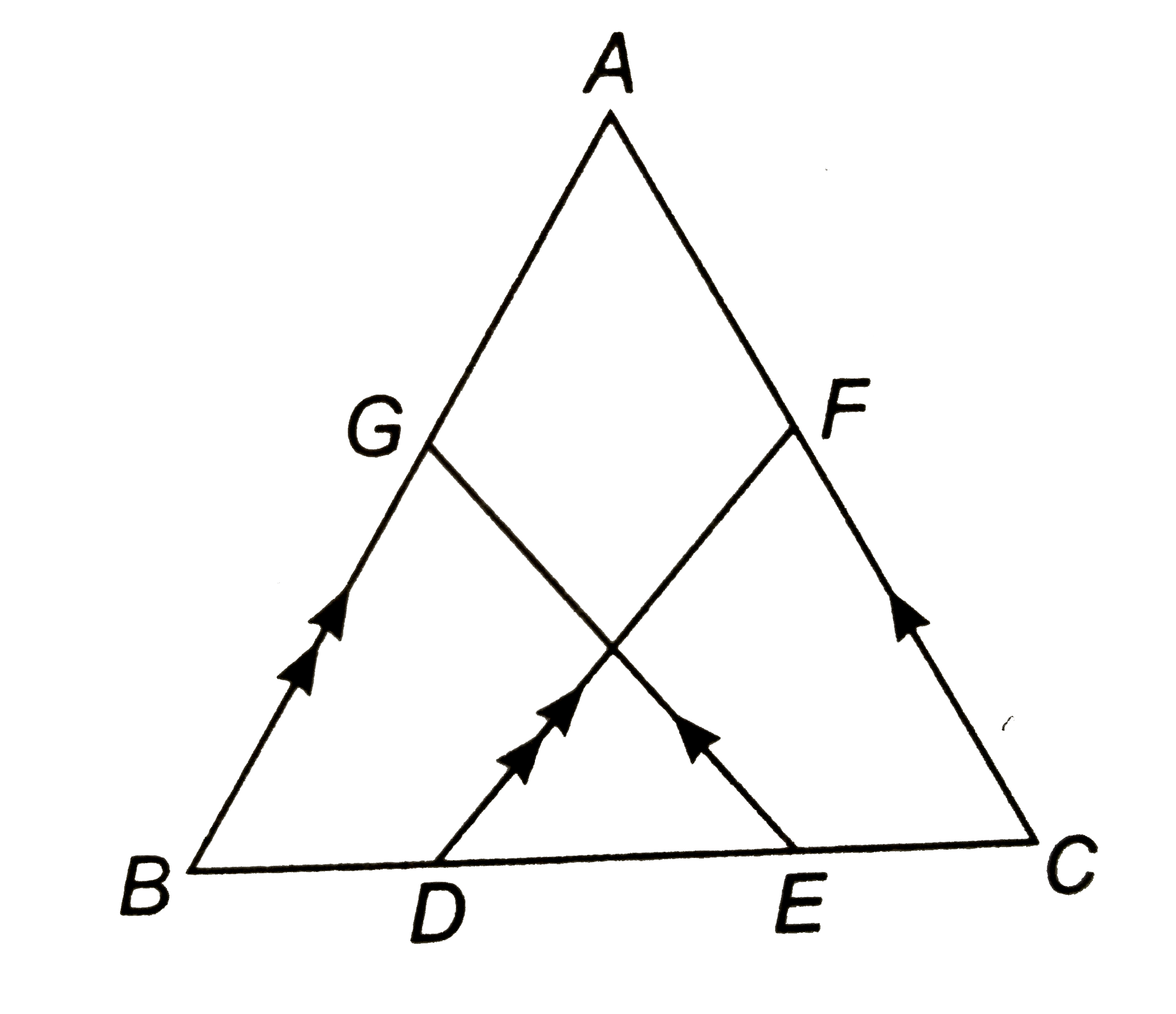
View Solutionसंलग्न आकृति में, `angleAYZ=angleBYX=90^(@),AY=YZ` और XY = BY है। सिद्ध कीजिए कि : AB=ZX

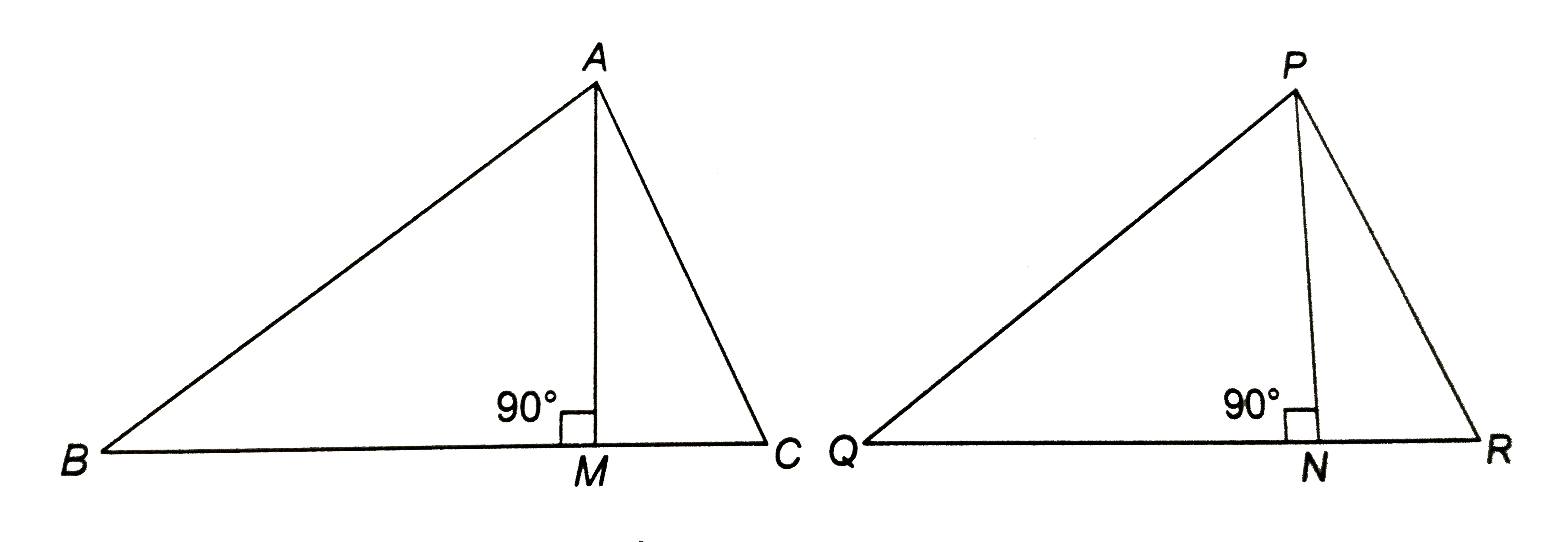
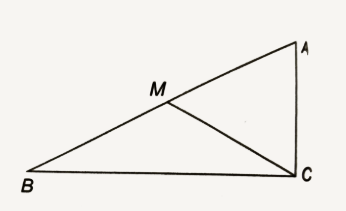
View Solutionसंलग्न चित्र में, `DeltaABC, C` पर समकोण तथा M कर्ण AB का माध्य-बिन्दु है। यदि AC=32 सेमी और BC =60 सेमी तो CM की लम्बाई ज्ञात कीजिए।
View Solution
प्रश्नावली 7A questions and complete solutions for chapter त्रिभुज of NAGEEN MATHS (HINDI) of Class 9