Complete Solutions to विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न ) of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| MADHUR GUPTA | विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न ) |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
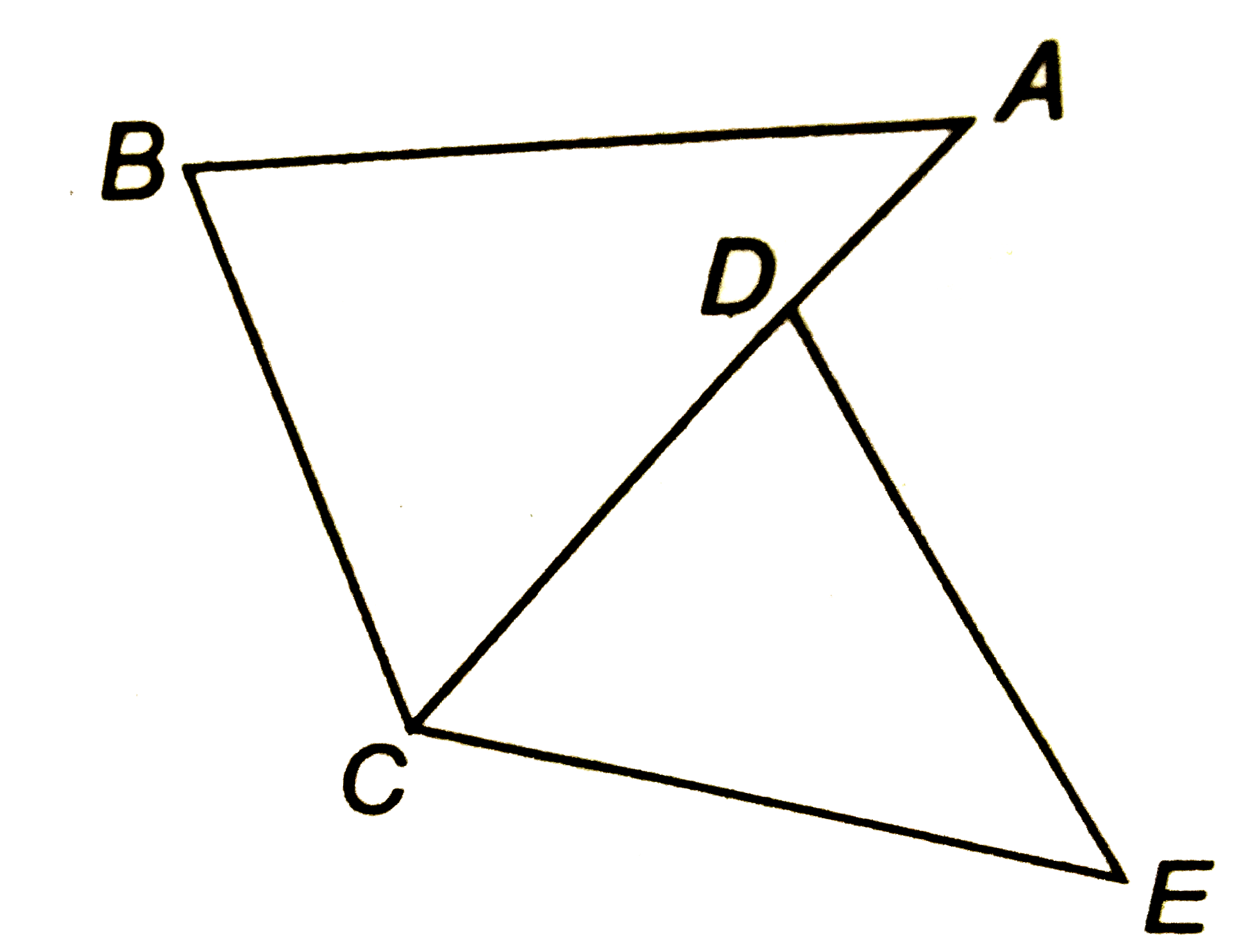
दी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
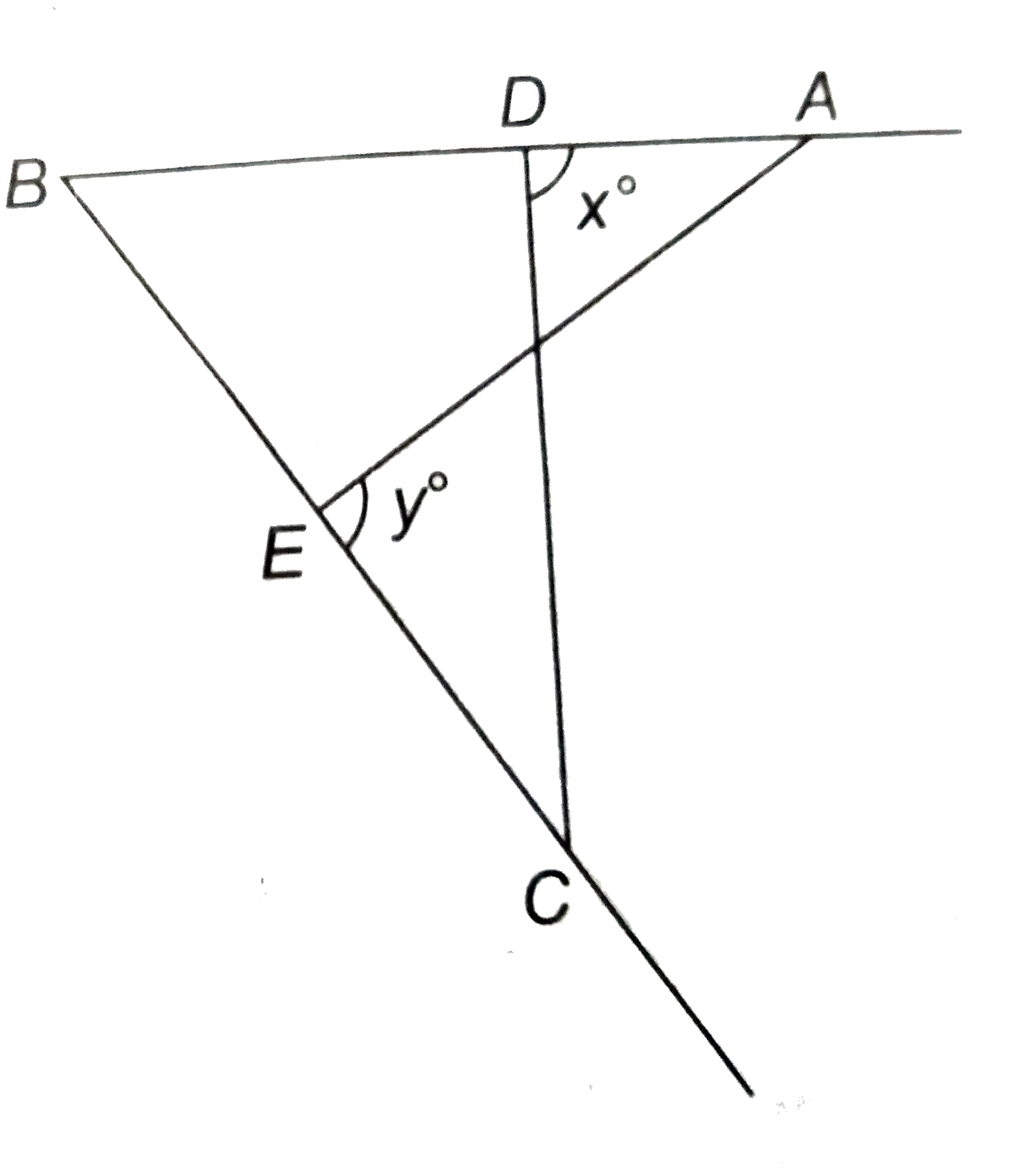
View Solution`DeltaABC" में "angleB` समकोण है। यदि BC भुजा पर BCDE एक वर्ग है और AC भुजा पर ACFG एक वर्ग है तो सिद्ध कीजिए कि AD = BF.
View Solutionदी आकृति में, ABC एक समबाहु त्रिभुज है, `PQ||AC` और AC को R तक इस प्रकार बढ़ाया गया है कि CR = BP है। सिद्ध कीजिए कि QR, PC को समद्विभाजित करती है।
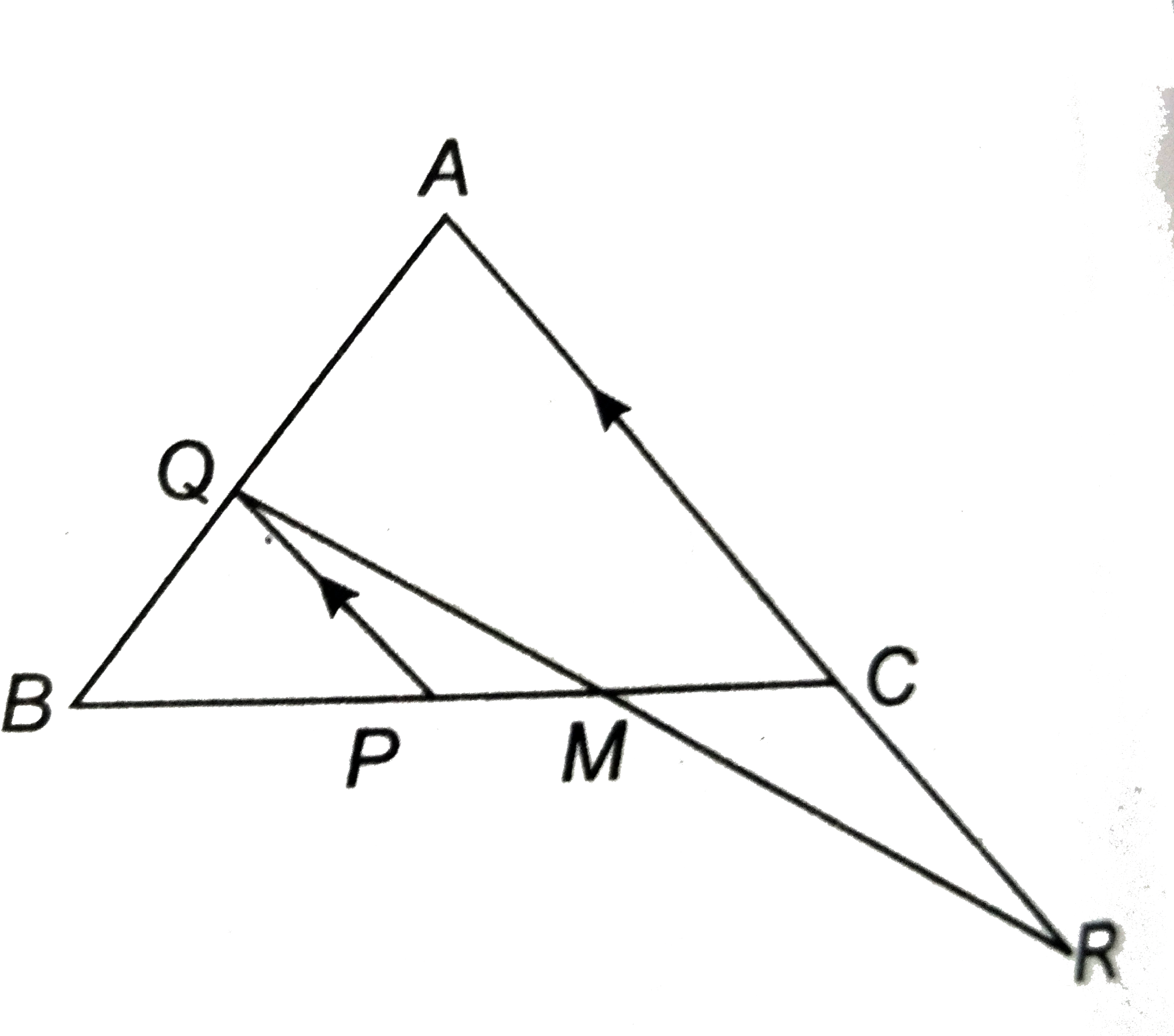
View Solutionदी आकृति में, एक चतुर्भुज ABCD दिखाया गया है। सिद्ध कीजिए कि : `AB+BC+CD+DAgtAC+BD`
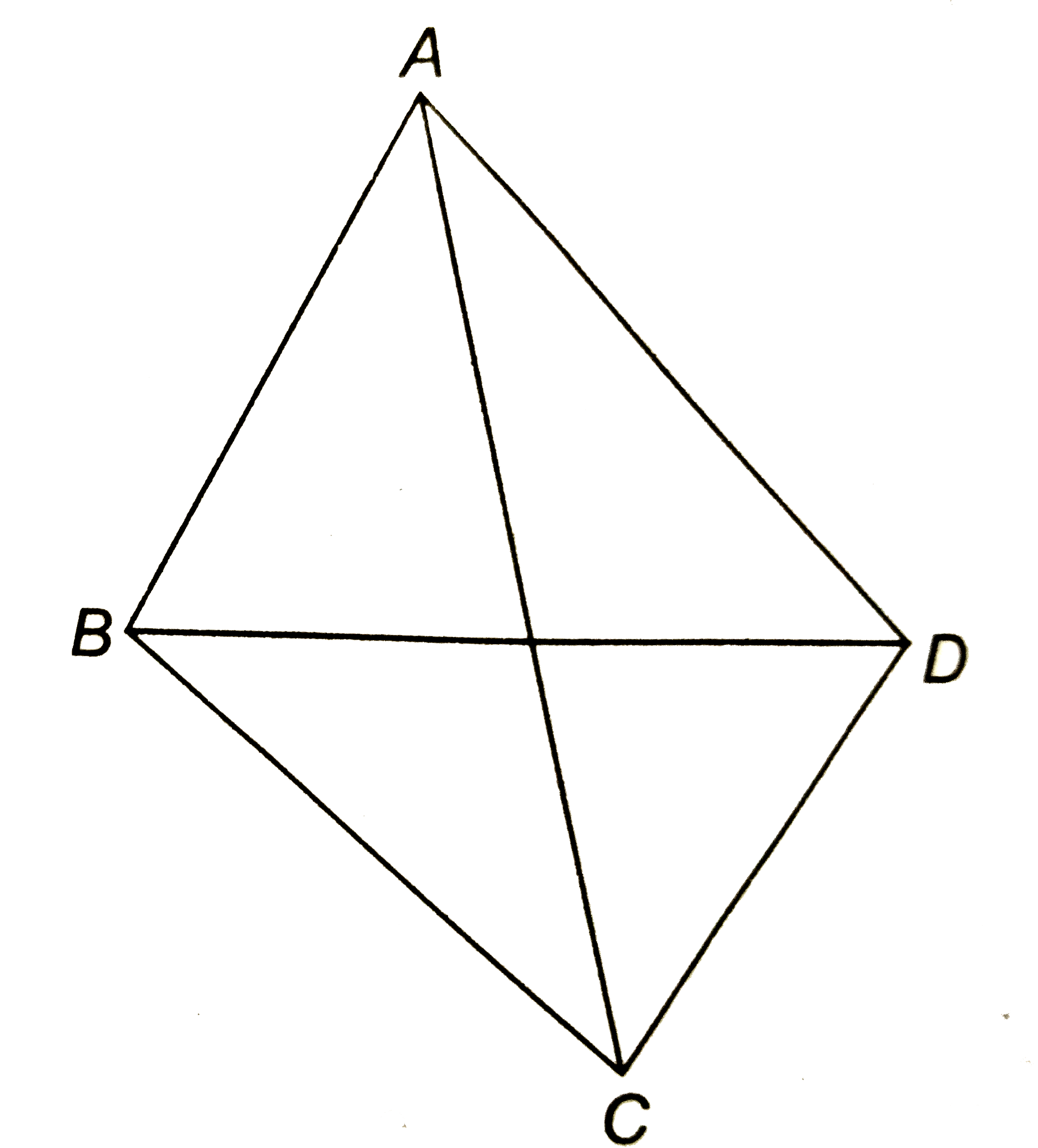
View Solutionसंलग्न चित्र में, चतुर्भुज ABCD के विकर्ण AC और BD बिन्दु O पर प्रतिच्छेद करते है। सिद्ध कीजिए कि : `AB+BC+CD+DAlt2(AC+BD)`

View Solution`DeltaABC` में, O एक आन्तरिक बिन्दु है। सिद्ध कीजिए कि : `AB+BC+CAlt2(OA+OB+OC)`
View Solutionसंलग्न चित्र में, BO और CO क्रमशः `angleCBD" और "angleBCE` के समद्विभाजक है। यदि `ACgtAB`, तो सिद्ध कीजिए कि `OBgtOC`.
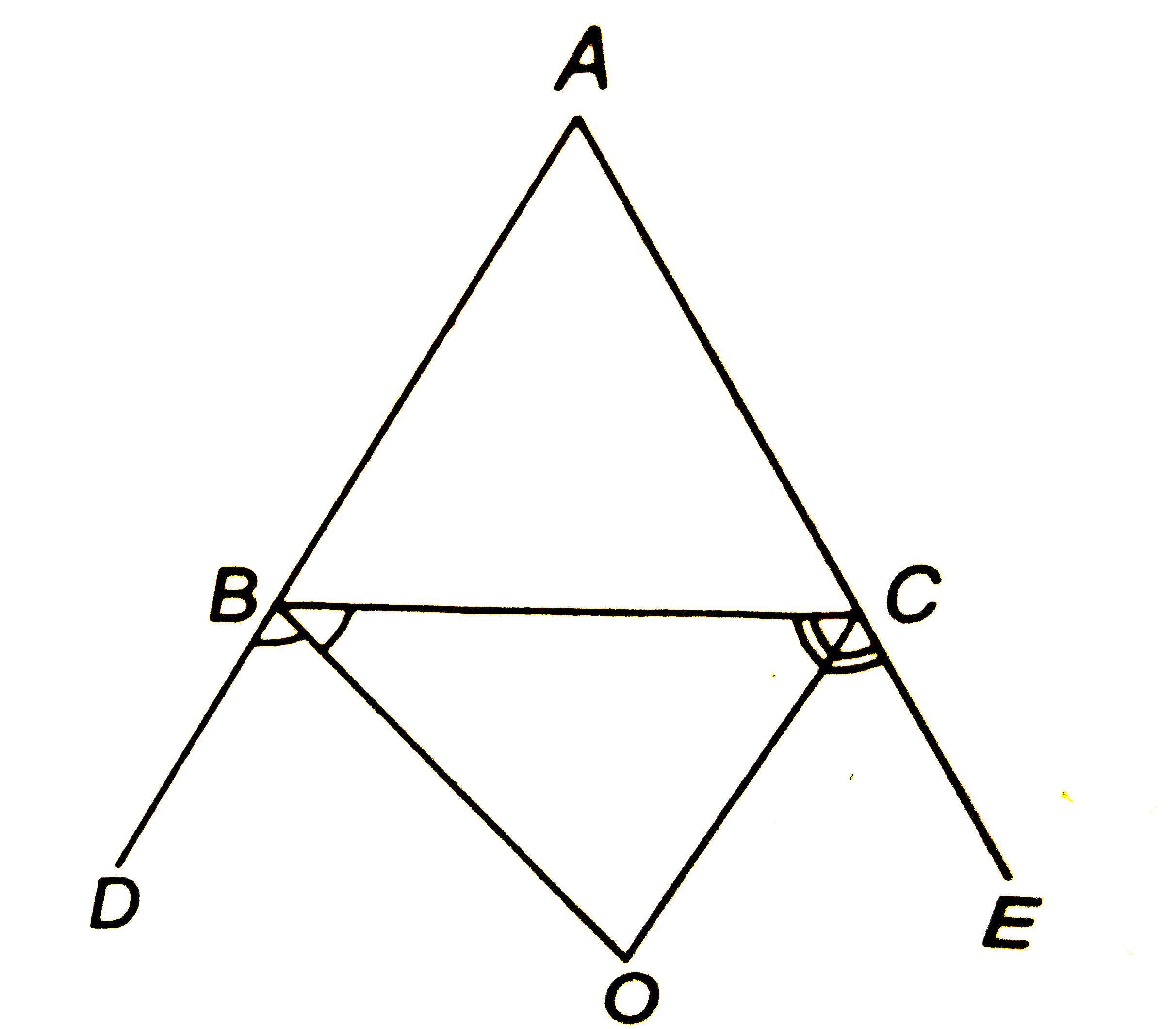
View Solutionनिम्नांकित चित्र में, यदि AD = DE है, तो सिद्ध कीजिए कि : `AB+BCgtCE`
View Solution
विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न ) questions and complete solutions for chapter त्रिभुज of NAGEEN MATHS (HINDI) of Class 9