Complete Solutions to प्रश्नावली 20.1 of chapter त्रिभुजों की सर्वांगसमता of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वांगसमता |
| S CHAND | प्रश्नावली 20.1 |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
यदि निम्नलिखित में से कोई भी सत्य है तो सिद्ध करें कि `DeltaABC` एक समद्विबाहु त्रिभुज है।
`angleBAC` का समद्विभाजक BC पर लम्ब है02:35View Solutionयदि निम्नलिखित में से कोई भी सत्य है तो सिद्ध करें कि `DeltaABC` एक समद्विबाहु त्रिभुज है।
शीर्षलम्ब AD, `angleBAC` को समद्विभाजित करता है।02:21View Solutionयदि निम्नलिखित में से कोई भी सत्य है तो सिद्ध करें कि `DeltaABC` एक समद्विबाहु त्रिभुज है।
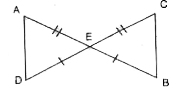
शीर्षलम्ब BE = शीर्षलम्ब CF01:51View Solutionइस आकृति में AB और CD एक दूसरे को E पर इस तरह प्रतिच्छेदित करते है कि `DE=BE` और `EA=EC` सिद्ध करें कि `AD=CB`
 02:28View Solution
02:28View Solutionआकृति में वर्ग ABCD के अन्दर X एक बिन्दु है AX के ऊपर एक वर्ग AXYZ बनाया गया है तो सिद्ध करें कि `BX=DZ`
 04:25View Solution
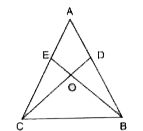
04:25View Solutionआकृति में, दिया हुआ है कि `AE=AD` और `BD=CE` तो सिद्ध करें कि `DeltaAEB ~=DeltaADC`
 03:06View Solution
03:06View Solution`DeltaABC` तथा `DeltaPQR` में, `AB=PQ,BC=QR` और CB तथा RQ को क्रमशः X तथा Y तक बढ़ाया जाता है और `angleABX=anglePQY` तो सिद्ध करें कि `DeltaABC~=DeltaPQR`
 04:25View Solution
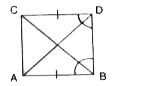
04:25View Solutionआकृति में, `AB=CD,angleABD=angleCDB` सिद्ध करें कि `AD=CB`
 02:21View Solution
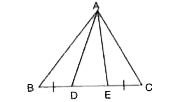
02:21View Solutionआकृति में, `DeltaABC` के आधार BC पर बिन्दु D तथा E इस प्रकार है कि `BD=CE`और `AD=AE`, तो सिद्ध करे कि `DeltaABE~=ACD`
 02:09View Solution
02:09View Solutionसिद्ध करें कि `DeltaABC` समद्विबाहु है यदि इस `DeltaABC` के माध्यिकाएँ BE और CF बराबर है
01:51View SolutionABC एक समबाहु त्रिभुज है इसकी भुजाओं BC, CA, AB पर क्रमशः D,E,F बिन्दु इस प्रकार है। कि `BD=CE=AF`, सिद्ध करें कि `DeltaDEF` एक समबाहु त्रिभुज है।
02:44View Solutionएक `DeltaABC` की भुजाओं AB और AC पर समबाहु त्रिभुज ABD तथा ACE, इस प्रकार खींची गई है कि शीर्ष D और E, `DeltaABC` के बाहर है सिद्ध करे कि `BE=DC`
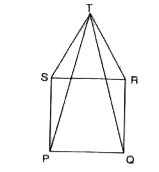
02:52View Solutionआकृति में PQRS एक वर्ग है और SRT एक समबाहु त्रिभुज है सिद्ध करें कि :
`PT=QT`
 03:15View Solution
03:15View Solutionआकृति में PQRS एक वर्ग है और SRT एक समबाहु त्रिभुज है सिद्ध करें कि :
`angleTQR=15^(@)`
 04:55View Solution
04:55View Solution
प्रश्नावली 20.1 questions and complete solutions for chapter त्रिभुजों की सर्वांगसमता of S CHAND of Class 9
All Exercises from S CHAND Class 9 MATHS त्रिभुजों की सर्वांगसमता
- प्रश्नावली 20.1
- प्रश्नावली 20.2
- प्रश्नावली 20.3
- प्रश्नावली 20.4
- प्रश्नावली 20.5
- प्रश्नावली 20.6
- प्रश्नावली 20.6 (रिक्त स्थानों को भरें)
- प्रश्नावली 20.6 (निम्नलिखित प्रकथनो में कौन- सा सत्य और कौन - सा असत्य है )
- प्रश्नावली 20.6 (रिक्त स्थानों को भरिए ताकि निम्नलिखित प्रत्येक प्रकथन सत्य हो : -)
- प्रश्नावली 20.6 (रिक्त स्थानों भरें )
- साधित उदाहरण