Complete Solutions to प्रश्नावली 20.3 of chapter त्रिभुजों की सर्वांगसमता of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वांगसमता |
| S CHAND | प्रश्नावली 20.3 |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
`DeltaABC` में A से `angleABC` के कोण समद्विभाजक BD पर खींचा गया लम्ब AD, आधार BC (जरुरी होने पर बढ़ाया हुआ) को E पर मिलता है सिद्ध करे कि `AD = DE`
View Solutionआकृति में, `PS=PR,angleTPS=angleQPR`, तो सिद्ध करे कि `AD=PQ`
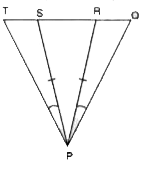
View Solutionउपर्युक्त आकृति में यदि `PQ=PT` और `angleTPS=angleQPR`, तो सिद्ध करे कि `DeltaPRS` समद्विबाहु त्रिभुज है।
View Solution`DeltaABC` के `angleA` का समद्विभाजक AD है P, AD पर कोई एक बिन्दु है सिद्ध करें कि P से AB और AC पर डाले गए लम्ब बराबर है।
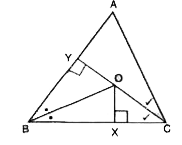
View Solutionनीचे दिए गए आकृति में, BO और CO क्रमशः त्रिभुज ABC के कोणों `angleB` और `angleC` के कोण समद्विभाजक है यदि `OX bot BC` और `OY bot AB`, तो सिद्ध करे कि
(i) `DeltaBOY ~=DeltaBOX` (ii) `OX=OY`
View Solutionसमान्तर चतुर्भुज ABCD में कोण A और C अधिककोण है बिन्दु X और Y विकर्ण BD पर इस प्रकार लिए गए है कि `angleXAD` और `angleYCB` दोनों समकोण है सिद्ध करें कि `XA=YC`
View Solution`DeltaXYZ` में, `angleY` और `angleZ` के समद्विभाजक बिन्दु O पर मिलते है बिन्दु O से क्रमशः `OP bot YZ`, `OQ bot ZX` और `OR bot XY` बनाया सिद्ध करे कि `OP=OQ=OR`
View Solution
प्रश्नावली 20.3 questions and complete solutions for chapter त्रिभुजों की सर्वांगसमता of S CHAND of Class 9
All Exercises from S CHAND Class 9 MATHS त्रिभुजों की सर्वांगसमता
- प्रश्नावली 20.1
- प्रश्नावली 20.2
- प्रश्नावली 20.3
- प्रश्नावली 20.4
- प्रश्नावली 20.5
- प्रश्नावली 20.6
- प्रश्नावली 20.6 (रिक्त स्थानों को भरें)
- प्रश्नावली 20.6 (निम्नलिखित प्रकथनो में कौन- सा सत्य और कौन - सा असत्य है )
- प्रश्नावली 20.6 (रिक्त स्थानों को भरिए ताकि निम्नलिखित प्रत्येक प्रकथन सत्य हो : -)
- प्रश्नावली 20.6 (रिक्त स्थानों भरें )
- साधित उदाहरण