Complete Solutions to प्रश्नावली 20.2 of chapter त्रिभुजों की सर्वांगसमता of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वांगसमता |
| S CHAND | प्रश्नावली 20.2 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
`DeltaABC` में, `angleA=90^(@),AB=AC` तो `angleB` और `angleC` ज्ञात करें
View Solution`DeltaABC` में, BC को D तक बढ़ाया गया है, `angleACD=110^(@)` तथा `AB=AC`, तो `angleA` ज्ञात करें।
View Solutionसिद्ध करें कि समबाहु त्रिभुज के प्रत्येक कोण का माप `60^(@)` होता है |
View Solution`anglePQR` में, `PQ=PR` बिन्दु S तथा T क्रमशः PR पर इस प्रकार है कि QT और RS क्रमशः `anglePQR` और `angleQRP` के समद्विभाजक है सिद्ध करें कि `DeltaTQR~=DeltaSRQ`
View Solutionदिए गए आकृति में `AB=AC, angleABD=angleACD` तो सिद्ध करें कि `BD=CD`
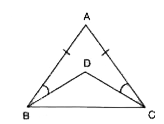
View SolutionABC एक समबाहु त्रिभुज है D में इसके अन्दर कोई बिन्दु है | DC पर एक समबाहु त्रिभुज DEC बनाया गया है जैसा कि आकृति में दिखाया गया है सिद्ध करें कि `DeltaACE` और `DeltaBCD` सर्वांगसम है।
View Solutionदिए गए आकृति में `AB=AC,angleBAD=angleCAE` सिद्ध करें कि `DeltaABE~=DeltaACD`
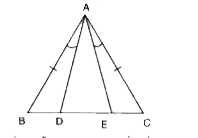
View Solutionएक समद्विबाहु त्रिभुज है जिसमें `AB=AC` और `angleB` तथा `angleC` के समद्विभाजक एक दूसरे को O पर प्रतिच्छेद करते है सिद्ध करे कि `BO=CO` और `AO," "angleBAC` का समद्विभाजक है
View Solution
प्रश्नावली 20.2 questions and complete solutions for chapter त्रिभुजों की सर्वांगसमता of S CHAND of Class 9
All Exercises from S CHAND Class 9 MATHS त्रिभुजों की सर्वांगसमता
- प्रश्नावली 20.1
- प्रश्नावली 20.2
- प्रश्नावली 20.3
- प्रश्नावली 20.4
- प्रश्नावली 20.5
- प्रश्नावली 20.6
- प्रश्नावली 20.6 (रिक्त स्थानों को भरें)
- प्रश्नावली 20.6 (निम्नलिखित प्रकथनो में कौन- सा सत्य और कौन - सा असत्य है )
- प्रश्नावली 20.6 (रिक्त स्थानों को भरिए ताकि निम्नलिखित प्रत्येक प्रकथन सत्य हो : -)
- प्रश्नावली 20.6 (रिक्त स्थानों भरें )
- साधित उदाहरण