Complete Solutions to साधित उदाहरण of chapter त्रिभुजों की सर्वांगसमता of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुजों की सर्वांगसमता |
| S CHAND | साधित उदाहरण |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
यदि शीर्षलम्ब AD, BC को समद्विभाजित करता है तो सिद्ध करें कि `DeltaABC` समद्विबाहु त्रिभुज है।
View Solutionसिद्ध करें कि `DeltaABC` एक समद्विबाहु त्रिभुज है यदि माध्यिका AD, BC पर लम्ब है।
View Solutionआकृति में, AB तथा CD का मध्य बिंदु ० है सिद्ध करें कि AC = BD तथा `AC||BD`.

View Solutionआकृति में, दिया हुआ है कि `AB=CF,EF=BD` और `angleAFE=angleDBC`. सिद्ध करे कि `DeltaAFE~= DeltaCBD`
View Solutionआकृति में X तथा Y, `DeltaABC` की समान भुजाओं AB और AC पर दो बिन्दु इस प्रकार है कि `AX=AY` तो सिद्ध करे कि `XC=YB`
View Solutionआकृति में, `PS=QR` और `angleSPQ=angleRQP` तो सिद्ध करें कि `PR=QS` और `angleQPR=anglePQS`
View Solutionआकृति में, चतुर्भुज ABCD की सम्मुख भुजाओं AB और DC की मध्य - बिंदुओं M और N को जोड़ने वाला रेखाखण्ड दोनों भुजाओं पर लम्ब है सिद्ध करें कि चतुर्भुज की अन्य भुजाएँ बराबर है।
View Solutionआकृति में, `AC = AE` तथा `AB=AD` और `angleBAD=angleEAC`. सिद्ध करें कि `BC=DE`.
View Solutionएक समकोण त्रिभुज ABC के कर्ण AC का मध्य बिन्दु D है तो सिद्ध करें कि `BD=1/2AC`
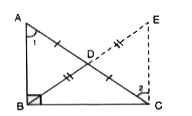
View Solutionहमीदा दो वस्तुओं A और B के बीच की दूरी ज्ञात करना चाहती है परन्तु इन दोनों वस्तुओं के बीच एक रूकावट है जिसके कारण वह यह दूरी सीधे नाप कर ज्ञात नहीं कर सकती है इस कठिनाई को दूर करने के लिए वह एक चातुर्य विधि का प्रयोग करती है पहले वह एक सुविधाजनक बिन्दु O ऐसा लेती है जहाँ से A और B दोनों दिखाई दें और वहां एक खंभा स्थापित करती है तब रेखा OA की सीध में एक बिन्दु D पर वह दूसरा प्रकार स्थापित करती है वह कि OA = DO। इसी प्रकार वह तीसरा खंभा रेखा BO की सीध में बिन्दु C पर स्थापित करते है जिससे कि BO = CO।
तब वह CD को नापती है और देखती है कि CD = 540 सेमी सिद्ध कीजिए कि A और B के बीच की दूरी भी 540 सेमी है।

View Solution`DeltaABC` में `angleA=120^(@)` और `AB=AC, angleB` और `angleC` ज्ञात करें।
View Solutionआकृति में, `AB=AC` और `angleACD=140^(@)` तो `angleA` ज्ञात करें।
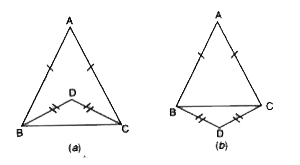
View Solution`DeltaABC` एक समद्विबाहु त्रिभुज है जिसमे `AB=AC` | D, E और F क्रमशः भुजाएँ BC, AC और AB के मध्य - बिन्दु है सिद्ध करे कि `DE=DF`
View Solutionसिद्ध करे कि समद्विबाहु त्रिभुज के बराबर भुजाओं को समद्विभाजित करने वाली माध्यिकाएँ भी बराबर होते है।
View Solutionआकृति में `AB=AC` और `DB=DC` सिद्ध करें कि `angleABD=angleACD`.
View Solution`DeltaABC` में `AB=AC` और `angleB` तथा `angleC` के समद्विभाजक बिन्दु O पर प्रतिच्छेद करते है सिद्ध करें कि `BO=CO` और किरण AO कोण BAC का समद्विभाजक है।
View Solutionआकृति में दिया है : `AB=BC` और `AD=EC`, तो सिद्ध करे कि `DeltaABE~=DeltaCBD`
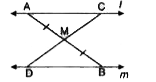
View Solutionदी गई आकृति में `l||m` और M, रेखाखण्ड का मध्य - बिन्दु है सिद्ध करे कि M, रेखाखण्ड CD का भी मध्य - बिन्दु है जिसके अंत बिन्दु क्रमशः l और m पर है।
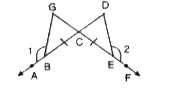
View Solutionदी गई आकृति में दिया है कि `BC=CE` और `angle1=angle2` तो सिद्ध कीजिए कि `DeltaGCB~=DeltaDCE`
View Solutionदिए गए आकृति में चतुर्भुज ABCD का विकर्ण AC कोण A और C को समद्विभाजित करता है सिद्ध करें कि `AB=AD` और `CB=CD`
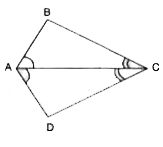
View Solutionदिए गए आकृति में यह है कि `AB=EF,BC=DE,AB bot CE` तो सिद्ध करे कि `DeltaABD~= DeltaFEC`

View Solutionदिए गए आकृति में, AP और BQ रेखाखण्ड AB पर लम्ब है और `AP=BQ` तो सिद्ध करें कि बिन्दु O रेखाखण्ड AB और PQ का मध्य - बिन्दु है।
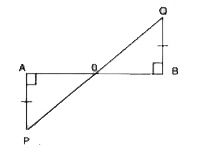
View Solutionनीचे दी गई आकृति में यह व्याख्या कीजिए कि नदी को पार किए बिना कोई उसकी चौड़ाई कैसे ज्ञात कर सकता है।

View Solutionदिए गए आकृत में AB का मध्य - बिन्दु C है |
`angleBAD=angleCBE` और `angleECA=angleDCB`
सिद्ध करे कि (i) `DeltaDAC~=DeltaEBC` (ii) `DA=EB`

View Solutionदिए गए आकृति में `angleCPD=angleBPD` और AD, `angleBAC` समद्विभाजक है तो सिद्ध करें कि
`DeltaCAP~=BAP` और `CP=BP`.
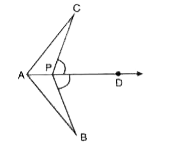
View Solutionआकृति में AD एक माध्यिका है और BL, CM क्रमशः B तथा C से AD और AD के बढ़े हुए भाग पर खींचे गए लम्ब है तो सिद्ध करे कि `BL=CM`

View Solutionआकृति में BM और DN ही रेखाखण्ड AC पर लम्ब है और `BM=DN` सिद्ध कीजिए कि AC, BD को समद्विभाजित करता है।
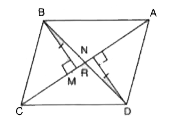
View Solutionदिए गए आकृति में, `AB||DC` और P, BD का मध्य - बिन्दु है साबित करे कि P, AC का भी मध्य - बिन्दु है।
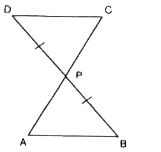
View SolutionAB एक रेखाखण्ड है रेखाखण्ड AB के सम्मुख दो बराबर रेखाखण्ड AX और BY इस प्रकार खींचे गए है कि `AX||BY` यदि AB बिन्दु P पर एक दुसरे को प्रतिच्छेद करते है तो सिद्ध करें कि : -
(i) `DeltaAPX~=DeltaBPY` (ii) AB और XY एक दूसरे को समद्विभाजित करते है
View Solutionएक समद्विबाहु त्रिभुज ABC, जिसमेंAC = BC तथा BE क्रमशः इसके शीर्षलम्ब है तो सिद्ध करे कि `AE=BD`
View Solutionआकृति में PQRS एक चतुर्भुज है तो T तथा U क्रमशः PS और RS पर ऐसे बिन्दु है कि `PQ=RQ," "anglePQT=angleRQU` और `angleTQS=angleUQS` तो सिद्ध करे कि `QT=QU`

View Solutionत्रिभुज एक समद्विबाहु त्रिभुज है जिसमें `AB=AC` | भुजा BA को D तक इस प्रकार बढ़ाया कि सिद्ध करें कि `angleBCD` एक समकोण है।
View Solutionयदि एक समद्विबाहु त्रिभुज ABC में AB=AC दिया हो, तो सिध्द करो कि शीर्ष B तथा C से उनकी सम्मुख भुजाओं पर डाले गए लम्ब बराबर होंगे हैं |
View Solutionयदि एक त्रिभुज की दो शीर्षो से सम्मुख पर खींचे गए शीर्षलम्ब बराबर हो तो सिद्ध करें कि त्रिभुज समद्विबाहु है।
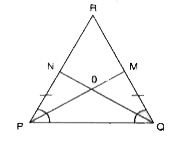
View Solutionआकृति में, `angleQPR=anglePQR` और `DeltaPQR` की भुजाओं QR और PR पर क्रमशः M और N ऐसे बिन्दु है कि `QM=PN` | सिद्ध कीजिए कि `OP=OQ` जहाँ PM तथा QN का प्रतिच्छेदन बिन्दु O है।
View Solutionआकृति में `AB=AC`. और `angleB` तथा `angleC` के समद्विभाजक क्रमशः BE तथा CF है तो सिद्ध करे कि `DeltaEBC ~=DeltaFCB`.
View Solutionआकृति में दिया हुआ है : `angleA=angleC` तथा `AB=BC` तो सिद्ध करें कि `DeltaABD~=CBE`
View Solutionएक समकोण त्रिभुज में एक न्यूनकोण दूसरे कोण का दुगुना है तो सिद्ध कीजिए कि कर्ण छोटी भुजा का दुगुना है।
View Solutionआकृति में दिया है कि `AB=CD` और `AD=BC` सिद्ध करें `DeltaADC~=DeltaCBA`.
View Solutionआकृति में `AD=BC` तथा `BD=CA` सिद्ध करें कि `angleADB=angleBCA` तथा `angleDAB=angleCBA`
View SolutionABCD एक समान्तर चतुर्भुज है यदि इसके विकर्ण बराबर है तो `angleABC` का माप ज्ञात कीजिए।
View Solutionआकृति में, त्रिभुज ABC की दो भुजाएँ AB तथा BC और माध्यिका AD क्रमशः दूसरा त्रिभुज PQR की दो भुजा PQ तथा QR और मध्यिका PM के बराबर है सिद्ध कीजिए कि `DeltaABC~=DeltaPQR`.
View Solutionयदि दो समद्विबाहु त्रिभुज का एक ही आधार हो, तो सिद्ध कीजिए कि उनके शीर्षो को मिलाने वाली रेखा आधार को समकोण बनाती हुई समद्विभाजित करती है।
View Solutionचार समान भुजाओं वालो एक आकृति ABCD में बिन्दु O इस प्रकार है कि इसकी दूरियां बिन्दु D और B से बराबर है दर्शाइए कि OA , OC एकरेखीय है।
View Solutionयदि एक समद्विबाहु `DeltaABC` इस प्रकार है कि `AB=AC` तो सिद्ध करें कि शीर्षलम्ब AD (A से खींचा हुआ भुजा BC पर) BC को समद्विभाजित करता है।
View Solution`DeltaABC` के शीर्ष लम्ब AD और इस प्रकार है कि `AE=BD` | सिद्ध करे कि `AD=BE`
View Solutionआकृति में `LM=MN,QM=MR bot PQ` तथा `MN bot PR`, तो सिद्ध करे कि `PQ=PR`.
View Solutionएक `DeltaABC` के शीर्षलम्ब AD, BE तथा CF बराबर है सिद्ध करे कि `DeltaABC` समबाहु त्रिभुज है।
View Solutionएक प्रेक्षण D पर बैठा और एक दर्पण LM के सामने बिन्दु A पर रखी हुई वस्तु का प्रतिलम्ब बिन्दु B पर दिखाई देता है सिद्ध करें कि जितनी दूरी दर्पण से वस्तु की AT है उतनी ही दर्पण से प्रतिबिम्ब की BT है।
View Solution
साधित उदाहरण questions and complete solutions for chapter त्रिभुजों की सर्वांगसमता of S CHAND of Class 9
All Exercises from S CHAND Class 9 MATHS त्रिभुजों की सर्वांगसमता
- प्रश्नावली 20.1
- प्रश्नावली 20.2
- प्रश्नावली 20.3
- प्रश्नावली 20.4
- प्रश्नावली 20.5
- प्रश्नावली 20.6
- प्रश्नावली 20.6 (रिक्त स्थानों को भरें)
- प्रश्नावली 20.6 (निम्नलिखित प्रकथनो में कौन- सा सत्य और कौन - सा असत्य है )
- प्रश्नावली 20.6 (रिक्त स्थानों को भरिए ताकि निम्नलिखित प्रत्येक प्रकथन सत्य हो : -)
- प्रश्नावली 20.6 (रिक्त स्थानों भरें )
- साधित उदाहरण