ΔABC సమద్విబహు త్రిభుజంలో AB=AC,AD ఒక ఉన్నతి, ∠BAD=50∘ అయిన ∠CAD=
40∘
130∘
50∘
ఏదికాదు
Step by step video & image solution for Delta ABC సమద్విబహు త్రిభుజంలో AB=AC,AD ఒక ఉన్నతి, /_BAD =50^@ అయిన /_CAD= by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- త్రిభుజాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - త్రిభుజాలుEXERCISE - Exercise
89 Videos
- జ్యామితీయ మూలాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - జ్యామితీయ మూలాలుEXERCISE - Exercise
47 Videos
- నిరూపక జ్యామితిBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - నిరూపక జ్యామితిEXERCISE - Exercise
87 Videos
Similar Questions
చతుర్భుజం ABCD లో , AC=AD మరియి ∠A కు AB కోన సమద్విఖండన రేఖ అయిన ΔABC=ΔABD అని చూపండి. BC మరియు BD ల గురించి మీరు ఏమి చెప్పగలరు?
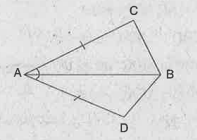
View Solutionకింది వానికి జవాబులు ఇవ్వండి. ఘనాలకు ఎన్ని కొలతలు ఉంటాయి?
View Solutionఒక ఆవాస ప్రాంతంలో ప్రధాన రహదారి ఉత్తర-దక్షిణ దిశలలో ఉంది. దాని పటం కింది ఇవ్వబడినది. పటం సహాయంతో కింది ప్రశ్నలకు సమాధానాలు వ్రాయండి.
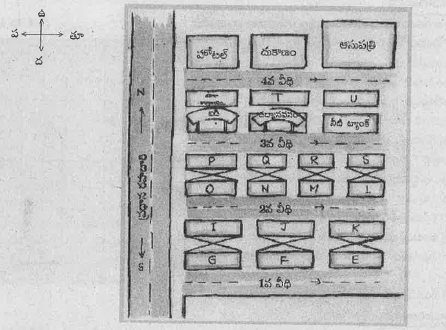 తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?
తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?
View SolutionIn Delta ABC, if AB=AC and /_A=50^(@), then /_C=
View SolutionIn Delta ABC, if AB=AC and /_A=50^(@), then /_C=
View SolutionIn Fig. 4.58, ABC is a triangle such that ABAC=BDDC, ∠B=70o, ∠C=50o . Find ∠BAD . (FIGURE)
View SolutionIn fig.39, AD and CF are respectively perpendiculars to sides BC and AB of ABC. if ∠FCD=500, f∈d ∠BAD.
View SolutionIn the adjoining figure, AB=AC and BD=DC Prove that Delta ADB-=Delta ADC and hence show that (i) /_ADB-=/_ADC=90^(@) , (ii) /_BAD=/_CAD
View SolutionΔABC में AD भुजा BC का लम्ब समद्विभाजक है। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
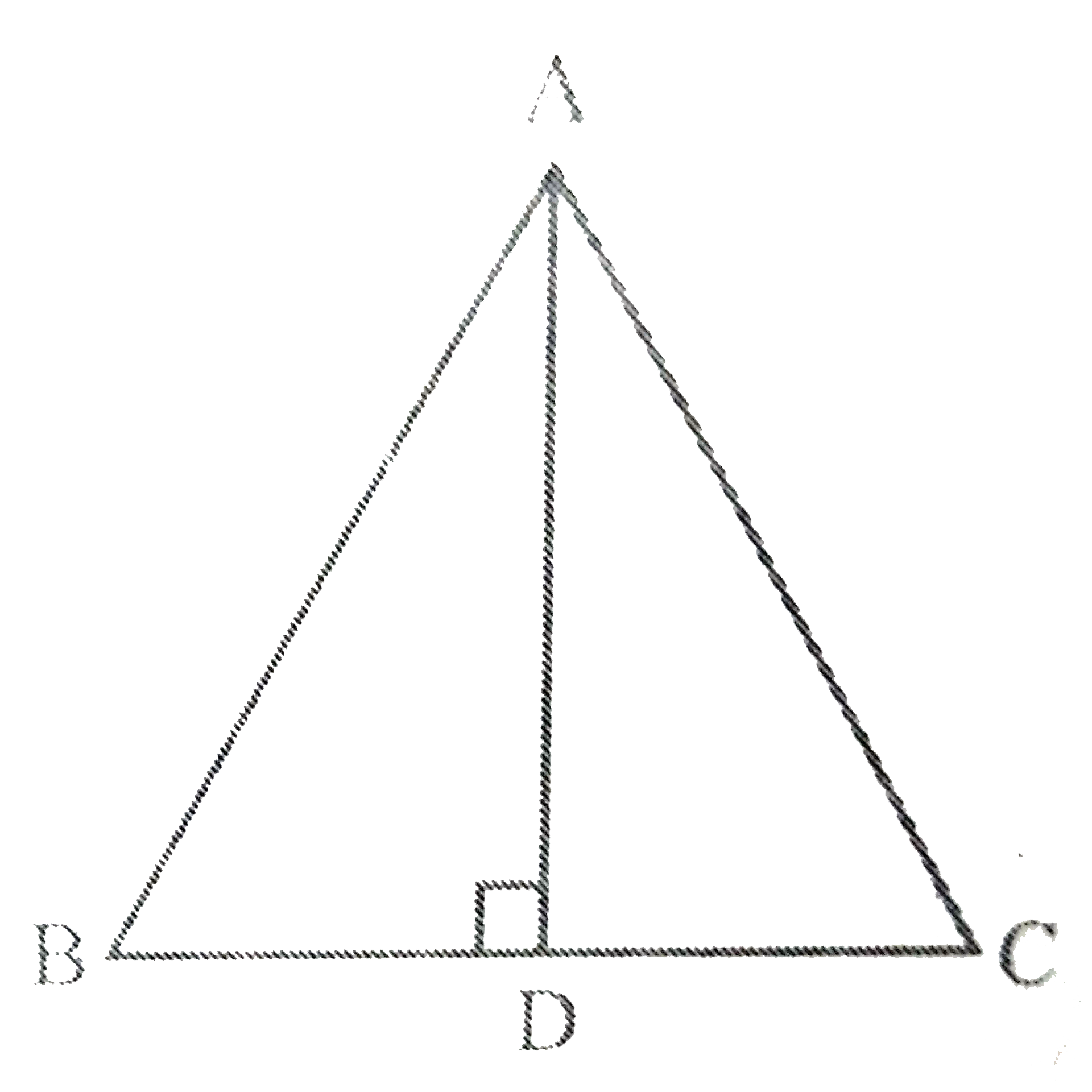
View Solutionचित्र में AB=3 सेमी AC=6 सेमी BD=2 सेमी और CD=4 सेमी तो ∠BAD और ∠CAD का अनुपात होगा-
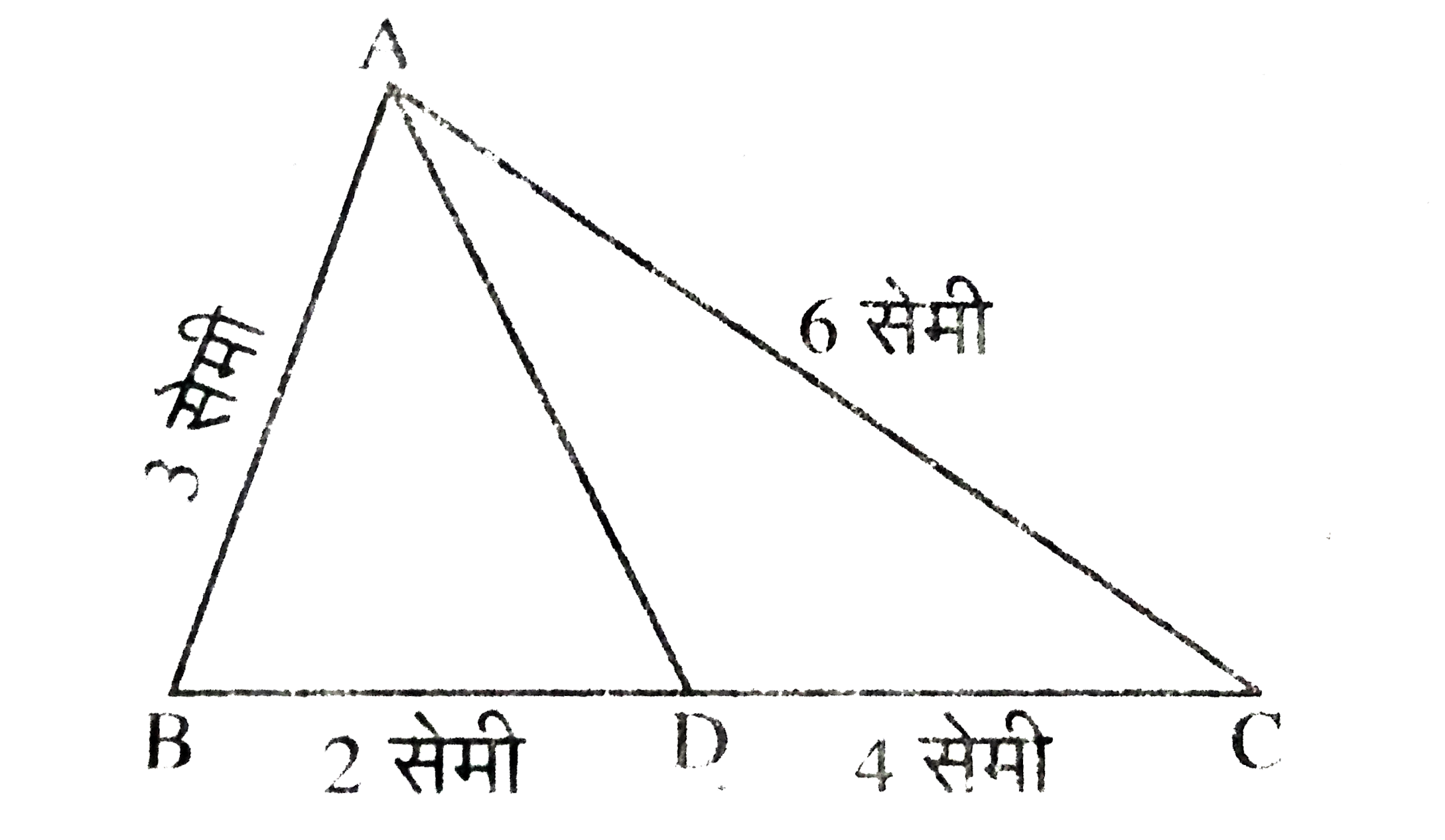
View SolutionIn △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
View SolutionIn an isosceles right angled , triangle ABC,∠B=900,AD is the median,then sin∠BADsin∠CAD is:
View SolutionIn an isosceles right angled triangle ABC, ∠B=900, AD is the median, then sin∠BADsin∠CAD is
View SolutionDelta ABC In /_BAD = /_CAD And BD = DC, which
View SolutionΔABC,AB=AC and BA is produced to D such that AC = AD. Then the ∠BCD is
View Solution
