Solved Examples from NAGEEN PRAKASHAN ENGLISH VOLUME AND SURFACE AREA OF SOLIDS for Class 10
| Class 10 | MATHS |
| Chapter | VOLUME AND SURFACE AREA OF SOLIDS |
| NAGEEN PRAKASHAN ENGLISH | Solved Examples |
| Medium | English |
| Academic Year | 2023-2024 |
Question 21
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other end. Given that common radius =3.5 cm the height of the cylinder =6.5 cm and the total height =12.8 cm , claculate the volume of the solid correct to the nearest cm.
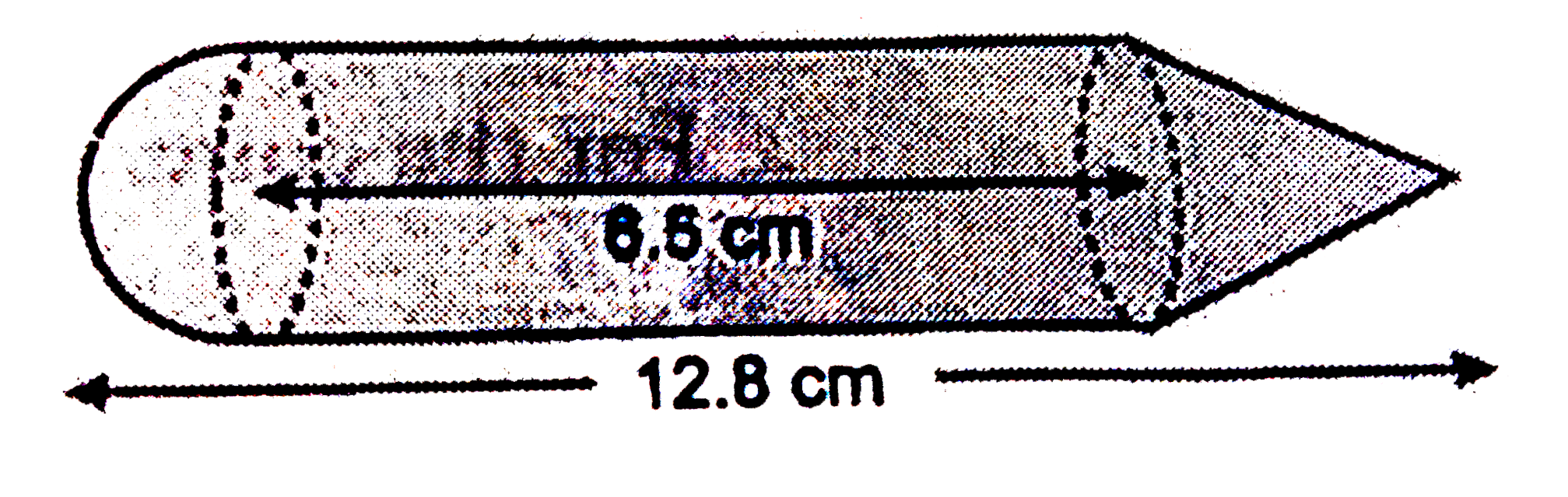 View Solution
View SolutionQuestion 25
A solid metal sphere is melted and smaller sperees of equal radii are formed. 10% of the volume of the sphere is lost in the process. The smaller spheres have a radius , that is 19 th the larger sphere . Iof 10 litres of paint were needed to paint the larger sphere. Find how many letres are needed to paint all the smaller spheres? View SolutionQuestion 35
A rectangualr container whose base is a square of side 15 cm stands on a horizointal table and holds water up to 3cm from the top .When a cube is placed in the water and is completely submerged , the water rises to the top and 54 cm3 of water overflows.
Calculate the volume of the cube and its surface area. View SolutionQuestion 66
Shubham pal an engineering student was asked to make a model shaped like cylinder wih two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm .If each cone has a height of 32 cm , find the volufme of air contained in the model that shubham pal made. (Assume the outer and inner dimensions of the model to be nearly the same).View SolutionQuestion 69
A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measuremets.View SolutionQuestion 71
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required. (Use π=22/7 )View Solution