Exercise (B) from BHARATI BHAWAN PHYSICS (HINGLISH) LAWS OF MOTION, FREE BODY DIAGRAM for Class 11
| Class 11 | PHYSICS |
| Chapter | LAWS OF MOTION, FREE BODY DIAGRAM |
| BHARATI BHAWAN PHYSICS (HINGLISH) | Exercise (B) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
The metal blocks A and B of masses 2 kg and 1 kg , respectively are in contact on a frictionless table A constant horizontal force of 3 N is applied to the block A . Calculate the force of constant between the two blocks . If the same force is applied to the block B then what will be the force of contact ? Can you explain the difference ? View SolutionQuestion 3
Three metal blocks A , B and C of masses 10 kg , 20 kg and 30 kg rest on a frictionless table in a line . A is converted to B and B to C by two pieces of string . With the help of a third string attached to C , the system is pulled to the right with a force of 60 N . Find the tensions of the first and second strings . View SolutionQuestion 6
A uniform rope of length L , resting on frictionless horizontal table is pulled at one end by a force F . What is the tension in the rope at a distance x from the end where the force is applied ?
[ Hint : Consider the motion of the entire rope and the motion of x length of rope using P = ma formula and third law of motion ] View SolutionQuestion 8
A block of mass 3kg which is on a smooth inclined plane making angie of 30∘ to the horizontal is connected by cord passing over light frictionless pulley to second block of mass 2kg hanging vertically. What is the acceleration of each block and waht is the tension of the cord ? .View SolutionQuestion 11
A block slides down a frictionless incline kept on the floor of a chamber . Find the acceleration of the block relative to the incline when the chamber is carried by a helicopter with upward acceleration a at inclination θ with the vertical . Consider the special cases when θ=0∘ and θ=90∘ . The inclination of the plane is 90∘−α to the vertical in the same sense as θ . View SolutionQuestion 13
A box is put on the platform of a spring balance which is adjusted to zero when the box is empty . A stream of pebbles is then poured into the box from height h above its bottom at a constant rate of n pebbles per second . Find the scale reading t seconds after the pebbles begin to fill the box , assuming that the collisions between the pebbles and the box are completely inelastic . View SolutionQuestion 14
A scale is adjusted to zero . Particles fall from a height h = 250 m before colliding with the balance pan of the scale . The collisions are elastic . If each particle has a mass of m = 100 mg and collisions occur at the rate n = 1000 particles per second , what is the scale reading in kg ? View SolutionQuestion 15
An electron of mass m is involved in head-on collision with an atom of mass M , initially at rest . As a result of the collision a certain amount of energy E is stored internally in the atom . What is the minimum initial velocity that the electron must have ?
[Hint : Since energy is stored in the atom , the collision is essentially inelastic . mv = mv' + Mv'' and 12mv2=E+12mv2+12Mv''2 . Solve for v' and apply the condition for real values of v'.)View SolutionQuestion 16
Two bodies 1 and 2 of masses m and M are kept slightly separated . A third body 3 of mass m coming from left with velocity v makes a head- on elastic collision with m . Show that if m≥M there are exactly two collisions and find all final velocities and if m≤M there are three collisions and find all final velocities . View SolutionQuestion 17
A steel ball weighting 1 kg is fastened to a cord 1 m long and is released when the cord is horizontal . At the bottom of its path the ball strikes a 5-kg steel block initially at rest on a frictionless surface . The collision is elastic . Find the speed of the ball and speed of the block just after collision . (g = 9.8ms−2)
[Hint : Apply principal of conservation of momentum and conservation of kinetic energy as the collision is elastic .]View SolutionQuestion 18
An elevator (a lift ) is moving up at the speed of 2 m/s in a shaft . At the instant the elevator is 20 m from the top , a ball is dropped from the top of the shaft . The ball rebounds elastically from the elevators roof . To what height can it rise relative to the top of the shaft ? View SolutionQuestion 19
An elevator is provided with a weighing machine ( making use of principle of spring balance ) at its floor . A man weighing 60 kg stands on the platform of the machine and finds that the reading shoots to 62 kg when the elevator starts and then comes down to 60 kg again. How do you explain this ? View SolutionQuestion 20
A projectile of mass 50 kg is projected vertically upwards with a velocity of 100 m/s . After 5 seconds it explodes into two pieces , one piece of 20 kg moving vertically upward with velocity 150 m/s . Calculate the velocity of the other piece and also the algebraic sum of the momenta of the system 3 s later . View SolutionQuestion 22
A cord is tied at one end to a sprind balance of weight 3 kg supporting a mass of 5 kg . The cord passes over a smooth fixed pulley carrying a load of 10 kg at the other end . What will be the reading of the spring balance when the system moves ? How will the reading vary if the load of 10 kg be replaced by a load of 6 kg ?
[Hint : Consider free-body diagrams of 5 kg , 10 kg and the system (5 kg body + 3 kg spring ).]View SolutionQuestion 24
A plumb bob hanging from the ceiling of railroad car acts as an accelerometer . Derive the general expression relating the horizontal acceleration a of the car with the angle θ made by the bob with the vertical . Find θ when a=1.5ms−2 and a when θ=10∘
[Hint: Apply d' Alembert's principal.] View SolutionQuestion 27
A machine gun is mounted on a flat railroad car . The gun is firing bullets at the rate of 10 bullets per second each of mass 10 g . The bullets come out with velocity 500ms−1 relative to the car . Calculate the acceleration of the car at the instant when its mass is 200 kg . Also calculate the force at that instant.View SolutionQuestion 28
A train of mass M is travelling with a uniform velocity on a level line . The last carriage whose mass is m gets detached from the train . The driver of the train discovers it only after travelling a distance l and then he shuts off steam . Show that when both parts come to rest the distance between them is (MlM−m) . Assume resistance of motion to be uniform and proportional to mass and the pull of the engine to be a constant . View SolutionQuestion 29
A cannon and a supply of cannon balls are inside a sealed rail road car. The cannon fires to the right, the car recoils to the left. The canon balls remain in the car after hitting the far wall. Show that no matter how the cannon balls are fired, the rail road car cannot travel more than L. assuming it starts from rest.
 View Solution
View SolutionQuestion 30
A jet airplane is travelling at 200ms−1 . The engine of the plane takes in 250 m3 of air of mass 32 kg each second . The air is used to burn 3 kg of fuel each second . The energy is used to compress the products of combustion to eject them at the rear of the plane at 500ms−1 relative to the plane . Find the power of the jet plane in H.P.(1 H.P = 746 W).
[Hint : Resultant thrust = forward thrust - backward thrust and power = force × velocity ]View SolutionQuestion 31
Sand drops from a stationary hopper at the rate of 5 kg s−1 on to a conveyor belt moving with a constant speed of 2ms−1 . What is the force required to keep the belt moving and what is the power delivered by the motor moving the belt ?
[ Hint: Tangetial force exerted on the belt = ureldMdt where urel is the tangential relative velocity of the sand .]View SolutionQuestion 32
A right-angled triangular block of mass M rests on a horizontal table . The inclination of the block is 30∘ with the table . A cubical block of mass m is placed on the incline of the block . What horizontal force must be applied on M so that m may remain stationery relative to the block ?
[Hint: Apply d' Alember's principal and consider free-body diagrams of m and the system ( m+ M).]View SolutionQuestion 34
A wedge of mass M rests with one face in contact with horizontal , smooth surface . A particle of mass m is placed on the smooth face on it , inclined at an angle αto the horizontal and released . Find the velocity of the wedge and that of the particle relative to the wedge when the particle has slipped a distance x down the face of the wedge . Also calculate the acceleration of the wedge and that of the particle relative to the wedge and the smooth surface .
[Hint : Apply principal of conservation of momentum along the horizontal and energy conservation principle . See Example 8 )View SolutionQuestion 35
Two identical buggies 1 and 2 with one man in each move without friction due to inertia along the parallel rails toward each other. When the buggies get opposite each other, the men exchange their places by jumping in the direction perpendicular to the motion direction. As a consequence, buggy 1 stops and buggy 2 keeps moving in the same direction, with its velocity becoming equal to v. Find the initial velocities of the buggies v1 and v2 if the mass of each buggy (without a man) equals M and the mass of each man m.View SolutionQuestion 36
Two identical buggies move one after the other due to inertia (without friction) with the same velocity v0. A man of mass m rides the rear buggy. At a certain moment the man jumps into the front buggy with a velocity u relative to his buggy. Knowing that the mass of each buggy is equal to M, find the velocities with which the buggies will move after that. View SolutionQuestion 37
Assuming that the car in problem 12 is initially at rest and holds n men, each of mass m, prove that if the men run with relative velocity vrel and jump in succession they can impart to the car a greater velocity than if they all run and jump simultaneously.
[Hint : When the men run together, the effect is the same as for one man of mass nm.
∴Δv=nmM+nmvrel.
When they run and jump in succession,
Δv=i=n∑i=1=mvrelM+im=mvrel(1M+m+1M+2m+1M+3m+...+1M+nm)] View SolutionQuestion 38
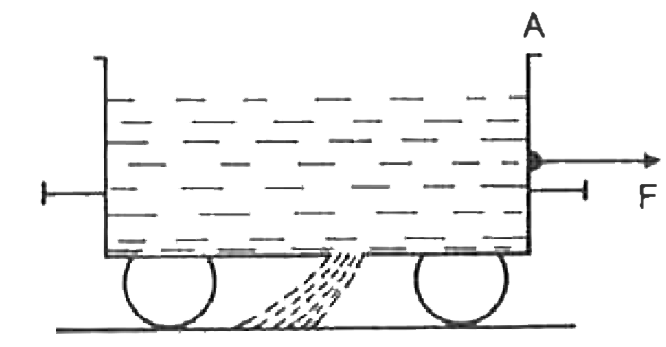
Find an expression for, the acceleration and speed of a trolley A under the action of a constant force F if it contains sand that pours out through the floor at the rate of μ per second. The speed of the trolley at t=0 was v=0 and the initital mass of sand and trolley was M0
 View Solution
View SolutionQuestion 41
A body of mass m is drawn up a smooth inclined plane (Figure 5.21) of height h and length l by means of a string passing over the vertex of the plane. From the other end of the string hangs a mass m'. Show that in order that m may just reach the top of the plane, m' msut be deteched after m has moved through a distance m+m'm'hlh+l
 View Solution
View SolutionQuestion 46
A rope is stretched between two stationary boats on the surface of a lake. A man in the first boat pulls the rope with a constant force of 100 N. The distance between the boats is 100 m in the beginning. The mass of the first boat with the man is 250 kg ,while the mass of the other is 500 kg. Find :(i) the velocity of approach of the two boats 15 s after the start,(ii) the time taken for the two boats to meet each other. [Hint: Consider relative acceleration and apply kinematic equations.]View SolutionQuestion 48
A mass M attached to the end of a small flexible rope of diameter d=1 cm is raised vertically by winding the rope on a reel. If the reel is turned uniformly ay the rate of n=2 rps, what will be the tension T in the rope? Neglect inertia of the rope and slight lateral motion of the suspended mass. (Fig.5.25)
 View Solution
View SolutionQuestion 51
A simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being 2√5
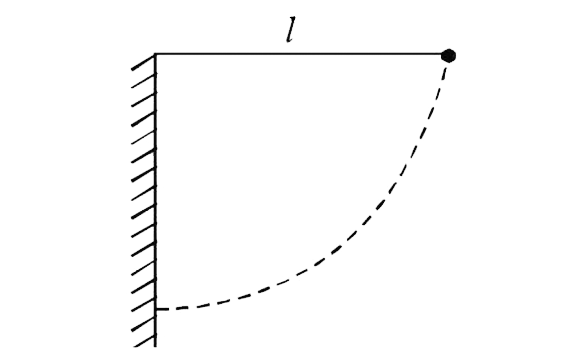
what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ? View SolutionQuestion 52
A small metal ball falls vertically and strickes a smooth plane inclined at an angle θ to the horizontal (θ<45∘). The ball rebounds horizontally. Show that a fraction (l-e) of the kinetic energy is lost during the impact and that if m is the mass and μ the speed of the ball before impact, the impulse on the plane is μsecθ. Here e isi the coefficient of restitutuon. View SolutionQuestion 56
A particle of mass 1.0g moving with velocity v1=3.0i−2.0j experiences a perfectly inelastic collision with another particle of mass 2.0g and velocity v2=4.0j−6.0k. Find the velocity of the formed particle (both the vector v and its modulus), if the components of the vectors v1 and v2 are given in the SI units. View SolutionQuestion 57
A ball moving translationally collides elastically with another, stationary, ball of the same mass. At the moment of impact the angle between the straight line passing through the centres of the balls and the direction of the initial motion of the striking ball is equal to α=45∘. Assuming the balls to be smooth, find the fraction η of the kinetic energy of the striking ball that turned into potential energy at the moment of the maximum deformation. View SolutionQuestion 59
To raise a weight which is half as much again as his weight a man fastens a rope to it and passes over a smooth pulley, he then climbs up the rope with an acceleration 6g7 relative to the rope. Show that the weight rises with acceleration 87, and find the tension of the rope.View Solution