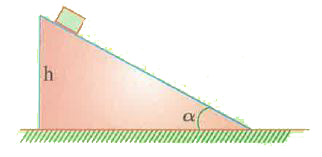
A body of mass m is drawn up a smooth inclined plane (Figure 5.21) of height h and length l by means of a string passing over the vertex of the plane. From the other end of the string hangs a mass m'. Show that in order that m may just reach the top of the plane, m' msut be deteched after m has moved through a distance m+m'm'hlh+l
The correct Answer is:N//a
Topper's Solved these Questions
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (A)
27 Videos
- KINETIC THEORY OF GASESBOOK - NN GHOSHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions
24 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
Similar Questions
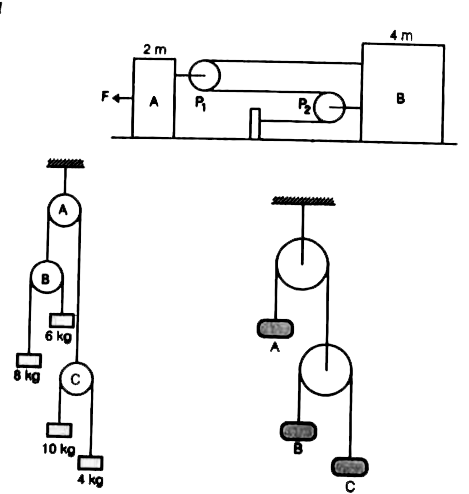
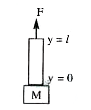
A vertical force of magnitude Facts at the top of a string of mass 'm' and length 'l'. A body of mass M hangs at the bottom of the string.
View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View Solution
Knowledge Check
A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
Am0BmCm2Dm−1An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
A body of mass m is released from the top of a rough inclined plane of length l and height h If f is the force of friction prove that the body will reach the bottom with a velocity υ=√2m(mgh−fl) .
View SolutionA mass m slides down a smooth inclined plane of inclination α and draws another mass from rest through a distance d meter in t second along a smooth horizontal table which is on level with the top of the plane over which the string passes. Find m' /m.
View SolutionA mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is μ.
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

View SolutionA block of mass 2 m hangs by an inextensible light string that passes over a smooth pulley. Another mass m hangs from the other end of the string and is connected to a vertical massless spring. The system is stationary. Just after the string is cut, the accelerations of m and 2m, respectively, are -

View Solution
