A circular spring of natural length l0 is cut and weided with two beads of masses m1andm2 such that the ratio of the lengths of the springs between the beads is 4:1 if the stiffness of the spring is k. find the frequency of oscillation of the beads in a smooth horizontal rigid tube. Assume m_(1) = m and m_(2) = 3 m.

When m1 is displaced x, each spring will be deformedby same amoun. Hence, the springs are connected in parallel. The equivalent spring constant is
keq=k1+k2

If the spring is cut, the force constant of spring
k∝1l⇒k1l1=k2l2=kl
Substituting l1=l/5andl2=4/5, we have
k1=5kandk2=54k
Then keq=254k
Now we have two partical of masses m1andm2 and one spring of stiffness
keq=254k
The reduced mass is μ=m1m2(m1+m2)
where m1=mandm2=3m
This gives μ=3/4m
Substituting μ=3/4mandkeq=25/4k in the formula
ω=√keqμ⇒ω=
⎷254k34m=√25k3m=5√k3m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
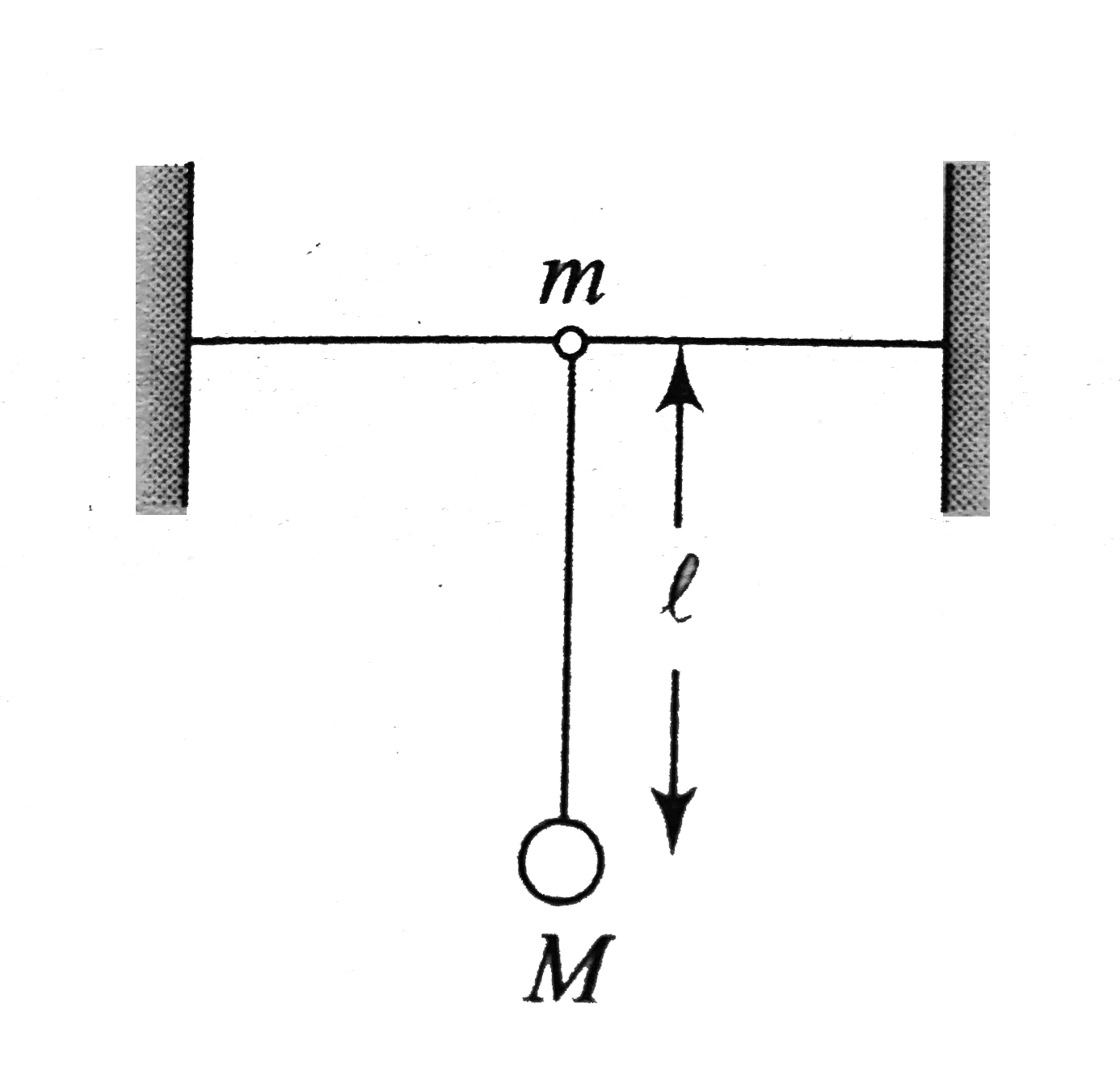
A smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View Solution
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. Te frequency of small oscillation is .
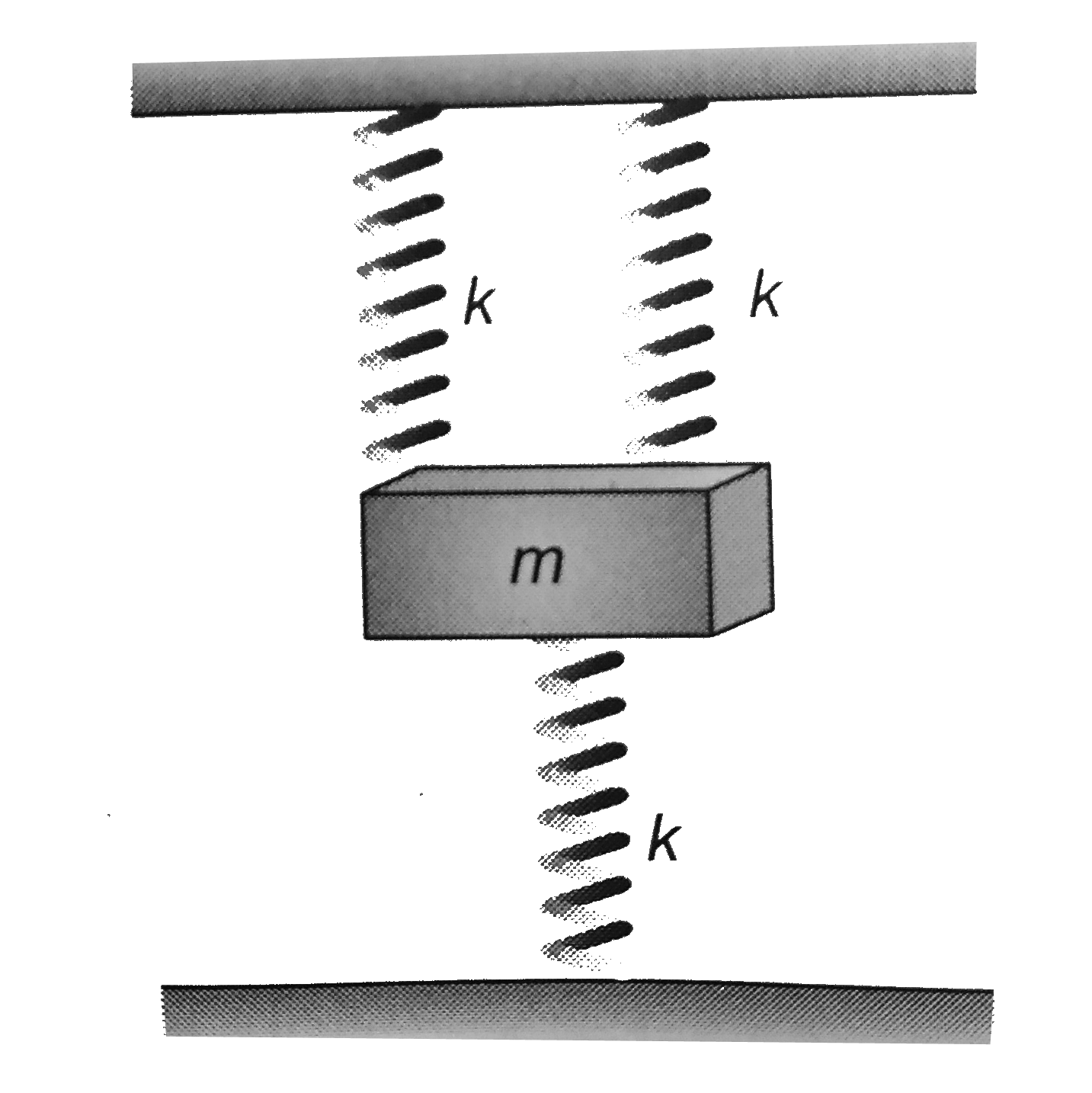
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View SolutionA spring connects two particles of masses m1andm2 A horizontal force F acts on m1 Ignoring friction, when the elongation of the spring is x then:

View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

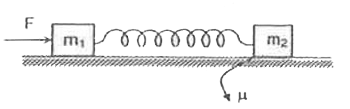
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View Solution
