Subjective from CENGAGE PHYSICS (ENGLISH) Chapter 13 LINEAR AND ANGULAR SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | LINEAR AND ANGULAR SIMPLE HARMONIC MOTION |
| CENGAGE PHYSICS (ENGLISH) | Subjective |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
A rectangular tank having base 15cm×20cm is filled with water (density ρ=1000kg/m3) up to 20cm and force constant K=280N/m is fixed to the bottom of the tank so that the spring remains vertical.
This system is in an elevator moving downwards with acceleration a=2m/s2. A cubical block of side l=10cm and mass m=2kg is gently placed over the spring and released gradually, as shown in the figure.

a. Calculate compression of the spring in equilibrium position.
b. If the block is slightly pushed down from equilibrium position and released, calculate frequency of its vertical oscillations.View SolutionQuestion 3
A body A mass m1=1kg and body B of mass m2=4.1kg. The body A perform free vertical harmonic oscillations with the amplitude 1.6cm and frequency 25Hz. Neglecting the mass of the spring , find the maximum and m inimum value of force that the system exerts on the hearing surface.
 View Solution
View SolutionQuestion 4
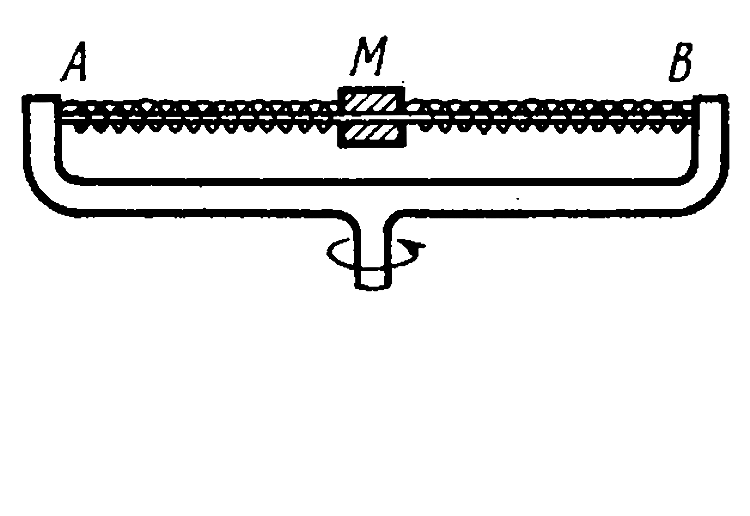
In the arrangement shown in figure the sleeve M of mass m=0.20kg is fixed between two identical springs whose combined stiffness is equal to x=20N/m. The sleeve can slide without friction over a horizontal bar AB. The arrrangement rotates with a constant angular velocity ω=4.4rad/s about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve ?
 View Solution
View SolutionQuestion 5
A vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
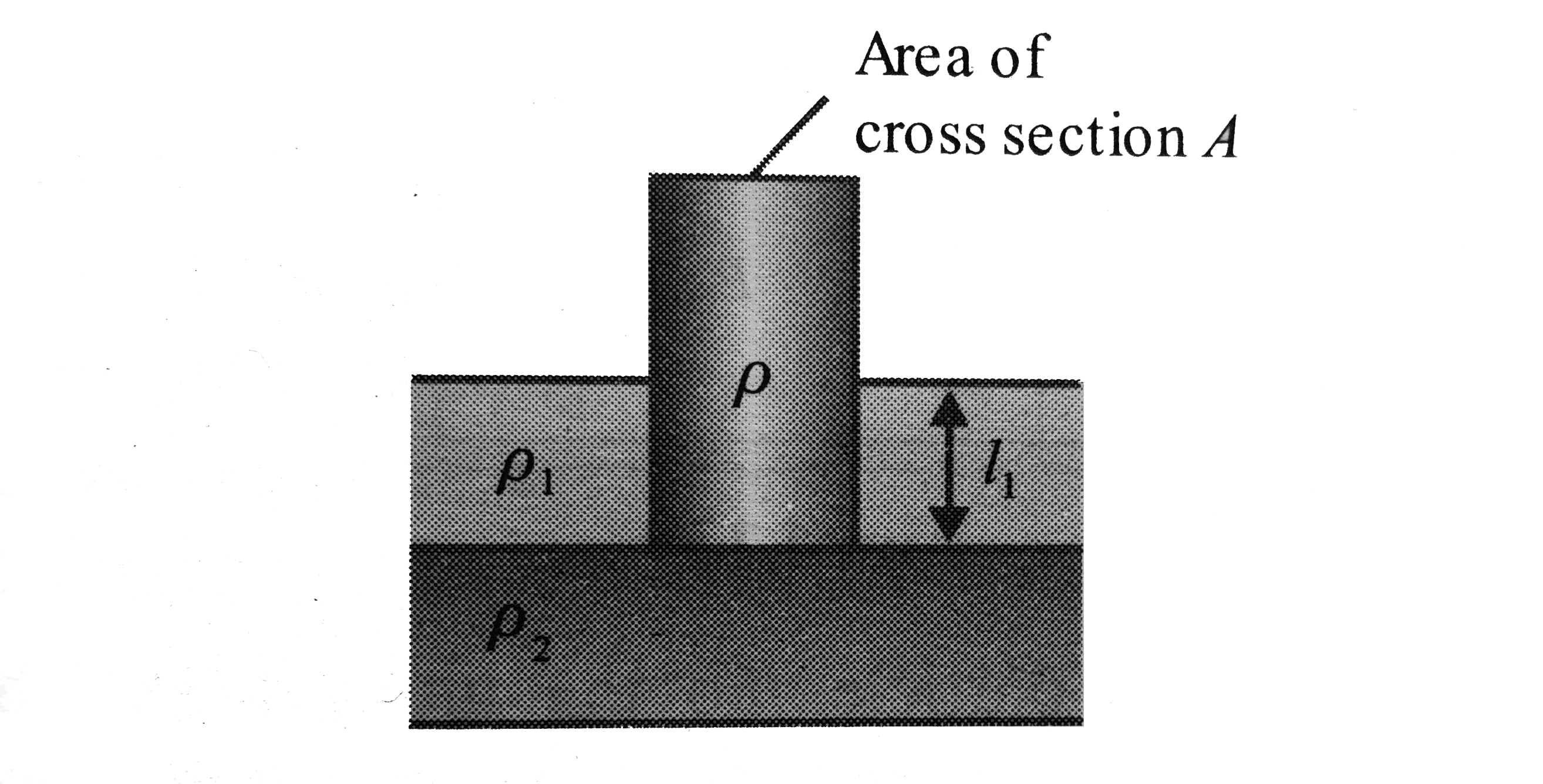 View Solution
View SolutionQuestion 6
In the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock m2 is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?View SolutionQuestion 7
A uniform dise of mass m and radius R is connected with two light springs 1 and 2. The springs are connected at the highest point M and the CM 'N' of the dise. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontalby a small distance , the discoscillates simple harmonically. Assuming a perfect rolling of the dise on the horizontal surface , find the angular frequency of oscillation.
 View Solution
View SolutionQuestion 9
A partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates xasU(x)=Ax2−Bx where A and B are positive constant.
Find the time period of small oscillation that the partical perform about equilibrium possition.View SolutionQuestion 10
A particle of mass 2kg is moving of a straight line under the actin force F=(8−2x)N. It is released at rest from x=6m.
a. Is the partical moving simple harmonically.
b.Find the equilibrium position of the particle.
c. Write the equation of motion of the partical.
d. Find the time period of SHM.View SolutionQuestion 11
A body of mass m hangs from a smooth fixed pulley P1 by the inextensible string fitted with the springs of stiffness k1 and k2 . The string passes over the smooth light pulley P2 which is connected with another ideal spring of stiffness k2. Find the period of oscillation of the body.
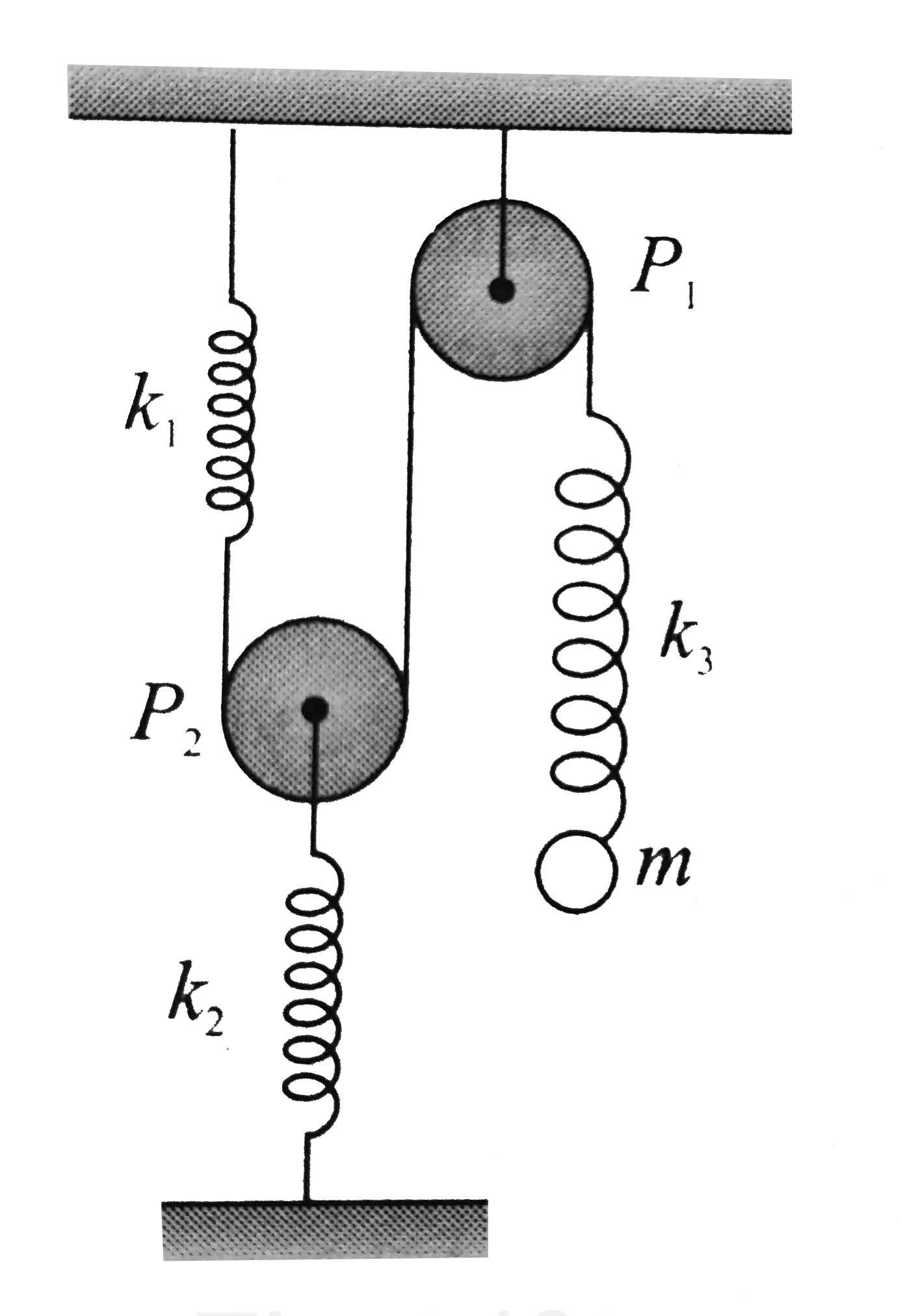 View Solution
View SolutionQuestion 14
A stepped dies of mass M and radius R is pivoted at its center C smoothly. An inextensible string connected with a light spring of stiffness k passes over the pulley. One end of the string is rigidly connected with the ground and the other end is attached to a body of mass m . If the string does not slide on the pulley, find the angularfrequency of oscillation of the syytem
 View Solution
View SolutionQuestion 16
A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (ρ) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the frequency of oscillation of the cylinder is.View SolutionQuestion 21
In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A partical of mass m is released from height 4.5mg/k from 2m . The partical stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
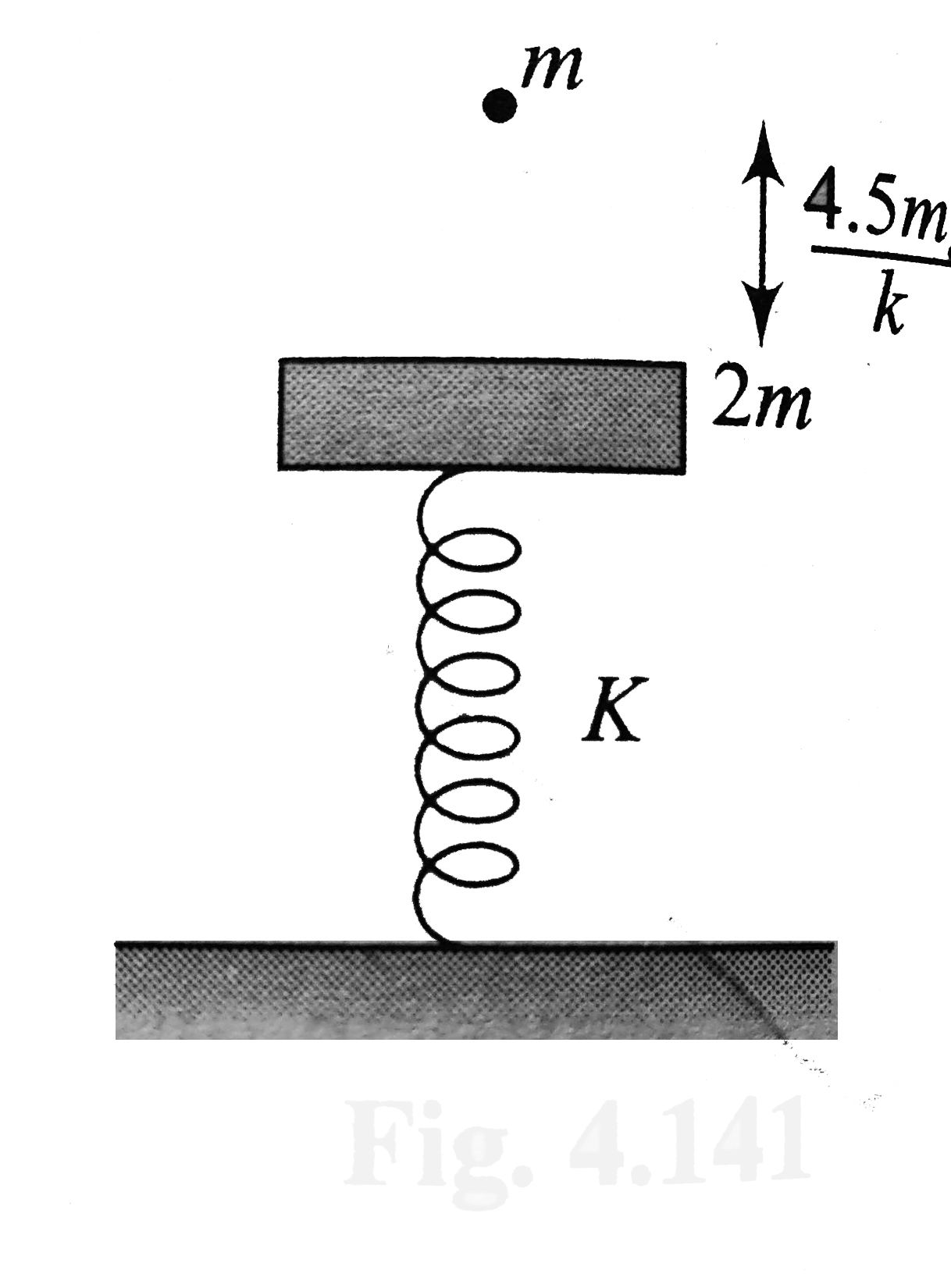 View Solution
View Solution