Integer from CENGAGE PHYSICS Chapter 27 WORK, POWER & ENERGY for Class 11
| Class 11 | PHYSICS |
| Chapter | WORK, POWER & ENERGY |
| CENGAGE PHYSICS | Integer |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
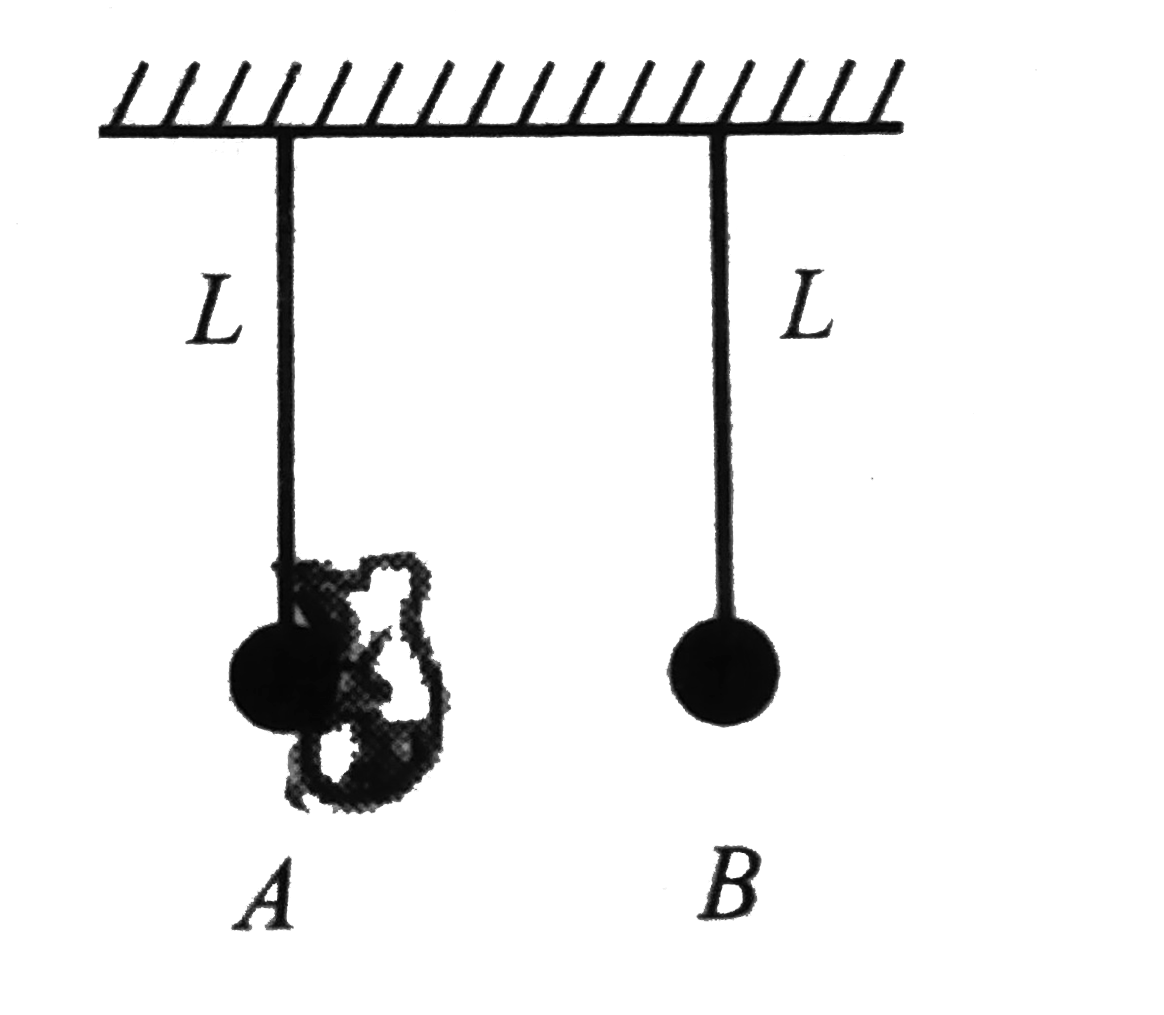
An insect jumps from ball A onto ball B, which are suspended from inextensible light strings each of length L=8cm. The mass of each ball and insect is same. What should be the minimum relative velocity (in ms−1) of jump of insect w.r.t. ball A, if both the balls manage to complete the full circle?
 View Solution
View SolutionQuestion 4
A block of mass m=0.14kg is moving with velocity v0 towards a mass less unstretched spring of force constant K=10Nm−1. Coefficient of friction between the block and the ground is μ=1/2.

Find the maximum value of compression in the spring (in cm), so that after pressing the spring the block does not return back but stops there permanently.View SolutionQuestion 6
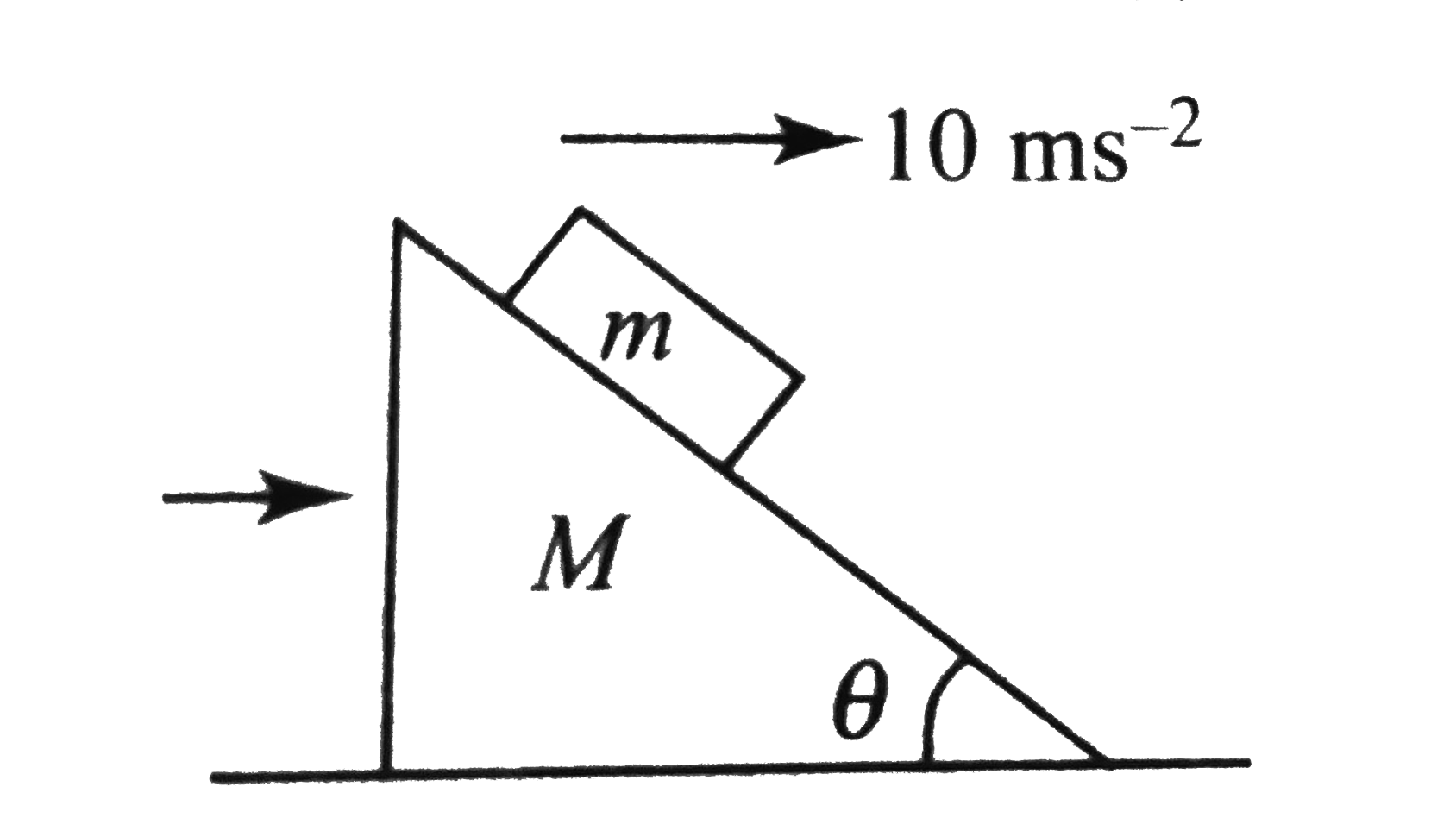
In figuer, shown all the surfaces are frictionless, and mass of the block is m=100g. The block and the wedge are held initially at rest. Now the wedge is given a horizontal acceleration of 10ms−2 by applying a force on the wedge, so that the block does not slip on the wedge. Then find the work done in joules by the normal force in ground frame on the block in 1s.
 View Solution
View SolutionQuestion 9
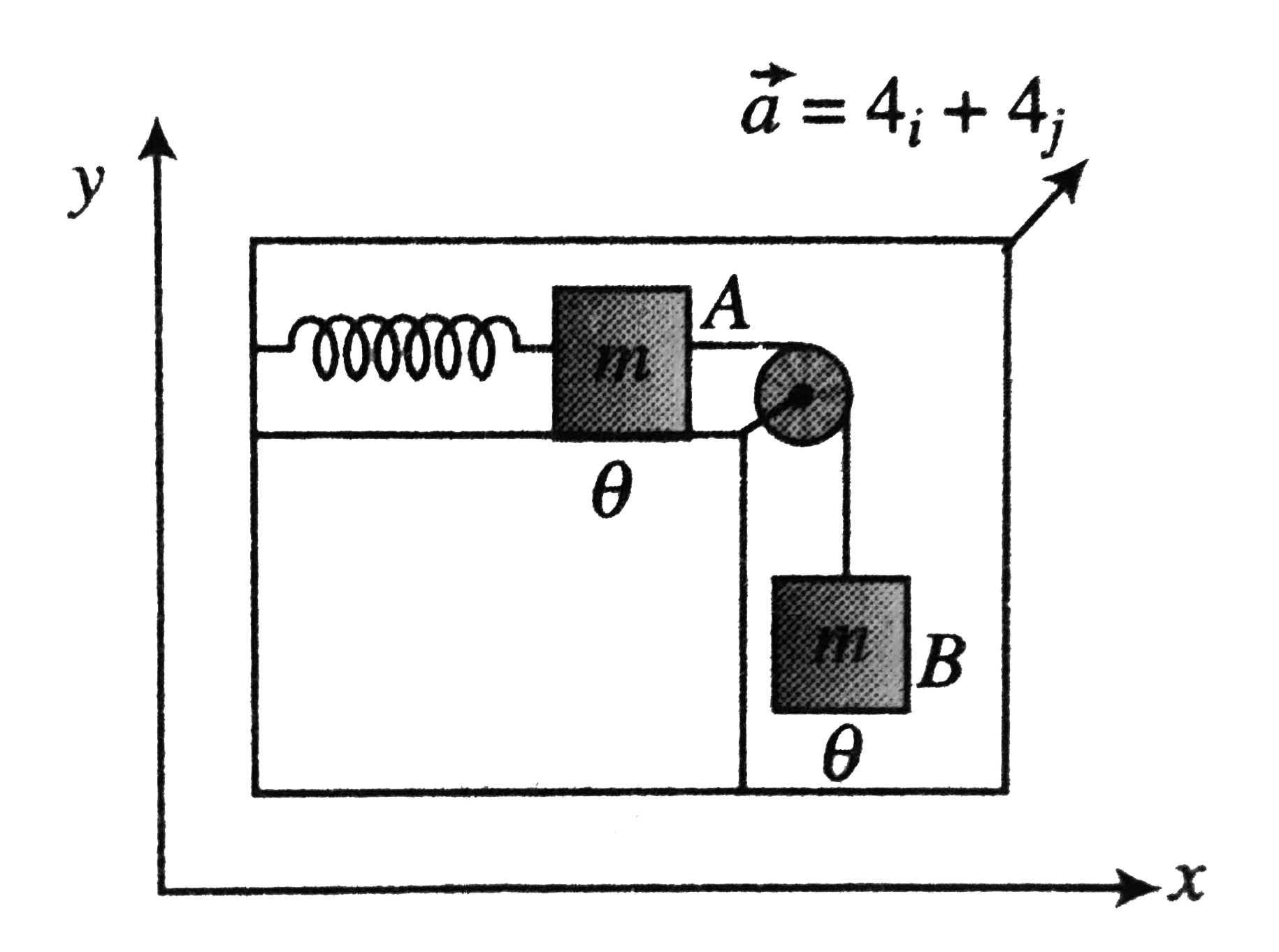
The arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in (cm) of the spring. (g=10ms−2).
 View Solution
View SolutionQuestion 11
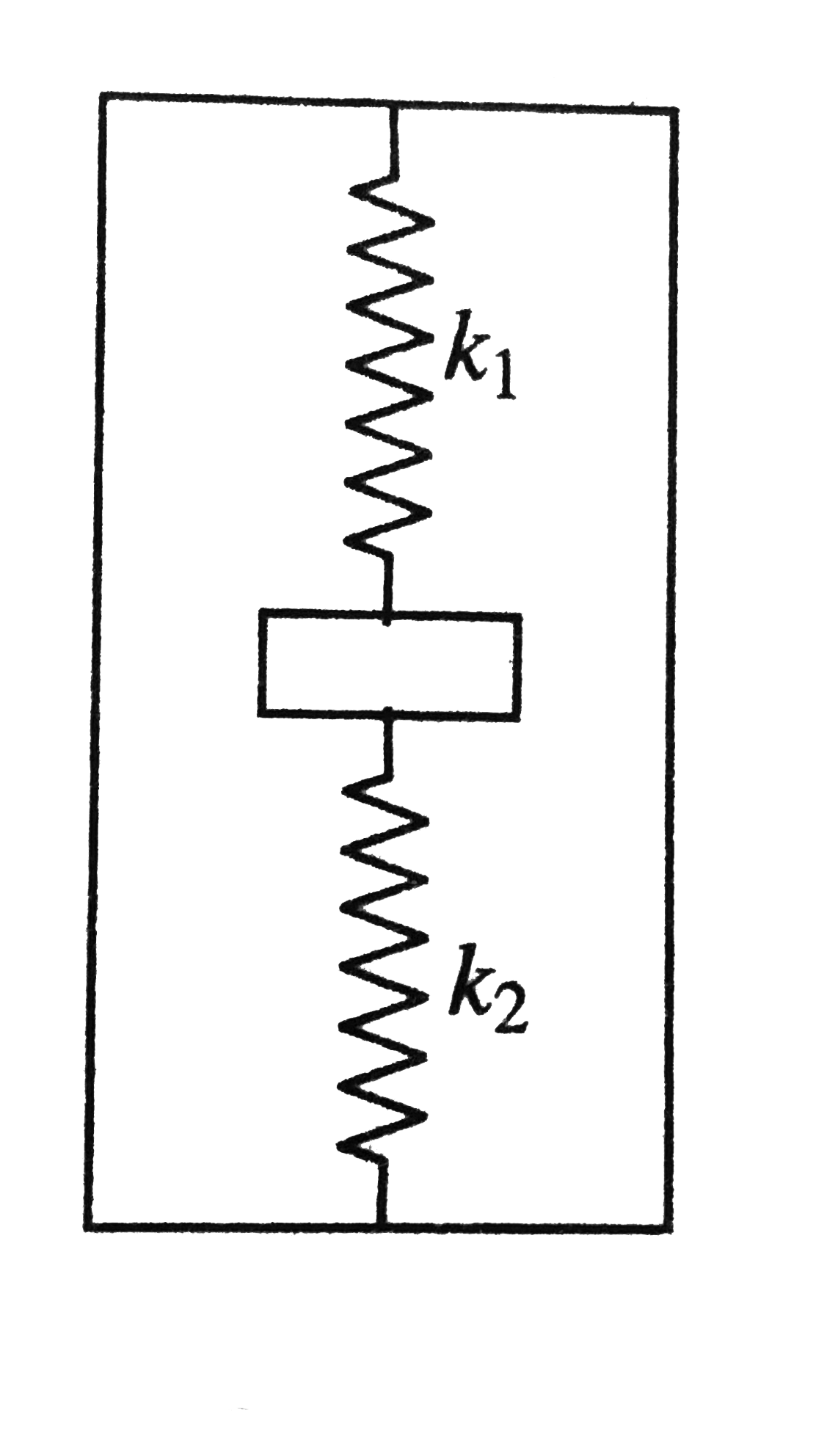
One end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
 View Solution
View SolutionQuestion 12
A system consists of two identical cubes, each of mass 3kg, linked together by a compressed weightless spring of force constant 1000Nm−1. The cubes are also connected by a thread which is burnt at a certain moment. At what minimum value of initial compression x0 (in cm) of the spring will the lower cube bounce up after the thread is burnt together?
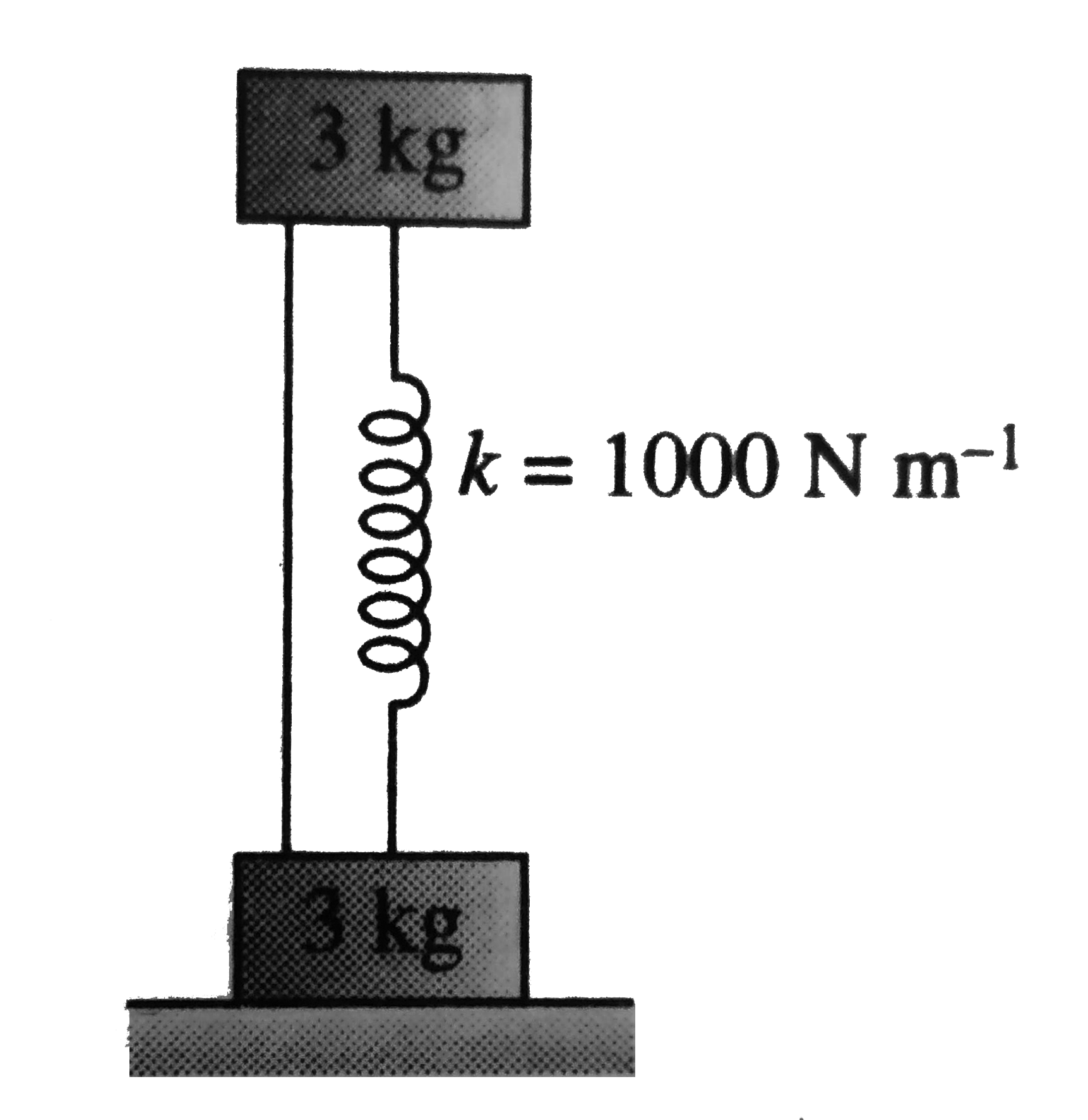 View Solution
View SolutionQuestion 13
A particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
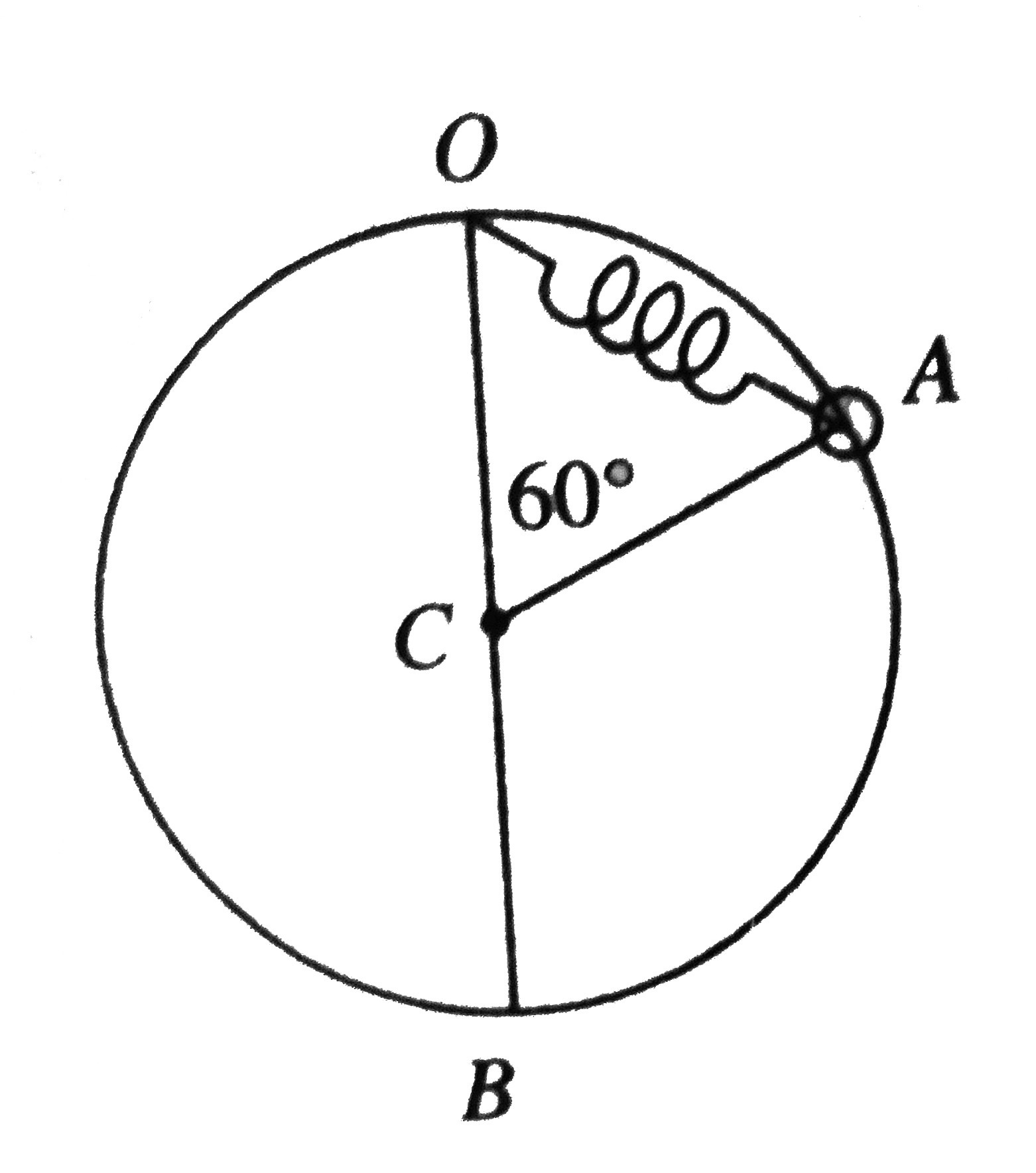 View Solution
View SolutionQuestion 14
A 2144kg freight car roles along rails with negligible friction. The car is brought to rest by a combination of two coiled springs as illustrated in figure. Both springs are described by Hooke's law with k1=1600Nm−1 and k2=3400Nm−1. After the first spring compresses a distance of 30.0cm, the second spring acts with the first to increase the force as additional compression occurs as shown in the graph in figure. The car comes to rest 50.0cm after first contracting the two-spring system. Find the car's initial speed (in×10−1Nm−1).
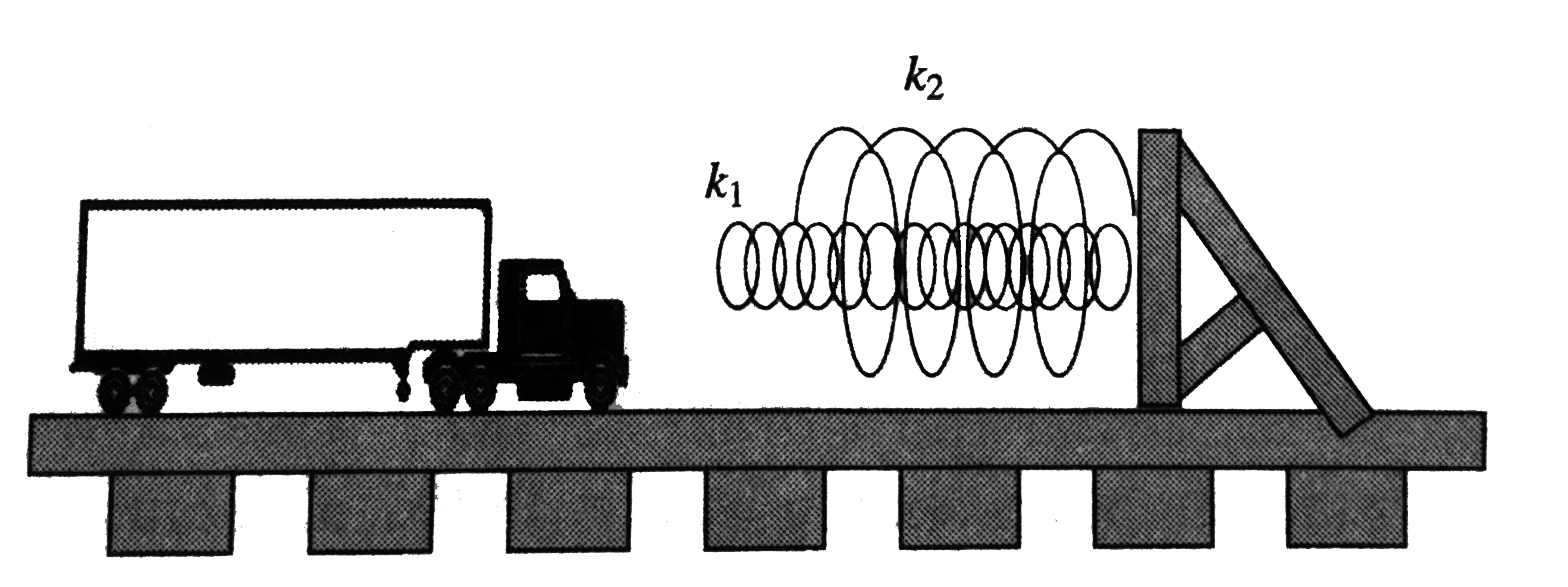
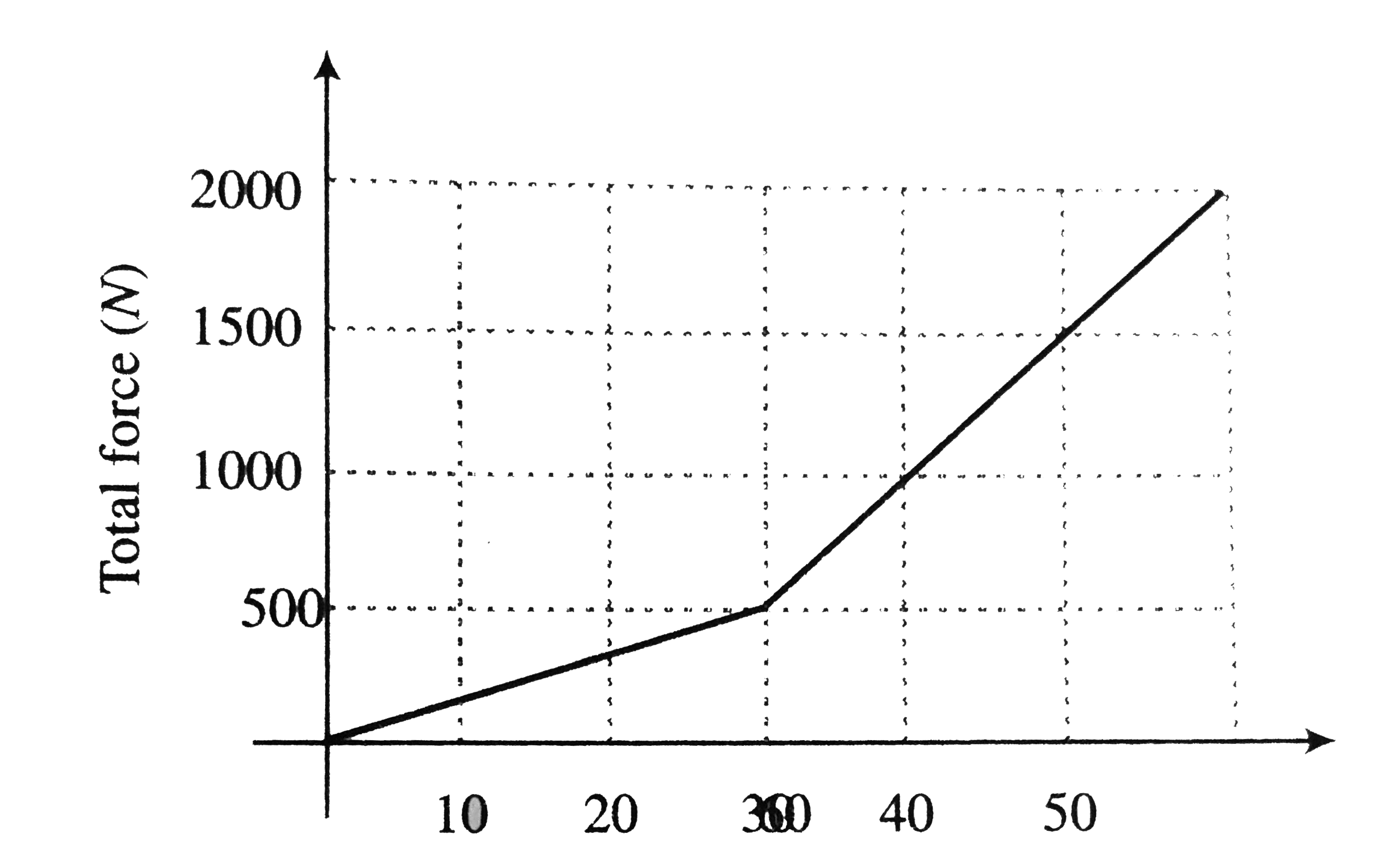 View Solution
View Solution