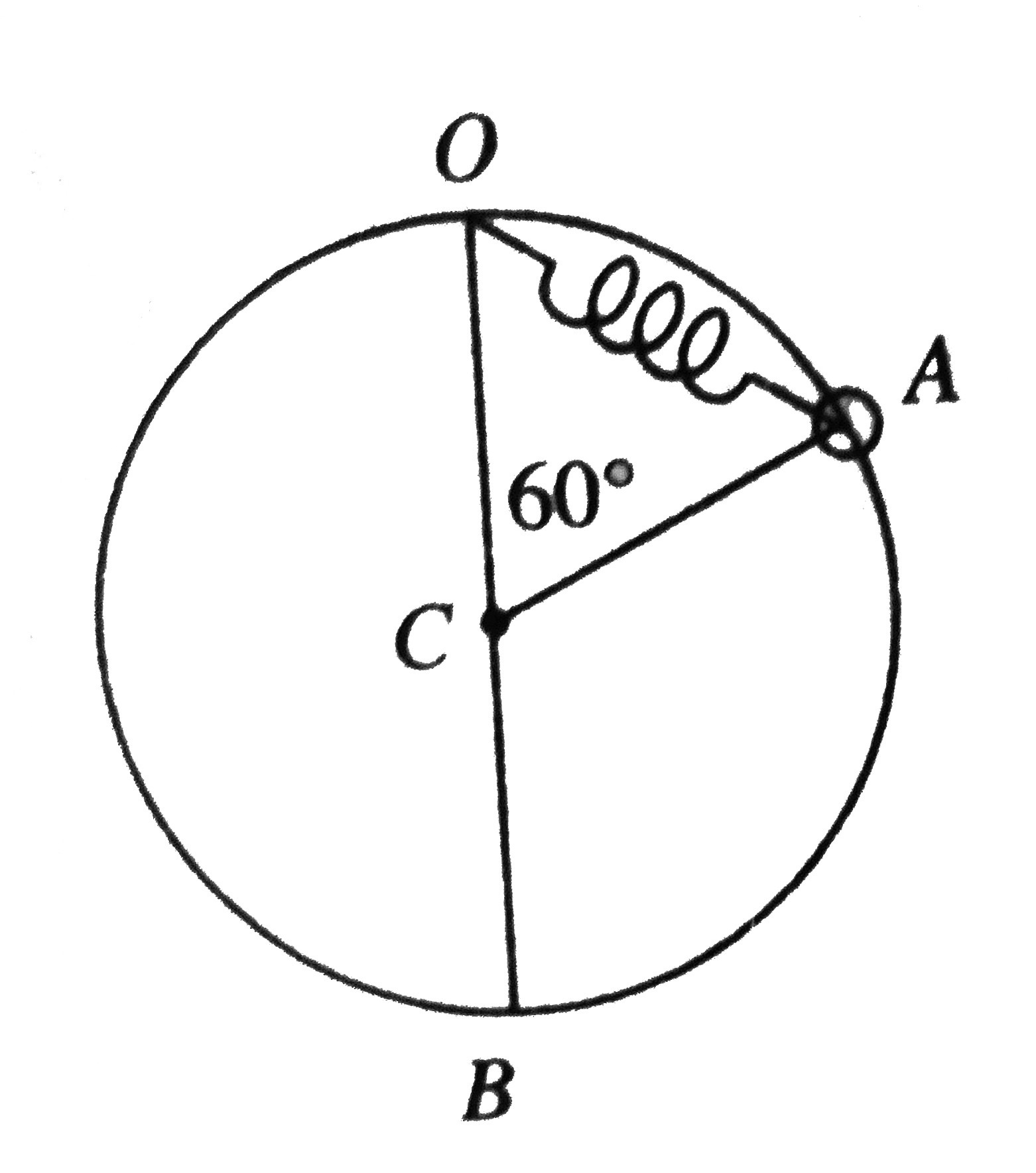
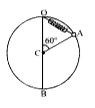
A particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
The correct Answer is:(5)
According to conservation of energy between A and B, loss in gravitational potential energy=gain in elastic potential energy + gain in KE
mg(r2+r)=12k(2r−r)2+12mv2 (i)
At point B, centripetal force equation is
kr−mg=mv2r (ii)
Solving Eqs. (i), and (ii), we get k=500Nm−1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )19videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)3videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
If maching is lubricated with oil
12:25View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit −ϕ and +ϕ. For an angular displacement θ(|θ|<ϕ), the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
05:04View SolutionTwo unequal masses are ties together with a cord with a compressed spring in between.
When the cord is burnt with a match releasing the spring, the two masses fly apart with equal09:54View SolutionWhich of the following statements is/ are correct(Figure)
 View Solution
View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R//4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60^@ with the vertical. The spring constant K=mg//R . Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.
04:46View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.01:49View SolutionA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=((sqrt3+1)mg)/R' . The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
14:14View SolutionA small particle of mass m is fixed to the perimeter of a ring of same mass and radius r. The system comprising of particle and ring is placed on a horizontal plane. Friction is negligible on horizontal plane. Initially particle is at top most point, then the system is released from rest. Answer next two question when the particle is at the same height as the centre of ring aftr being released from top most point. Assume that the ring stays in vertical plane during its motion under consideration

Mark the CORRECT option(s):13:40View SolutionA small particle of mass m is fixed to the perimeter of a ring of same mass and radius r. The system comprising of particle and ring is placed on a horizontal plane. Friction is negligible on horizontal plane. Initially particle is at top most point, then the system is released from rest. Answer next two question when the particle is at the same height as the centre of ring aftr being released from top most point. Assume that the ring stays in vertical plane during its motion under consideration

Mark the CORRECT option(s):-07:19View SolutionA point particle of mass m is released from a distance sqrt(3)R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
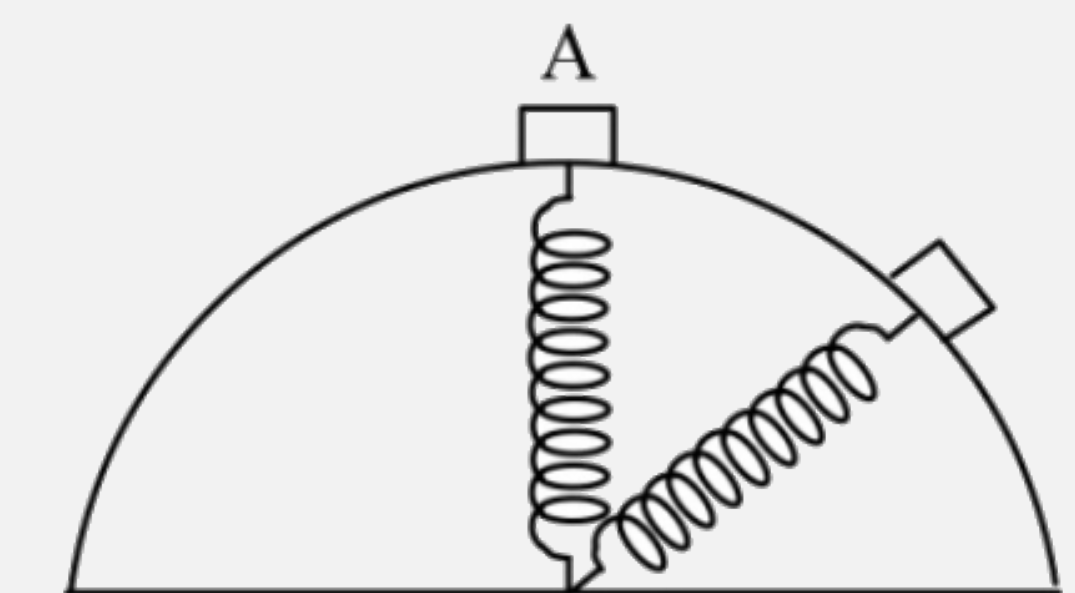
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
 07:05View Solution
07:05View SolutionConsider two identical rings of mass M and radius R fixed on a horizontal axis in a gravity - free space. A particle of mass m is held at rest at the centre of 1^("st") ring and projected along the axis towards 2^("nd") ring. The minimum speed of projection so that the particle reaches the centre of 2^("nd") ring is
12:35View Solutionएक चिकने अर्धवृत्ताकार आकृति की R त्रिज्या वाली तार की ऊर्ध्व तल में स्थित है। लीक के निम्नतम बिन्दु O पर 3R4 स्वाभाविक लम्बाई की एक भारहीन स्प्रिंग का एक सीरा जुड़ा है। स्प्रिंग का दूसरा सीरा m द्रव्यमान के एक छल्ले बिन्दु P पर स्थितरावस्था में है तब स्प्रिंग उर्ध्व से 60∘ का कोण बनाती है। स्प्रिंग नियतांक k=mg/R है। जब छल्ले को मुक्त किया जाता है तब
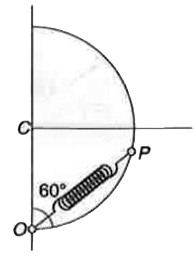
(a) छल्ले का बल निर्देशांक आरेख बनाइये।
(b) छल्ले के स्पर्शरेखीय त्वरण तथा अभिलम्ब प्रतिक्रिया के मान ज्ञात कीजिए।05:06View SolutionOne end of a spring of spring constant 80 Nm^(-1) and unstretched length of 30 cm is fixed at point A and the other end of the spring is fitted with a smooth ring of mass 300g as shown in the figure. The rings is allowed to slide on a horizontal rod fixed at a height of 40 cm. Initially the spring makes an angle of 60^(@) with the vertical and the system of spring and ring is released from rest. The speed of the ring when the spring becomes verticcal is _______ ms^(-1) .
06:16View Solution5kg द्रव्यमान का एक कण ऊर्ध्वाधर तल में r=20 से० मी० की एक दृढ़ चिकनी वलय जिसकी त्रिज्या r=20cm पर मुक्त रूप से फिसलता है। कण, स्प्रिंग जिसका दूसरा सिरा वलय के शीर्षतम बिंदु O से दृढ़ है, के एक सिरे से संयोजित है। प्रारम्भ में कण वलय के बिंदु A पर इस प्रकार विरामावस्था में है की ∠OCA=60∘, C वलय का केंद्र है । स्प्रिंग की प्रकृतिक लम्बाई r=20cm के बराबर है । कण को मुक्त होकर तथा नीचे फिसलने के पश्चात जब यह निम्नतम स्थिति B तक पहुंचता है कण व वलय के मध्य सम्पर्क बल शून्य हो जाता है । स्प्रिंग का बल नियतांक ज्ञात कीजिये ।
 02:55View Solution
02:55View Solution

