Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO from GK PUBLICATIONS PHYSICS (HINGLISH) HEAT TRANSFER for Class 12
| Class 12 | PHYSICS |
| Chapter | HEAT TRANSFER |
| GK PUBLICATIONS PHYSICS (HINGLISH) | Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A compound rod is formed of a steel core of diameter 1cm and outer casing is of copper, whose outer diameter is 2cm. The length of this compound rod is 2m and one end is maintained as 100∘C and the end is at 0∘C. If the outer surface of the rod is thermally insulated, then heat current in the rod will be (Given thermal conductivity of steel j=12cal/m/k/s, thermal conductivity of copper =92cal/m/k/sView SolutionQuestion 3
A steel boiler whose thickness is 3 cm is placed on a plate of area 1m2. The temperature of the plate is 300∘C and that of the boiling water in the boiler is 100∘C. How much water will evaporate per minute? (Conductivity of steel =63.0Js−1m−1K−1 and sp. latent heat of vaporisation of water =2251.2×103Jkg−1.)View SolutionQuestion 4
A certain double plane window consists of two glass sheets each 80cm×80cm×0.30cm, separated by 0.3cm stagnant air space between them (see figure-4.49). The indoor surface temperature is 20∘C, while the outdoor surface temperature is 0∘C. Find:
(a) the temperature of the surface of the sheets in contact.with the stagnant air
(b) the power transmitted from the inside to the outside. Given that Kglass=2.0×10−3cals−1cm−1∘C ,
Kair=2.0×10−4cals−1cm−1∘C−1
 View Solution
View SolutionQuestion 5
Water is being boiled in a flat bottomed kettle placed on a stove The area of the bottom is 300cm2 and the thickness is 2mm If the amount pf steam produced is 1gm−1min then the difference of the temperature between the inner and the outer surface of the bottom is (thermal conductivity of the matrial of the kettle 0.5calcm−1C−1 latent heat of the steam is equal to 540calg−1) .View SolutionQuestion 7
Some water is placed in a container made ofa material of poor thermal conductivity. Temperature of water in it is 520 K. The total wall area of the container is 8000cm2. The surrounding temperature is 300 K. Find the rate at which heat current will flow from atmosphere to water.View SolutionQuestion 8
Heat is conducted through a slab composed of paralel layers of two different materials of conductivities 134.4 SI units and 58.8 SI units and of thickness 3.6cm and 4.2cm respectively. The temperature of the outer faces of the compound slab are 96∘C and 8∘C. Find (i) the temperature of the interface, (ii) temperature gradient in each section of the slab.View SolutionQuestion 9
Two bodies each of mass m, having specific heats s, are connected by ametal rod of negligible heat capacity of length l, area of cross section A and thermal conductivity k. Initially both bodies are at different temperatures, find the time taken for the temperature difference between the two bodies to become half of the. initial value.View SolutionQuestion 10
A 2 m long wire of resistance 4Ω and diameter 0.64 mm is coated with plastic insulation of thickness 0.66 mm. A current of 5A flows through the wire. Find the temperature difference across the insulation in the steady state. Thermal conductivity of plastic is 0.16×(10−2)cal/scm.∘C.View SolutionQuestion 11
One end of a steel rod of length 1 m and area of cross section 4×10−6m2 is put in boiling water and the other end is kept in an ice bath at 0∘C. If thermal conductivity of steel is 46W/m∘C, find the amount of ice melting per second if heat flow only by conduction. Given that the latent heat of fusion of ice is 3.36×105J/kg.View SolutionQuestion 13
The heat generated by radioactivity within the earth is conducted outward through the oceans. Assuming the average temperature gradient within the solid earth beneath the ocean to be 0.07∘C−1 and the average thermal conductivity 0.2calm−1s−1^(∘)C−1, determine the rate of heat transfer per square metre. Radius of the earth = 6400 km.- further, determine the quantity of heat transferred through the earth's surface each dayView SolutionQuestion 14
Two rods whose lengths are l1 and l2 and heat conductivity coefficient x1 and x2 are placed end to end. Find the heat conductivity coefficient of a uniform rod of length l1+l2 whose conductivity is the same as that of the system of these two rods. The lateral surfaces of the rods are assumed to be thermally insulated.View SolutionQuestion 15
A solid copper sphere (density =8900kgm−3 and specific heat C=390Jkg−1K−1) of radius r=10cm is at an initial temperature T1=200K. It is then suspended inside an chamber whose walls are at almost OK. Calculate the time required for the temperature of the sphere to drop to T2=100K, σ=5.67×10−8Wm−2K−4.View SolutionQuestion 16
A calorimeter of mass 100 g contains 100cm3 of water at 70∘C. It cools down to 30∘C in 12 minutes. When the same volume of glycerine is used in the same calorimeter, it takes 8 minutes to cool down through the same temperature range. Find the specific heat of glycerine of specific heat of the calorimeter is 0.1calg−1^(∘)C−1 and specific gravity of glycerine =1.27.View SolutionQuestion 17
A vertical brick duct (tube) is filled with cast iron. The lower end of the duct is maintained at a temperature T1 which is greater than the melting point Tm of cast iron and the upper end at a temperature T2 which is less than the temperature of the melting point of cast iron. It is given that the conductivity of liquid cast iron is equal to k times the conductivity of solid cast iron. Determine the fraction of the duct filled with molten metal.View SolutionQuestion 18
The gas between two long coaxial cylindrical surfaces is filled with a homogeneous isotropic substance. The radii of the surfaces are r1=5.00cm and r2=7.00cm. In the steady state the temperatures of the inner and outer surfaces are T1=290Kand=320K respectively. Find the temperature of a coaxial surface of radius r.View SolutionQuestion 19
The tungsten filament of an electric lamp has a length l=0.25m and diameter d=0.04mm. The power rating is P=100W. Assuming the radiation from the filament to be η=80% of that of a black body radiator at the same temperature, estimate the temperature of the filament. Stefan constant =5.7×10−8W/m2K4.View SolutionQuestion 20
There are two concentric metallic shells of negligible thickness of radii 5 cm and 20 cm. The region between the two shells is filled with a medium of thermal conductivity k. The temperature of inner and outer sphere is maintained at 5∘C and 10∘C respectively. If the heat current flowing from inner to outer sphere is 100 W, find the value of k.View SolutionQuestion 21
Two bodies A and B ahave thermal emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are the same. The two bodies emit total radiant power of the same rate. The wavelength λB corresponding to maximum spectral radiancy in the radiation from B shifted from the wavelength corresponding to maximum spectral radiancy in the radiation from A, by 1.00μm. If the temperature of A is 5820K:View SolutionQuestion 22
A thin brass rectangular sheet of sides 15.0 and 12.0 cm is heated in a furnace to 600∘ C and taken out. How much electric power is needed to maintain the sheet at this temperature, given that its emissivity is 0.250?
Neglect heat loss due to convection (Stefan-Boltzmann constant, σ=5.67×10−8W/m2−K4).View SolutionQuestion 24
Over what distance must there be heat flow by conduction from the blood capillaries beneath the skin to the surface if the temperature difference is 0.50∘C ? Assume 200W must be transferred through the whole body's surface area of 1.5m2 Given that thermal conductivity of blood cells is 0.2W/mK.View SolutionQuestion 25
A room at 20∘C is heated by a heater of resistence 20 ohm connected to 200 VV mains. The temperature is uniform throughout the room and the heati s transmitted through a glass window of area 1m2 and thickness 0.2 cm. Calculate the temperature outside. Thermal conductivity of glass is 0.2cal/mC∘ s and mechanical equivalent of heat is 4.2J/cal.View SolutionQuestion 26
Assume that a planet radiates heat at a rate proportional to the fourth power of its surface temperature T and that the temperature of the planet is such that this loss is exactly compensated by the heat gained from the sun. Show that other things remaining the same, a planet's surface temperature will vary inversely as the square root of its distance from the sun.View SolutionQuestion 28
A hollow cube of metal has sides measuring 0.8cm (internal) and thickenes 0.5cm. It is filled with ice 0∘C and immersed in boiling water at 100∘C. How many kg of ice will melt in one minute? Thermal conductivity of metal =252Jm−1s−1K−1 and latent heat capacity of ic e=336×103Jkg−1.View SolutionQuestion 29
The walls of a closed cubical box of edge 50cm are mdade of a material of thickness 1mm and thermal conductivity 4×10−4 cal s−1cm−1.∘C−1 the interior of the box maintained at 100∘C above the outside temperature by a heater placed inside the box and connected acros a 400 V d.c. source. Calculate the resistance of the heater. View SolutionQuestion 30
A 300 W lamp loses all its energy by emission of radiation from the surface of its filament. If the area of surface of filament is 2.4cm2 and is of emissivity 0.4, estimate its temperature. Given that σ=1.36×10−12calcm−2s−1K−4J=4.2Jcal−1. Neglect the absorption from the surroundings.View SolutionQuestion 32
Two identical solid bodies one of aluminium and other of copper are heated to the same temperature and are put in same surrounding. If the emissivity of the aluminium body is 4 times that of copper body, find the ratio of the thermal power radiated by the two bodies. If specific heat of aluminum is 900/kg∘C and that of copper is 390J/kg∘C and density of copper is 3.4 times that of aluminum, find the ratio of rate of cooling of the two spheres.View SolutionQuestion 35
A rof of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as x=α/T, where α is a constant. The ends of the rod are kept at temperatures T1 and T2. Find the function T(x), where x is the distance from the end whose temperature is T1, and the heat flow density.View SolutionQuestion 37
A flat bottomed metal tank of water is dragged along a horizontal floor at the rate of 20ms−1. The tank is of mass 20kg and contains 1000 kg of water and all the heat produced in the dragging is conducted to the water through the bottom plate of the tank. If the bottom plate has an effective area of conduction 1 m^2 and a thickness 5 cm and the temperature of the water in the tank remains constant at 50∘C, calculate the temperature of the bottom surface of the tank, given the coefficient of friction between the tank and the floor is 0.343 and K for the material of the tank is 25calm−1s−1K−1.View SolutionQuestion 38
Two solid spheres, one of aluminium and the other of copper, of twice the radius are heated to the same temperature and are allowed to cool under the identical conditions. Given that specific heat of aluminium is 900J/kg K and that ofcopper is 390J/kg K. Specific gravity of aluminium and copper are 2.7 and 8.9 respectively.
initial rates of fall of temperature, and
the initial rates of loss of heat View SolutionQuestion 39
Estimate the rate that heat can be conducted from the interior of the body to the surface. Assume that the thickness of tissue is 4.0 cm, that the skin is at 34∘C and the interior at 37∘C, and that the surface area is 1.5m2. Compare this to the measured value of about 225W that must be dissipated by a person working lightly. This clearly shows the necessity of conveclive cooling by the blood. Given that the thermal conductivity of the blood cells is 0.2W/mKView SolutionQuestion 40
The temperature of the filament of 100−watt lamp is 4000∘C in the steady state and the radius of the glass bulb is 4 cm and the thickness of the wall is 0.4mm. Assuming that there is no convection, calculate the thermal conductivity of glass. The temperature of the outside air is 27∘C.View SolutionQuestion 41
A thin pipe having outside diameter of 3 cm is to be covered with two layers of insulation each having thickness of 2.5 cm. The thermal conductivity of one material is five times that of the other. Assuming that the inner and outer surface temperatures of the composite wall are fixed, find the percentage reduction in heat transfer when the better insulating material is next to the thin pipe than when it is outside.View SolutionQuestion 44
One end of a rod of length 20 cm is maintained at 800 K. The temperature of the other end of the rod is 750 K in steady state and this end is blackened to radiate thermal radiations like a black body. If temperature of the surrounding is 300 K, find the thermal conductivity of the rod. Assume no energy loss takes place through the lateral surface of the rod during conduction through its length.View SolutionQuestion 45
In a pitcher 10 kg water is contained.Total surlace area of pitcher walls is 2×10−2m2 and its wall thickness is 10−3m. If surrounding temperature is 42∘C, find the temperature of water in the pitcher when it attains a steady value. Given that in steady state 0.1 gm water gets evaporated per second from the outer surface of pitcher through its porous walls. The thermal conductivity of the walls of pitcher is 0.8W/m∘C and latent heat of vaporization of water is 2.27x106J/kg.View SolutionQuestion 46
A uniform copper rod 50 cm long is insulated on the sides, and has its ends exposed to ice and steam, respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.View SolutionQuestion 48
Four spheres A, B, C and D of different metals but all same radius are kept at same temperature. The ratio all their densities and specific heats are 2:3:5:1 and 3:6:2:4. Which sphere will show the fastest rate all cooling (initially) (assume black body radiation for all of them)View SolutionQuestion 49
A closed cubical box made of perfectly insulating material has walls of thickness 8 cm and the only way for heat to enter or leave the box is through two solid, cylindrical, metallic plugs, each of cross-sectional area 12cm2 and length 8 cm in opposite walls of the box. The outer surface of one plug is kept at 100∘C while the outer surface of the other plug is maintained at 4∘C. The thermal conductivity of the plug is 50cals−1m−1K−1. A source of energy generating 36cals−1 is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box, assuming that it is the same at all points on the inner surface.View SolutionQuestion 50
The solar energy received by the Earth persquare metre per minute is 8.315×104Jm−2−1min. If the radius of the Sun is7.5×105 km and the distance of the Earth from the Sun is 1.5×108 km, calculate the surface temperature of Sun. Assume the Sun as a perfect black body. Given that Stefen constanta σ=5.7×10−8Wm−2K−4. View SolutionQuestion 51
Two solid spheres are heated to the same temperature allowed to cool under identical conditions Compare (i) initial rates of fall of temperatre, and (ii) initial rates of loss of heat Assume that all the surfaces have the same emissivity and ratios of their radii specific heats and densities are respectively 1:α1:β,1:γ .View SolutionQuestion 52
A metal block with a heater in it is placed in a room at temperature 293 K. When the heater is switched on it is observed that the temperature of the block rises at the rate of 2∘C/s and when its temperature rises to 30∘C, it is switched off. Just after when heater is switched off, it is observed that the block cools at 0.2∘C/s. If Newton's law of cooling is assumed to be valid, find the power of the heater. Also find the thermal power radiated by the block when it was at 30∘C and at 25∘C. Given that the heat capacityof the block is 80J/∘C.View SolutionQuestion 53
In a cylindrical metallic vessel some water is taken and is put on a burner. The bottom surface area of the vessel is 2.5×10−3m2 and thickness 10−3m. The thermal conductivity of the metal of vessel is 50W/m∘C. When water boils, it is observed that 100 gm water is vaporized per minute. Calculate the temperature of the bottom surface of the vessel. Given that the latent heat of vaporization of water is 2.26×106J/kg.View SolutionQuestion 55
In winters ice forms on the surface of a lake. Due to abnormal expansion of water the temperature of the water at the bottom of the lake remains constant at 4∘C and we assume that the amount of heat required to maintain this temperamre of the bottom layer of water may come from the bed of the lake. If surrounding temperature is - 10∘C Prove that ice formed from the surface of the lake attains a maximum thickness. Find the maximum depth from surface upto which ice is formed if the depth of lake is I m. Given that thermal conductivity of ice is 0.5W/m∘C.View SolutionQuestion 57
The temperature of the tungsten filament of a 40 watt lamp is 1655∘C. The effective surface area of the filament is 0.85cm2. Assuming that the energy radiated from the filament is 60% of that of a black body radiator at the same temperature, find the value of Stefan's constant.View SolutionQuestion 58
A cubical tank of water of volume 1m3 is kept at a constant temperature of 65∘C by 1 KW heater. At time t=0, the heater is switched off. Find the time taken by the tank to cool down to 50∘C, given the temperature of the room is steady at 15∘C. Density of water =103kgm−3 and specific heat of water =1.0calg−1^(∘)C−1. (Do not assume average temperature during cooling). Take 1KW=240cals−1.View SolutionQuestion 62
A long tungsten heater wire is rated at 3kWm−1 and is 5.0×10−4m in diameter. It is embedded along the axis of a ceramic cylinder of diameter 0.12m. When operating at the rated power, the wire is at 1500∘C, the outside of the cylinder is at 20∘C. Find the thermal conductivity of the ceramic.View SolutionQuestion 63
A constant electric current flows along a uniform wire with cross-sectional radius R and heat conductivity coefficient x. A unit volume of the wire generates a thermal power ω. Find the temperature distribution across the wire provided the steady-state temperature at the wire surface is equal to T0.View SolutionQuestion 64
An iron boiler with walls 1.25 cm thick contains water at atmospheric pressure. The heated surface is 2.5m2 in area and the temperature of the underside is 120∘C. Thermal conductivity of iron is 20cals−1m−1K−1 and the latent heat of evaporation of water 536×103calkg−1. Find the mass of water evaporated per hour. View SolutionQuestion 66
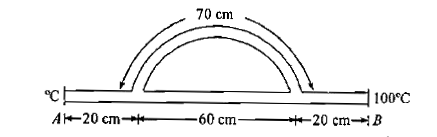
In the figure-4.51 shown here, S is a source of heat supplying energy at a constant rate 75Js−1 and S' is a sink maintained at 10∘C. The two conductors joining S to S' are each 20 cm long, 1cm2 in cross-section and of thermal conductivity 385Wm−1K−1s−1. Calculate the temperature of the point S.
 View Solution
View Solution
All Exercises from GK PUBLICATIONS PHYSICS (HINGLISH) Class 12 PHYSICS HEAT TRANSFER
- PRACTICE EXERCISE 4.1
- PRACTICE EXERCISE 4.2
- PRACTICE EXERCISE 4.3
- PRACTICE EXERCISE 4.4
- DISCUSSION QUESTION
- CONCEPTUAL MCQS SINGLE OPTION CORRECT
- NUMERICAL MCQS SINGLE OPTIONS CORRECT
- ADVANCE MCQS WITH ONE OR MORE OPTION CORRECT
- UNSOLVED NUMERICAL PROBLEMS FOR PREPARATION OF NSEP,INPHO&IPHO
- ILLUSTRATIVE EXAMPLE 4.1
- ILLUSTRATIVE EXAMPLE 4.10
- ILLUSTRATIVE EXAMPLE 4.11
- ILLUSTRATIVE EXAMPLE 4.12
- ILLUSTRATIVE EXAMPLE 4.13
- ILLUSTRATIVE EXAMPLE 4.14
- ILLUSTRATIVE EXAMPLE 4.15
- ILLUSTRATIVE EXAMPLE 4.16
- ILLUSTRATIVE EXAMPLE 4.17
- ILLUSTRATIVE EXAMPLE 4.18
- ILLUSTRATIVE EXAMPLE 4.19
- ILLUSTRATIVE EXAMPLE 4.2
- ILLUSTRATIVE EXAMPLE 4.20
- ILLUSTRATIVE EXAMPLE 4.21
- ILLUSTRATIVE EXAMPLE 4.22
- ILLUSTRATIVE EXAMPLE 4.23
- ILLUSTRATIVE EXAMPLE 4.24
- ILLUSTRATIVE EXAMPLE 4.25
- ILLUSTRATIVE EXAMPLE 4.26
- ILLUSTRATIVE EXAMPLE 4.27
- ILLUSTRATIVE EXAMPLE 4.28
- ILLUSTRATIVE EXAMPLE 4.29
- ILLUSTRATIVE EXAMPLE 4.3
- ILLUSTRATIVE EXAMPLE 4.4
- ILLUSTRATIVE EXAMPLE 4.5
- ILLUSTRATIVE EXAMPLE 4.6
- ILLUSTRATIVE EXAMPLE 4.7
- ILLUSTRATIVE EXAMPLE 4.8
- ILLUSTRATIVE EXAMPLE 4.9