Illustrative Example 4.28 from GK PUBLICATIONS PHYSICS (HINGLISH) HEAT TRANSFER for Class 12

Class 12	PHYSICS
Chapter	HEAT TRANSFER
GK PUBLICATIONS PHYSICS (HINGLISH)	Illustrative Example 4.28
Medium	English
Academic Year	2023-2024

Question 1
Consider two rods of equal cross - sectionai area A, one of Aluminium and other of iron joined end to end as shown in figure -4.8. Length of the two rods and their thermal coductivities are $l_{1}, k_{1}$ and $l_{2}, k_{2}$ respectively . If the ends of the rods are maintained at temperature $T_{1}$ and $T_{2}, (T_{1} > T_{2})$ find the temperature of the junction in steady state .
View Solution
Question 2
A bar of copper of length 75 cm and a bar of steel of length 125 cm are joined together end to end . Both are of circular cross - section with diameter 2 cm . The free ends of the copper and steel bars are maintained at $100^{\circ} C$ and $0^{\circ} C$ respectively . The surface of the bars are thermally insulted . What is the temperature of the copper - steel junction ? What is the heat transmitted per unit time across the junction ? Thermal conductivty of copper $9.2 \times 10^{- 2} k c a l m^{- 1}$ $^{\circ} C^{- 1} s^{- 1}$ and that of steel is $1.1 \times 10^{- 2} k c a l m^{- 1} s^{- 1}$ $(\circ) C^{- 1}$ .View Solution
Question 3
A cylinderical brass boiler of radius 15 cm and thickness 1.0 cm is filled with water and placed on an elerctric heater. If the If the water boils at the rate of $200 g / s$ , estimate the temperature of the heater filament. Thermal conductivity of $b r a s s = 109 J / s / m^{\circ} C$ and heat of vapourization of water $= 2.256 \times 10^{3} J / g$ .View Solution
Question 4
A slab of stone of area of $0.36 m^{2}$ and thickness $0.1 m$ is exposed on the lower surface to steam at $100^{\circ} C$ . A block of ice at $0^{\circ} C$ rests on the upper surface of the slab. In one hour $4.8 k g$ of ice is melted. The thermal conductivity of slab is
(Given latent heat of fusion of ice $= 3.63 \times 10^{5} J k g^{- 1}$ )View Solution
Question 5
Few rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at $80^{\circ} C$ and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
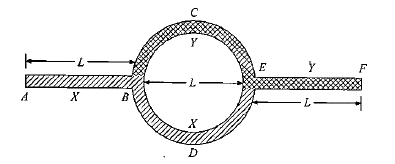View Solution
Question 6
The space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature $T_{1}$ and outer is maintained at a lower temperature $T_{2}$ . Calculate the rate of flow of heat in radially outward direction through the medium.View Solution
Question 7
A closed cubical box made of a perfectly insulating material has walls of thickness 8 cm and the only way for the heat to enter or leave the box is through two solid cylinderical metal plugs , each of cross - sectional area $12 c m^{2}$ and length 8 cm fixed in the opposite walls of the box . The outer surface A of one plug is kept at a temperature of $100^{\circ} C$ while the outer surface of the other plug is maintained at a temperature of $4^{\circ} C ~ . T h e t h e r m a l c o \in d u c t i v i t y o f t h e m a t e r i a l o f t h e p l u g i s$ 0.5 cal // cmsec""^(@)C $. A s o u r c e o f e \neq r g y \geq \neq r a t \in g$ 36 cal s^(-1) is enclosed inside the box . Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface
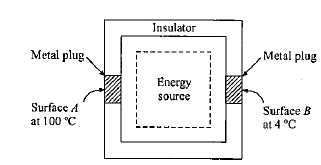View Solution
Question 8
Figure-4.13 shows a water tank at a constant temperature. $T_{0}$ and a small bodyof mass m, and specific heat S at a temperature $T_{1}$ . Given that $T_{1} < T_{0}$ . A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.
View Solution
Question 9
When two bodies ofmasses $m_{1}$ and $m_{2}$ with specific heats $s_{1}$ and $s_{2}$ at absolute temperatures $T_{10}$ and $T_{20} (T_{10} > T_{20})$ are connected by a rod of length l and cross sectional area A with thermal conductivity k. Find the temperature difference of the bodies after time t. Neglect any heat loss due to radiation at any surface..
View Solution
Question 10
Acubical container of side a and wall thickness x (a: « a) is suspendedin air and filled n molesof diatomic gas (adiabatic exponent=y) inaroom where room temperature isT^. Ifat/ = 0 gastemperature is Fj (F, > Fq), find the gas temperature as a function of time t. Assume the heat is conducted through all the walls ofcontainer.View Solution
Question 11
A layer of ice of $0^{\circ} C$ of thickness $x_{1}$ is floating on a pond. If the atmospheric temperature is $- 7^{\circ} C$ . Show that the time taken for thickness of the layer of ice to increase from $x_{1}$ to $x_{2}$ is given by
$t = \frac{p L}{2 k T} (x_{2}^{2} - x_{1}^{2})$
where p is the density of ice, k its thermal conductivity and L is the latent heat of fusion of ice. View Solution
Question 12
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at $60^{\circ} C$ and the junction E at $10^{\circ} C$ . Calculate the temperature of the junction B, C and D. The thermal conductivity of X is $0.92 c a l / sec - c m^{\circ} C$ and that of Y is $0.46 c a l / sec - c m -^{\circ} C$ .
View Solution
Question 13
An electric heater ofpower 1kW emits thermal radiations the surface area of heating element of heater is $200 c m^{2}$ . If this heating element is treated like a black bodyfind the temperature at its surface. Assume its temperature is very much higher then its surroundings.View Solution
Question 14
A cube of mass 1 kg and volume $125 c m^{2}$ is placed in an evacuated chamber at $27^{\circ} C$ . Initially temperature of block is $227^{\circ} C$ . Assume block behaves like a block body, find the rate of cooling of block if specific heat of the material of block is $400 J / k g - K$ .View Solution
Question 15
One end A of a metallic rod of length 10 cm is inserted in a furnace whose temperature is $827^{\circ} C$ . The curved surface of the rod is insulated. The room temperature is $27^{\circ} C$ . When the steady state is attained, the temperature of the other end B ofthe rod is $702^{\circ} C$ . Find the thermal conductivity ofthe metal. Stefan's constant $= 5.67 \times 10^{- 8} W m^{- 2} K^{- 4}$ .View Solution
Question 16
A solid metallic sphere of diameter 20 cm and mass 10 kg is heated to a temperature of $327^{\circ} C$ and suspended in a box in which a constant temperature of $27^{\circ} C$ is maintained. Find the rate at which the temperature of the Sphere will fall with time. Stefan's constant $= 5.67 \times 10^{- 8} W / m^{2} / K^{4}$ and specific heat of metal $= 420 J / k g /^{\circ} C$ .View Solution
Question 17
A cylindrical rod of 50 cm length and having $1 c m^{2}$ cross sectional area isused as a conducting material between an ice bath at $0^{\circ} C$ and a vacuum chamber at $27^{\circ} C$ as shown in figure. The end of rod which is inside the vacuum chamber behaves like a black body and is at temperature $17^{\circ} C$ in steady state. Find the thermal conductivity of the material of rod and rate at which ice is melting in the ice bath. Given that latent heat of fusion of ice is $3.35 \times l 0^{5} J / k g$ ..
View Solution
Question 18
The earth receives solar energy at the rate of 2 cal $C m^{- 2}$ per minute. Assuming theradiation tobeblack body in character, estimate the surface temperature of the sun. Given that $σ = 5.67 \times 10^{- 8} W m^{- 2} K^{- 4}$ and angular diameter of the sun =32 minute of arc.View Solution
Question 19
A spherical ball of radius 1cm coated with a metal having emissivity 0.3 is maintained at 1000 K temperature and suspended in a vacuum chamber whose walls are maintained at 300 K temperature. Find rate at which electrical energy is to be supplied to the ball to keep its temperature constant.View Solution
Question 20
There are two concentric spherical shells A and B of surface area $20 c m^{2}$ and $80 c m^{2}$ . Surfaces ofboth the shells behave like black bodies. It is given thatthethermal conductivity ofmaterial of B is very low and that of A is very high. Initially the temperature of 4 is 400 K and that of B is 300 k. Find the rate of change of temperature of A and B. Given that the heat capacities of A and B are $50 J /^{\circ} C$ and $80 J /^{\circ} C$ respectively. View Solution
Question 21
The temperature of a body in a surrounding of temperature $16^{\circ} C$ falls from $40^{\circ} C$ to $36^{\circ} C$ in 5 mins. Assume Newtons law of cooling to be valid and find the time taken by the body to reach temperature $32^{\circ} C$ .View Solution
Question 22
In a container some water is filled at temperature $50^{\circ} C$ .It cools to $45^{\circ} C$ in 5 minutes and to $40^{\circ} C$ in next 8 minutes. If we assume Newton's law of cooling to be valid in this case, find the surrounding temperature.View Solution
Question 23
A solid body X of heat capacity C is kept in an atmosphere whose temperature is $T_{A} = 300 K$ . At time $t = 0$ the temperature of X is $T_{0} = 400 K$ . It cools according to Newton's law of cooling. At time $t_{1}$ , its temperature is found to be 350K. At this time $(t_{1})$ , the body X is connected to a large box Y at atmospheric temperature is $T_{4}$ , through a conducting rod of length L, cross-sectional area A and thermal conductivity K. The heat capacity Y is so large that any variation in its temperature may be neglected. The cross-sectional area A of hte connecting rod is small compared to the surface area of X. Find the temperature of X at time $t = 3 t_{1} .$ View Solution
Question 24
A black walled metal container of negligible heat capacity is filled with water. The container has sides of length 10cm. It is placed in an evacuated chamber at $27^{\circ} C .$ How long will it take for the temperature of water to change from $30^{\circ} C \to 29^{\circ} C .$ View Solution
Question 25
A calorimeter of water equivalent 100gm cools in air in 18 minutes from $60^{\circ} C$ to $40^{\circ} C$ .When a block of metal of mass 60 gm is heated to $60^{\circ} C$ and placed inside the calorimeter. Assume heat loss only by radiation and Newton's Law of cooling to be valid. Find the specific heat of metal if now the system cools from $60^{\circ} C$ to $40^{\circ} C$ in 20 minutes.View Solution
Question 26
A metal ball of 1kg mass is heated by a 20W heater in a room at $20^{\circ} C$ . After some time temperature of ball becomes steady at $50'^{\circ} C$ . Find the rate of loss of heat by the ball to surrounding when its temperature becomes $50^{\circ} C$ . Also find the rate at which it looses heat to the surrounding when its temperature was $30^{\circ} C$ .View Solution
Question 27
A black body at 1500K emits maximum energy of wavlength 20000 $Å$ . If sun emits maximum energy of wavelength $5500 Å$ , what would be the temperature of sun.View Solution
Question 28
If the filament of a 100 W bulb has an area $0.25 c m^{2}$ and behaves as a perfect block body. Find the wavelength corresponding to the maximum in its energy distribution. Given that Stefan's constant is $σ = 5.67 \times 10^{- 8} J / m^{2} s K^{4}$ .View Solution
Question 29
A body emits maximum energy at 4253 $Å$ and the same body at some other temperature emits maximum energy at 2342 $Å$ . Find the ratio of the maximum energy radiated by the body in a short wavelength range.View Solution

All Exercises from GK PUBLICATIONS PHYSICS (HINGLISH) Class 12 PHYSICS HEAT TRANSFER

Home
Ask Doubt
Profile