Illustrative Example 4.22 from GK PUBLICATIONS PHYSICS (HINGLISH) HEAT TRANSFER for Class 12
| Class 12 | PHYSICS |
| Chapter | HEAT TRANSFER |
| GK PUBLICATIONS PHYSICS (HINGLISH) | Illustrative Example 4.22 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Consider two rods of equal cross - sectionai area A, one of Aluminium and other of iron joined end to end as shown in figure -4.8. Length of the two rods and their thermal coductivities are l1,k1and l2,k2 respectively . If the ends of the rods are maintained at temperature T1 and T2,(T1>T2) find the temperature of the junction in steady state .
 View Solution
View SolutionQuestion 2
A bar of copper of length 75 cm and a bar of steel of length 125 cm are joined together end to end . Both are of circular cross - section with diameter 2 cm . The free ends of the copper and steel bars are maintained at 100∘C and 0∘C respectively . The surface of the bars are thermally insulted . What is the temperature of the copper - steel junction ? What is the heat transmitted per unit time across the junction ? Thermal conductivty of copper 9.2×10−2kcalm−1∘C−1s−1 and that of steel is 1.1×10−2kcalm−1s−1(∘)C−1.View SolutionQuestion 3
A cylinderical brass boiler of radius 15 cm and thickness 1.0 cm is filled with water and placed on an elerctric heater. If the If the water boils at the rate of 200g/s, estimate the temperature of the heater filament. Thermal conductivity of brass=109J/s/m∘C and heat of vapourization of water =2.256×103J/g.View SolutionQuestion 4
A slab of stone of area of 0.36m2 and thickness 0.1m is exposed on the lower surface to steam at 100∘C. A block of ice at 0∘C rests on the upper surface of the slab. In one hour 4.8kg of ice is melted. The thermal conductivity of slab is
(Given latent heat of fusion of ice =3.63×105Jkg−1)View SolutionQuestion 5
Few rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
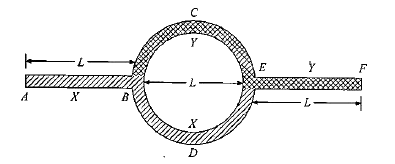 View Solution
View SolutionQuestion 6
The space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.View SolutionQuestion 7
A closed cubical box made of a perfectly insulating material has walls of thickness 8 cm and the only way for the heat to enter or leave the box is through two solid cylinderical metal plugs , each of cross - sectional area 12cm2 and length 8 cm fixed in the opposite walls of the box . The outer surface A of one plug is kept at a temperature of 100∘C while the outer surface of the other plug is maintained at a temperature of 4∘C~.Thethermalco∈ductivityofthematerialoftheplugis0.5 cal // cmsec""^(@)C.Asourceofe≠rgy≥≠rat∈g36 cal s^(-1) is enclosed inside the box . Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface
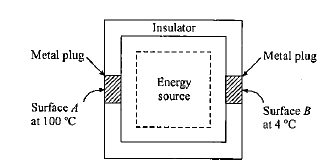 View Solution
View SolutionQuestion 8
Figure-4.13 shows a water tank at a constant temperature. T0 and a small bodyof mass m, and specific heat S at a temperature T1 . Given that T1<T0. A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.
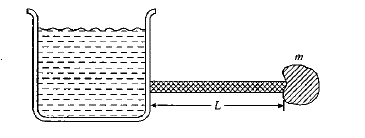 View Solution
View SolutionQuestion 9
When two bodies ofmasses m1 and m2 with specific heats s1 and s2 at absolute temperatures T10 and T20(T10>T20) are connected by a rod of length l and cross sectional area A with thermal conductivity k. Find the temperature difference of the bodies after time t. Neglect any heat loss due to radiation at any surface..
 View Solution
View SolutionQuestion 10
Acubical container of side a and wall thickness x (a: « a) is suspendedin air and filled n molesof diatomic gas (adiabatic exponent=y) inaroom where room temperature isT^. Ifat/ = 0 gastemperature is Fj (F, > Fq), find the gas temperature as a function of time t. Assume the heat is conducted through all the walls ofcontainer.View SolutionQuestion 11
A layer of ice of 0∘C of thickness x1 is floating on a pond. If the atmospheric temperature is −7∘C. Show that the time taken for thickness of the layer of ice to increase from x1 to x2 is given by
t=pL2kT(x22−x21)
where p is the density of ice, k its thermal conductivity and L is the latent heat of fusion of ice. View SolutionQuestion 12
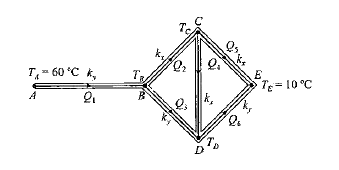
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
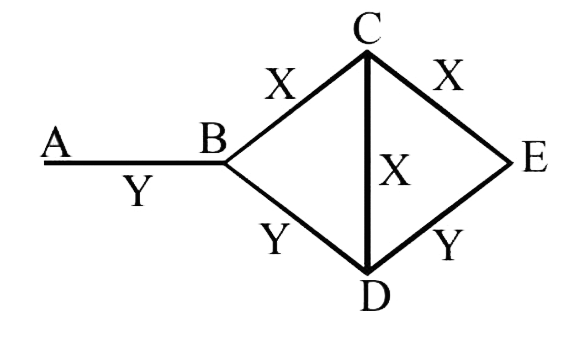 View Solution
View SolutionQuestion 15
One end A of a metallic rod of length 10 cm is inserted in a furnace whose temperature is 827∘C. The curved surface of the rod is insulated. The room temperature is 27∘C. When the steady state is attained, the temperature of the other end B ofthe rod is 702∘C. Find the thermal conductivity ofthe metal. Stefan's constant =5.67×10−8Wm−2K−4.View SolutionQuestion 16
A solid metallic sphere of diameter 20 cm and mass 10 kg is heated to a temperature of 327∘C and suspended in a box in which a constant temperature of 27∘C is maintained. Find the rate at which the temperature of the Sphere will fall with time. Stefan's constant=5.67×10−8W/m2/K4 and specific heat of metal =420J/kg/∘C.View SolutionQuestion 17
A cylindrical rod of 50 cm length and having 1cm2 cross sectional area isused as a conducting material between an ice bath at0∘C and a vacuum chamber at 27∘C as shown in figure. The end of rod which is inside the vacuum chamber behaves like a black body and is at temperature 17∘C in steady state. Find the thermal conductivity of the material of rod and rate at which ice is melting in the ice bath. Given that latent heat of fusion of ice is 3.35×l05J/kg..
 View Solution
View SolutionQuestion 19
A spherical ball of radius 1cm coated with a metal having emissivity 0.3 is maintained at 1000 K temperature and suspended in a vacuum chamber whose walls are maintained at 300 K temperature. Find rate at which electrical energy is to be supplied to the ball to keep its temperature constant.View SolutionQuestion 20
There are two concentric spherical shells A and B of surface area 20cm2 and 80cm2 . Surfaces ofboth the shells behave like black bodies. It is given thatthethermal conductivity ofmaterial of B is very low and that of A is very high. Initially the temperature of 4 is 400 K and that of B is 300 k. Find the rate of change of temperature of A and B. Given that the heat capacities of A and B are 50J/∘C and 80J/∘C respectively. View SolutionQuestion 23
A solid body X of heat capacity C is kept in an atmosphere whose temperature is TA=300K. At time t=0 the temperature of X is T0=400K. It cools according to Newton's law of cooling. At time t1, its temperature is found to be 350K. At this time (t1), the body X is connected to a large box Y at atmospheric temperature is T4, through a conducting rod of length L, cross-sectional area A and thermal conductivity K. The heat capacity Y is so large that any variation in its temperature may be neglected. The cross-sectional area A of hte connecting rod is small compared to the surface area of X. Find the temperature of X at time t=3t1.View SolutionQuestion 25
A calorimeter of water equivalent 100gm cools in air in 18 minutes from 60∘C to40∘C.When a block of metal of mass 60 gm is heated to 60∘C and placed inside the calorimeter. Assume heat loss only by radiation and Newton's Law of cooling to be valid. Find the specific heat of metal if now the system cools from 60∘C to 40∘C in 20 minutes.View SolutionQuestion 26
A metal ball of 1kg mass is heated by a 20W heater in a room at20∘C. After some time temperature of ball becomes steady at 50'∘C. Find the rate of loss of heat by the ball to surrounding when its temperature becomes 50∘C. Also find the rate at which it looses heat to the surrounding when its temperature was 30∘C.View Solution
All Exercises from GK PUBLICATIONS PHYSICS (HINGLISH) Class 12 PHYSICS HEAT TRANSFER
- PRACTICE EXERCISE 4.1
- PRACTICE EXERCISE 4.2
- PRACTICE EXERCISE 4.3
- PRACTICE EXERCISE 4.4
- DISCUSSION QUESTION
- CONCEPTUAL MCQS SINGLE OPTION CORRECT
- NUMERICAL MCQS SINGLE OPTIONS CORRECT
- ADVANCE MCQS WITH ONE OR MORE OPTION CORRECT
- UNSOLVED NUMERICAL PROBLEMS FOR PREPARATION OF NSEP,INPHO&IPHO
- ILLUSTRATIVE EXAMPLE 4.1
- ILLUSTRATIVE EXAMPLE 4.10
- ILLUSTRATIVE EXAMPLE 4.11
- ILLUSTRATIVE EXAMPLE 4.12
- ILLUSTRATIVE EXAMPLE 4.13
- ILLUSTRATIVE EXAMPLE 4.14
- ILLUSTRATIVE EXAMPLE 4.15
- ILLUSTRATIVE EXAMPLE 4.16
- ILLUSTRATIVE EXAMPLE 4.17
- ILLUSTRATIVE EXAMPLE 4.18
- ILLUSTRATIVE EXAMPLE 4.19
- ILLUSTRATIVE EXAMPLE 4.2
- ILLUSTRATIVE EXAMPLE 4.20
- ILLUSTRATIVE EXAMPLE 4.21
- ILLUSTRATIVE EXAMPLE 4.22
- ILLUSTRATIVE EXAMPLE 4.23
- ILLUSTRATIVE EXAMPLE 4.24
- ILLUSTRATIVE EXAMPLE 4.25
- ILLUSTRATIVE EXAMPLE 4.26
- ILLUSTRATIVE EXAMPLE 4.27
- ILLUSTRATIVE EXAMPLE 4.28
- ILLUSTRATIVE EXAMPLE 4.29
- ILLUSTRATIVE EXAMPLE 4.3
- ILLUSTRATIVE EXAMPLE 4.4
- ILLUSTRATIVE EXAMPLE 4.5
- ILLUSTRATIVE EXAMPLE 4.6
- ILLUSTRATIVE EXAMPLE 4.7
- ILLUSTRATIVE EXAMPLE 4.8
- ILLUSTRATIVE EXAMPLE 4.9