Motion Of Charged Particle In Magnetic Field from IE IRODOV PHYSICS Chapter 4 ELECTRODYNAMICS for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTRODYNAMICS |
| IE IRODOV PHYSICS | Motion Of Charged Particle In Magnetic Field |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
At the moment t=0 on electron leaves one plate of a parallel-plate capacitor with a neglible velocity. An accelerting volatage, varrying as V=at, where a=100V/s is applied between the plates is l=5.0cm. What is the velocity of the of the electron at the moment it reaches the opposite plate?View SolutionQuestion 2
A proton accelarted by a potential differnce V gets into the unifrom electric field of a paralallel-plate capacitor whose plates extended over a length l in the motion direction. The field strenth varies with time as E=at, where a is a constant. Assuming the proton to be non-relatistic, find the angle between the motion directions of the proton before and after its fight throgh the capacitor, the proton gets in the field at the moment t=0. The edge effects are to be neglected.View SolutionQuestion 3
A particle with specific charge q/m moves rectilinerarly due to an electric field E=E0−ax, where a is a positive constant, x is the distance from the point where the particle was initially at rest. Find:
(a) the distance covered by the particle till the moment it came to a standstill,
(b) the acceleration of the particle at that moment.View SolutionQuestion 6
At the moment t=0 a relativsitic proton files with a velocity v0 into the region where there is a unifrom transverse electric field of strength E, with v0⊥E. Find the time dependence of
(a) the angle θ between the proton's velocity vector v and the initial direction of its motion,
(b) the projection vx of the vector v on the initial direction of motion.View SolutionQuestion 7
A proton accelarted by a potential differnce V=500kV fieles through a unifrom transverse magnetic filed the induction B=0.54T. The field occupies a region of space d=10cm in thickness (Fig). Find the angle α through which the proton deviates from the initial direction of its motion.
View SolutionQuestion 12
A slightly divergent beam of non-relatistic charged particles accelearated by a potential difference V propagates from a point A along the axis of a straight solenoid. The beacm is brought into focus at a distance l from the point A at two successive values of magnetic induction B1 and B2. Find the spefic charge q/m of the particles.View SolutionQuestion 13
A non-relativistic electron originates at a point A lying on the axis of a striaght solenoid and moves with velocity v at an angle α to the axis. The magnetic induction of the field is equal to B. Find the distance r from the axis to the point on screen into which the electron strickes. The screeen into which the electron strikes. The screen is oriented at right angles to the axis and is located at a distance l from the point A.View SolutionQuestion 14
From the surface of a round wire of radius a carrying a direct current I an electron escapes with a velocity v0 perpendicular to the surface. Find what will be the maximum distance of the electron from the axis of the wire before it turns back due to the action of the magnetic field generated by the current.View SolutionQuestion 15
A non-relativistic charged particle files through the electric field of a cyclindrical capacitor and gets into a unifrom transverse magnetic field with induction B(fig). In the capacitor the particle moves along the are of a circle, in the magnetic field, along a semi-circle of radius r. The potential differnce applied to the capacitor is equal to V, the radii of the electrodes are equal to a and b, with a<b. Find the velocity of the particle and its specific charge q/m.
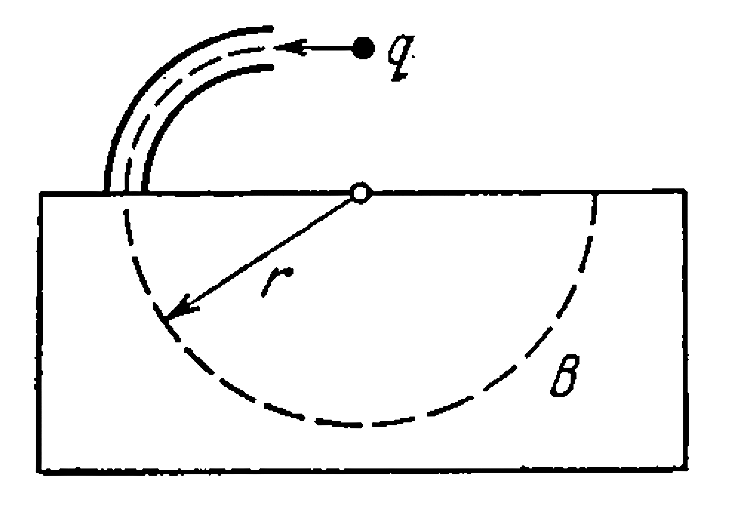View SolutionQuestion 16
Unifrom electric and magnetic fields with strength E and induction B respectively are directed along the y axis (Fig). A particle with specific charge q/m leaves the origin O in the direction of the z axis with an initial non-realtive velocity v0 find:
(a) the coordinate yn of the particle when it crossses then y axis for the nth time,
(b) the angle α between the particle's velocity vector and the y axis at that moment.
View SolutionQuestion 17
A narrow beam of identical ions with specific charge q/m, possessing different velocities, enters the region of space, where there are unifrom parallel electric and marnetic fields the strength E and induction B, at the point O (see Fig). The beam direction coincides with the x axis at the point O. A plane screen oriented at right angles to the x axis is located at a distance l from the point O. Find the equation of the trace that the ions leave on the screen. Demonstrate that at x<<l it is the equaction of a parabola.
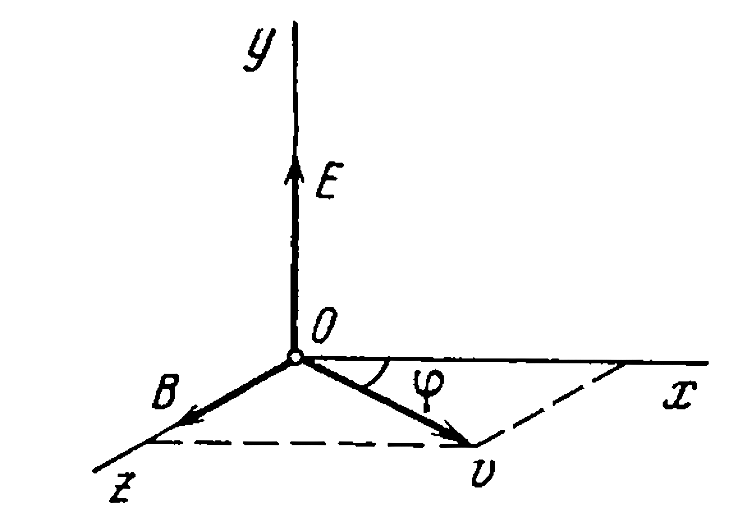View SolutionQuestion 18
A non-relativistic protons beam passes without diviation through the region of space where there are unifrom transverse mutually perpendicular electric and magnetic fields with E=120kV/m and B=50mT. Then the beam strikes a grounded target. Find the force with which the beam acts on the target if the beam current is equal to I=0.80mA.View SolutionQuestion 19
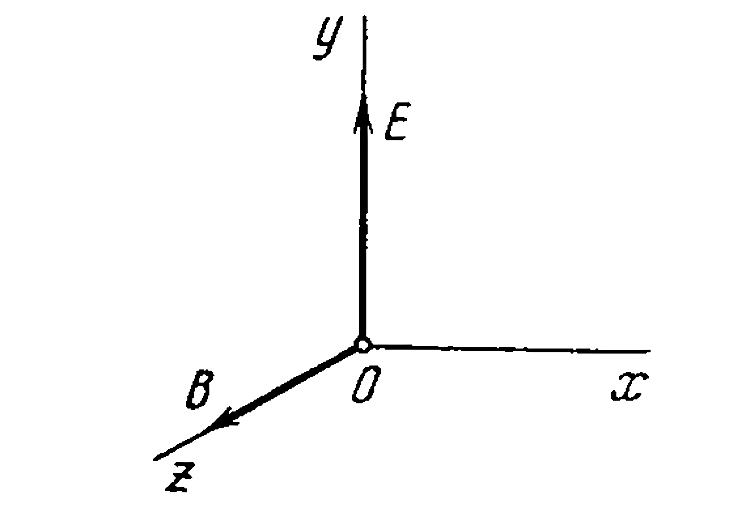
Non-relativistic protons move rectinearly in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with E=4.0kV/m and B=50mT. The trajectory of the protons lies in the plates xz (Fig) and forms an angle φ=30∘ with the x axis. Find teh pithc of the helical trajectory along which the protons will move after the electric field is swiched off.View SolutionQuestion 20
A beam of non-relatitivistic chagred particles moves without deviation through the region of space A (fig) where there are transerve mutually perpendicular electric and magnetic fields with streght E and induction B. When the magnetic field is swichted off, the trace of the beam on the screen S shifts by Δπ. Knowing the distances a and b, find the spefic charge q/m of the particles.
View SolutionQuestion 21
A particle with specific charge q/m moves in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with strength E and induction B (fig). At the moment t=0 the particle was located at the point O and had zero velocity. For the non-relativistic case find:
(a) the law of motion x(f) and y(t) of the particle, the shape of the trajectory,
(b) the lenght of the segment of the trajectory between two nearest points at which the velocity of the particle turns into zero,
(c) the mean value of the particle's velocity vector projections on the x axis (the drift velocity).
View SolutionQuestion 22
A sytem consists of a long cylindrical anode of radius a and a coxial cylindrical cylindrical cathode of radius b(b<a). A filament located along the axis of the system carries a heating current I producing a magnetic field in the surrounding space. FInd the least potentilal differnce between the cathode and anode at which the therimal electrons leaving the cathode without intital velcity start reaching the anode.View SolutionQuestion 23
Magentron is a device consisting of a filament of radius a and coaxial cylindrical anode of radius b which are located in a unifrom magnetic field parallel to the filament. An accelerating potential differnece V is applied between the filament and the anode. Find the value of magnetic induction at which the electrons leaving the filamnent with zero velocity reach the anode.View SolutionQuestion 24
A charged particle with specfic charge q/m starts moving in the region of space where there are unifrom mutually perpendicular electric and magnitude fields. The magentic field is constant and has an induction B while the strength of the electric field varies with time as E=Emcosωt, where ω=qB/m. For the non-relativistic case find the law of motion x(t) and y(t) of the particle if at the moment t=0 it was located at the point O (see Fig). What is the appoximate shape of the trajectory of the particle?
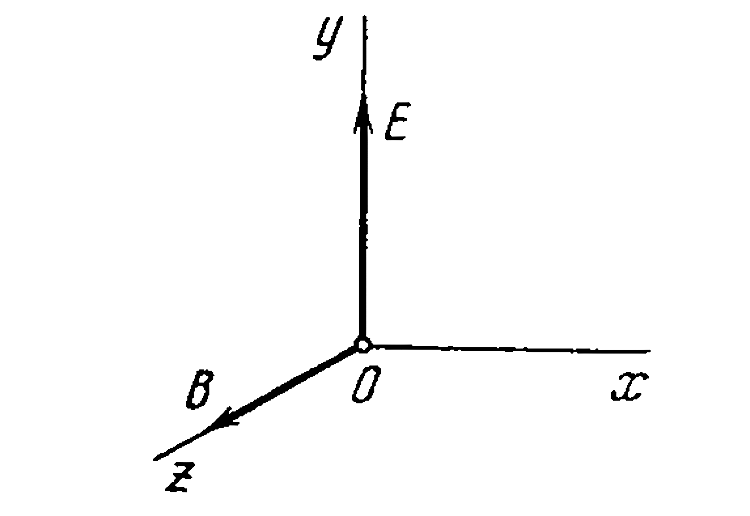View SolutionQuestion 26
Protons are accelerated in a cyclotron so that the maximum curvature radius of their trajectory is equal to r=50cm. Find:
(a) the kinetic energy of the protons when the acceleration is completed if the magnetic induction in the cyclotron is B=1.0T,
(b) the minimum frequency of the cycloroton's oscillator at which the kinetic energy of the protons amounts to T=20MeV by the end of accelearation.View SolutionQuestion 27
Singly charged ions He+ are accelerated in a cyclotron so that their maximum orbital radiys is r=60cm. The frequency of a cyclotron's oscillator is equal to v=10.0MHz, the effective accelearating volatage across the deos is V=50kV. Neglecting the gap between the does, find:
(a) the total time of acceleration of the ion,
(b) the appoximate distance covered by the ion in the process of its acceleration.View SolutionQuestion 28
since the period fo revolution of electrons in a unifrom magnetic field rapidly increases with the growth of energy, a cyclotron in unsuitable for their accelearation. This drawback is rectified in a microton (Fig) in which a change ΔT in the period of revolution of an electron is made multipile with the period of acclerating field T0. How many times has an electron to cross the accerating gap of a microtron to acquire an energy W=4.6MeV if ΔT=T0 the magnetic induction is equal to B=107mT, and the frequency of accelerating field to v=3000MHz ?
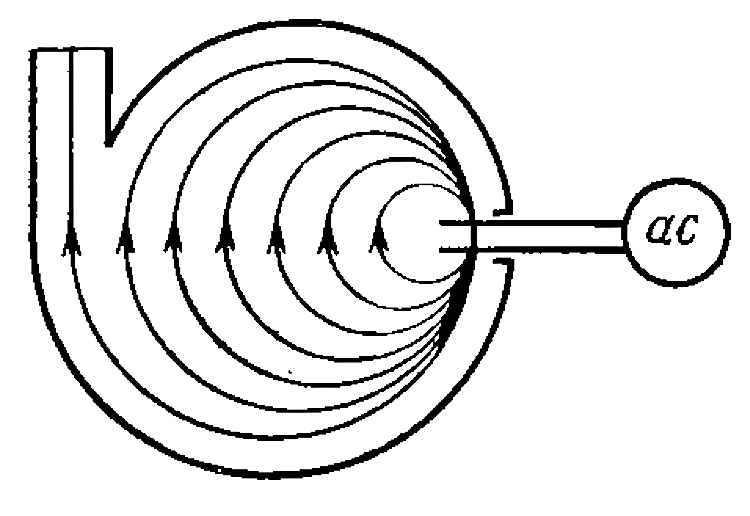View SolutionQuestion 29
The ill effects associated with the variatiion of the period of revolution of the particle in a cyclotron due to the increase of its energy are eleminated by slow monitoring (modulating ) the frequency of accelerting field. According to what law ω(t) should this frequencecy by mointored if the masgnetic induction is equal to B and the particle acquires an energy ΔW per revolution ? The charge of the particle is q and its mass is m.View SolutionQuestion 30
A particle with specific charge q/m is located inside a round solenoid at a distance r from its axis. With the current swichted into the winding, the magnetic induction of the field generated by the solenoid amounts to B. Find the velocity of the particle and the curvature radius of its trajectory,n assuming that during the increase of current flowing in the solenoid the particle shifts by a negligible distance.View SolutionQuestion 31
In a betatron the magnetic flux across an equilibrium orbit of radius r=25cm grows during the acceleration time at paractically constant rate Φ=5.0Wb/s. In the process, the electrons acquire an energy W=25MeV. Find the number of revolutions made by the electron during the acedeleration time and the corresponding distance covered by it.View SolutionQuestion 32
Demonstarate that electrons move in a betatron along a round orbit of constant radius provided the magnetic induction on the orbit of constant radius provided the magnetic induction on the orbit is equal to half the mean value of that indide the orbit (the betatron condition).View SolutionQuestion 36
The magnetic induction in betatron on an equlibrium orbit of radius r varies during the acceleration time at paractically constant rate from zero to B. Assuming the initial velocity of the electron to be equal to zero, find:
(a) the energy acquired by the electron during the acceleration time,
(b) the corresponding distance covered by the electron if the accelearation time is equal to Δt.View Solution