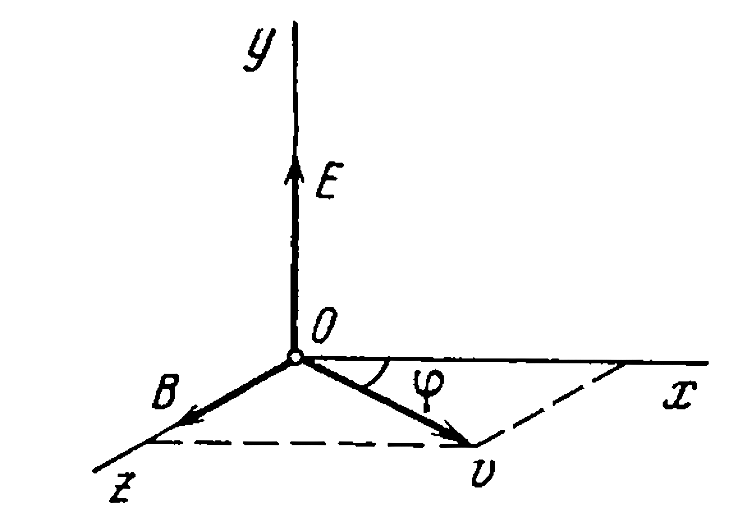
A narrow beam of identical ions with specific charge , possessing different velocities, enters the region of space, where there are unifrom parallel electric and marnetic fields the strength and induction , at the point (see Fig). The beam direction coincides with the axis at the point . A plane screen oriented at right angles to the axis is located at a distance from the point . Find the equation of the trace that the ions leave on the screen. Demonstrate that at it is the equaction of a parabola.
The equcation of the trajectory is,
as before see (3.384)
Now on the screen , so
or,
At that moment,
so,
and
For small
or, is a parabola.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y

View SolutionFind the electric field potentail and strength at the centre of a hemisphere fo raidus R ahcged uniformly with the the surface density σ.
View SolutionCurrents l1andI2 flow in the same direction along two parallel conductors, with l1>l2 • In which of the three regions I,IIorIII, and at what distance from the conductor carryi ng current 11 is the magnetic induction equal to zero?
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30^@ with x-axis . Then
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V . It moves through the electric field and exists at point B . The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged. . Find electric field.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
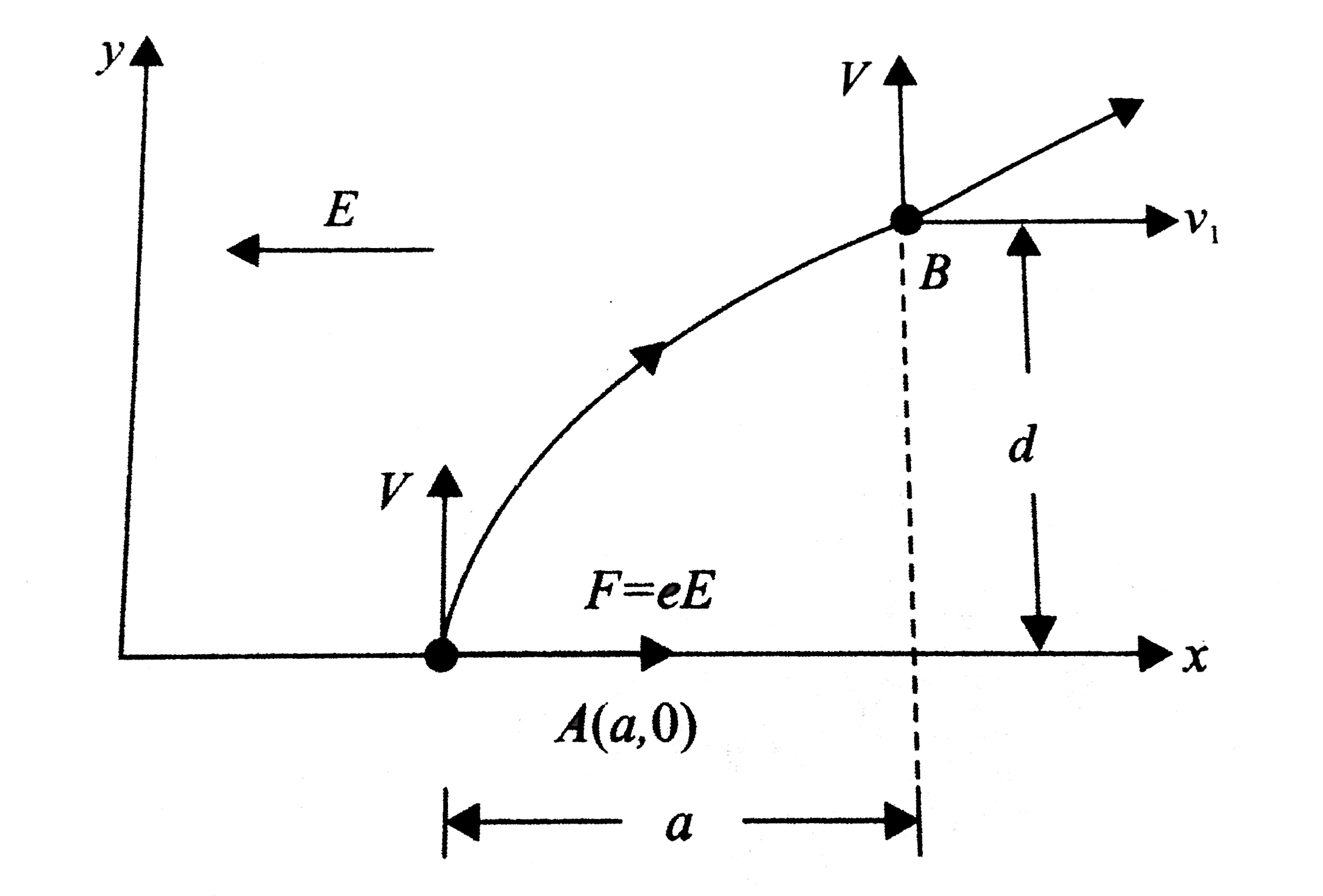 .
.
Find velocity at B.
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate y_nofthepartic≤whenitcrossesthey−aξsforthen^(th) time is
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q//m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v_0 The angle alpha between the particle's velocity vector and y-axis at and moment is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point 2a, b//2 , 0 its speed becomes 2v. Find the value of electric field strength of m, v and co-ordinates.
View SolutionA non-relativistic protons beam passes without diviation through the region of space where there are unifrom transverse mutually perpendicular electric and magnetic fields with E = 120 kV//m and B = 50 mT . Then the beam strikes a grounded target. Find the force with which the beam acts on the target if the beam current is equal to I = 0.80mA .
View SolutionA charged particle with specfic charge q//m starts moving in the region of space where there are unifrom mutually perpendicular electric and magnitude fields. The magentic field is constant and has an induction B while the strength of the electric field varies with time as E = E_(m) cos omega t , where omega = qB//m . For the non-relativistic case find the law of motion x(t) and y(t) of the particle if at the moment t = 0 it was located at the point O (see Fig). What is the appoximate shape of the trajectory of the particle?
View SolutionA narrow beam of identical ions with specific charge q/m, possessing different velocities, enters the region of space, where there are uniform parallel electric and magnetic fields with strengths E and B , at the point O. The beam direction coincides with the x-axis at the point O. A plane screen oriented at right angles to the x-axis is located at a distance I from O. Find the equation of trace that the ion leaves on the screen. Demonostrate that at z lt lt l , it is the equation of a parabola.
View SolutionA beam of non-relativistic charged particles moves without deviation through the region of space A where there are transverse mutually perpendicular electric and magnetic fields with strength E and induction B. When the magnetic field is switched off, the trace of the beam on the screen S shifts by Δx. Knowing the distance a and b, find the specific charge q/m of the particles.
View SolutionA uniform electric field of strength e exists in a region. An electron (charge -e, mass m) enters a point A with velocity V hat(j) . It moves through the electric field & exits at point B. Then :
View SolutionA uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is 2v at 30^@ with x-axis . Then
View Solution
