PROBLEMS from RESNICK AND HALLIDAY PHYSICS Chapter 30 RIGID BODY DYNAMICS - I for Class 12
| Class 12 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS - I |
| RESNICK AND HALLIDAY PHYSICS | PROBLEMS |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 76 cm and for rotation less than 1 rev, what are the (a) smallest and (b) largest angular speeds that cause the toast to hit and then topple to be butter-side down?View SolutionQuestion 4
The angular position of a point on a rotating wheel is given by θ=2.0+4.0t2+2.0t3, where θ is in radians and t is in seconds. At t = 0, what are (a) the point's angular position and (b) its angular velocity? ( c) What is its angular velocity at t = 3.0 s? (d) Calculate its angular acceleration at t = 4.0 s. (e) Is its angular acceleration constant?View SolutionQuestion 6
The wheel in figure has eight equally spaced spokes and of 30cm. It is mounted on a fixed axle and is spinning at 2.5rev/s. You want to shoot a 20−cm−long arrow parallel to this axle and through the wheel without hitting any of the spokes. Assume that the arrow and the spokes are very thin. What minimum speed must the arrow have ?
 .View Solution
.View SolutionQuestion 7
The angular acceleration of a wheel is α=6.0t4−4.0t2, with α in radians per second-squared and t in seconds. At time t = 0, the wheel has an angular velocity of +2.5 rad/s and an angular position of +1.5 rad. Write expressions for (a) the angular velocity (rad/s) and (b) the angular position (rad) as functions of time (s).View SolutionQuestion 9
Starting from rest, a disk rotates about its central axis with constant angular acceleration. In 5.0 s, it rotates 20 rad. During that time, what are the magnitudes of (a) the angular acceleration and (b) the average angular velocity? ( c) What is the instantaneous angular velocity of the disk at the end of the 5.0 s? (d) With the angular acceleration unchanged, through what additional angle will the disk turn during the next 5.0 s?View SolutionQuestion 10
Two identical disks A and B can spin around vertical axes. Disk A is spinning with an initial angular speed of 40 rev/s when its rim touches initially stationary disk B, causing that disk to begin to spin. The rubbing at the contact point slows A while speeding up B. The rate at which both disks change their angular speeds is 2.0rev/s2. Find the time required for the two disks to reach the same angular speed.View SolutionQuestion 12
A flywheel turns through 40 rev as it slows from an angular speed of 1.5 rad/s to a stop. (a) Assuming a constant angular acceleration, find the time for it to come to rest. (b) What is its angular acceleration? ( c) How much time is required for it to complete the first 20 of the 40 revolutions?View SolutionQuestion 13
A disc rotates about the central axis starting from rest and accelerates with constant angular acceleration. At one time, it is rotating at 10rps , 60 revolution later, its angular speed is 15rps. Calculate (i) angular acceleration (ii) time required to complete 60 revolutions (iii) the time required to reach 10rev/sec angular speed and (iv) number of revolutions from rest until the time the disc reaches 10rps angular speed.View SolutionQuestion 15
At t = 0, a flywheel has an angular velocity of 4.7 rad/s, a constant angular acceleration of −0.25rad/s2, and a reference line at θ0=0 (a) Through what maximum angle θmax will the reference line turn in the positive direction? What are the (b) first and ( c) second times the reference line will be at θ=1/2θmax? At what (d) negative time and (e ) positive time will the reference line be at θ = 10.5 rad ? (f) Graph θ versus t, and indicate your answers.View SolutionQuestion 16
An open jar of water moves in a vertical circle of radius 0.50 m with a frequency that is small enough to put the water on the verge of falling out of the jar at the top of the circle. If the same demonstration is only 3.7m/s2, what is the change in the circling frequency to again put the water on the verge of falling out at the top point?View SolutionQuestion 17
An object rotates about a fixed axis, and the angular position of a reference line on the object is given by θ=0.40e2t, where θ is in radians and t is in seconds. Consider a point on the object that is 6.0 cm from the axis of rotation. At t = 0, what are the magnitudes of the point's (a) tangential component of acceleration and (b) radial component of acceleration?View SolutionQuestion 19
Starting from rest at time t = 0, a circus stunt man drives a motorbike on a horizontal circular track of radius 10.0 m. His speed is given by v=ct2, where c=1.00m/s3. At t = 2.00 s, what is the angle between his (total) acceleration vector and his radial acceleration vector?View SolutionQuestion 20
A flywheel with a diameter of 1.20 m is rotating at an angular speed of 200 rev/min. (a) What is the angular speed of the flywheel in radians per second? (b) What is the linear speed of a point on the rim of the flywheel? ( c) What constant angular acceleration (in revolutions per minute-squared) will increase the wheel's angular speed to 1000 rev/min in 60.0 s? (d) How many revolutions does the wheel make during that 60.0 s?View SolutionQuestion 22
The flywheel of a steam engine runs with a constant angular velocity of 160 rev/min. When steam is shut off, the friction of the bearings and of the air stops the wheel in 2.2 h. (a) What is the constant angular acceleration, in revolutions per minute-squared, of the wheel during the slowdown? (b) How many revolutions does the wheel make before stopping? ( c) At the instant the flywheel is turning at 75 rev/min, what is the tangential component of the linear acceleration of a flywheel particle that is 50 cm from the axis of rotation? (d) What is the magnitude of the net linear acceleration of the particle in ( c) ?View SolutionQuestion 23
A seed is on a turntable rotating at 331/3 rev/min, 6.0 cm from the rotation axis. What are (a) the seed's acceleration and (b) the least coefficient of static friction to avoid slippage? ( c) If the turntable has undergone constant angular acceleration from rest in 0.25 s, what is the least coefficient to avoid slippage?View SolutionQuestion 24
In Fig. 10-54, wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 2.0rad/s2. Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip.
 View Solution
View SolutionQuestion 25
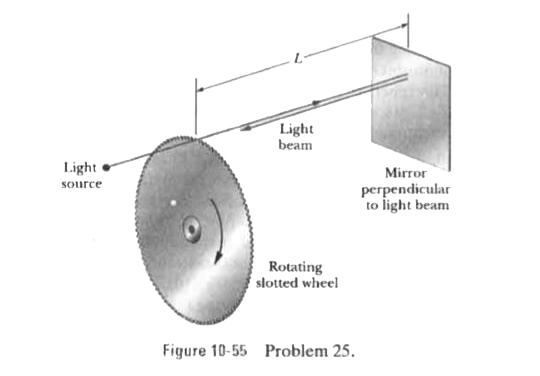
Figure 10-55 shows an early method of measuring the speed of light that makes use of a rotating slotted wheel. A beam of light passes through one of the slots at the outside edge of the wheel, travels to a distant mirror, and returns to the wheel just in time to pass through the next slot in the wheel. One such slotted wheel has a radius of 5.0 cm and 500 slots around its edge. Measurements taken when the mirror is L = 500 m from the wheel indicate a speed of light of 3.0×105km/s. (a) What is the (constant) angular speed of the wheel? (b) What is the linear speed of a point on the edge of the wheel?
 View Solution
View SolutionQuestion 26
A disk, with a radius of 0.25 m, is to be rotated like a merry-go-round through 800 rad, starting from rest, gaining angular speed at the constant rate α1 through the first 400 rad and then losing angular speed at the constant rate - α1 until it is again at rest. The magnitude of the centripetal acceleration of any portion of the disk is not to exceed 400m/s2. (a) What is the least time required for the rotation? (b) What is the corresponding value of α1?View SolutionQuestion 27
A car starts from rest and moves around a circular track of radius 32.0 m. Its speed increases at the constant rate of 0.600m/s2. (a) What is the magnitude of its net linear acceleration 15.0 s later? (b) What angle does this net acceleration vector make with the car's velocity at this time?View SolutionQuestion 28
(a) A uniform 2.00 kg disk of radius 0.300 m can rotate around its central axis like a merry-go-round. Beginning from rest at time t = 0, it undergoes a constant angular acceleration of 30.0rad/s2. When is the rotational kinetic energy equal to 2000 J? (b) Repeat the calculation but substitute a ring of the same mass and radius and assume that the spokes have negligible mass.View SolutionQuestion 29
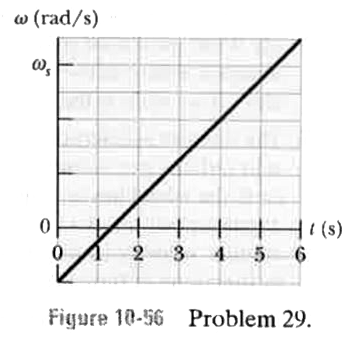
Figure 10-56 gives angular speed versus time for a thin rod that rotates around one end. The scale on the ω axis is set by ωs=60rad/s. (a) What is the magnitude of the rod's angular acceleration? (b) At t = 4.0 s, the rod has a rotational kinetic energy of 1.60 J. What is its kinetic energy at t = 0?
 View Solution
View SolutionQuestion 30
A meter stick of negligible mass can rotate about a vertical axis through a point at distant x from the point marked "0". A small block of mass 0.100 kg is glued at the mark of "0" and a small block of mass 0.500 kg is glued at the opposite end, at the mark of "1." The stick and blocks are to rotate with an angular speed of 5.00 rad/min. (a) For what choice of x is the associated rotational kinetic energy least and (b) what is that least erergy?View SolutionQuestion 31
Figure 10-57 a shows a disk that can rotate about an axis at a radial distance h from the center of the disk. Figure 10-57b gives the rotational inertia I of the disk about the axis as a function of that distance h, from the center out to the edge of the disk. The scale on the I axis is set by IA=0.050kg⋅m2andIB=0.150kg⋅m2. What is the mass of the disk?
 View Solution
View SolutionQuestion 33
Figure 10-58 shows three 0.0100 kg particles that have been glued to a rod of length L = 8.00 cm and negligible mass. The assembly can rotate around a perpendicular axis through point O at the left end. If we remove one particle (that is, 33% of the mass), by what percentage does the rotational inertia of the assembly around the rotation axis decrease when that removed particle is (a) the inner-most one and (b) the outermost one?
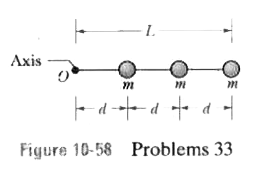 View Solution
View SolutionQuestion 34
A wheel with a rotational inertia of 0.50kg⋅m2 about its central axis is initially rotating at an angular speed of 15 rad/s. At time t = 0, a man begins to slow it at a uniform rate until it stops at t = 5.0 s. (a) By time t = 3.0 s, how much work had the man done? (b) For the full 5.0 s, at what average rate did the man do work?View SolutionQuestion 35
Figure 10-59 shows an arrangement of 15 identical disks that have been glued together in a rod-like shape of length L = 1.0000 m and (total) mass M = 100.0 mg. The disks are uniform, and the disk arrangement can rotate about a perpendicular axis through its central disk at point O. (a) What is the rotational inertia of the arrangement about that axis? (b) If we approximated the arrangement as being a uniform rod of mass M and length L, what percentage error would we make in using the formula in Table 10-2e to calculate the rotational inertia?
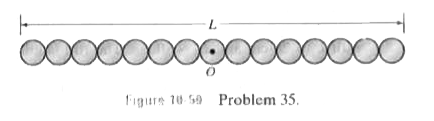 View Solution
View SolutionQuestion 36
In Fig. 10-60, two particles, each with mass m = 0.85 kg, are fastened to each other, and to a rotation axis at O, by two thin rods, each with length d = 5.6 cm and mass M = 1.2 kg. The combination rotates around the rotation axis with the angular speed ω=0.30rad/s. Measured about O, what are the combination's (a) rotational inertia and (b) kinetic energy?
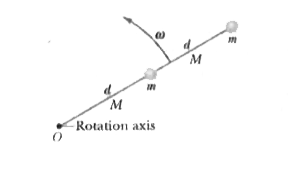 View Solution
View SolutionQuestion 37
Figure 10-61 is an overhead view of a rod of length 1.0 m and mass 1.0 kg that is lying stationary on a frictionless surface when three bullets hit it simultaneously. The bullets move along paths that are in the plane of the rod and per-pendicular to the rod. Bullet 1 has mass 10 g and speed 2.0 m/s. Bullet 2 has mass 20 g and speed 3.0 m/s. Bullet 3 has mass 30 g and speed 5.0 m/s. The labelled distance are α=10cm, b = 60 cm, and c = 80 cm. As a result of the impacts, the rod-bullets system rotates around its center of mass while the center of mass moves in a straight line over the frictionless surface. (a) What is the linear speed of the system's center of mass? (b) What is the distance between the rod's center and the system's center of mass ? ( c) What is the rotational inertia of the system about the system's center of mass?
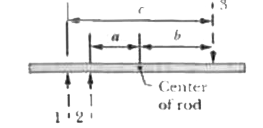 View Solution
View SolutionQuestion 39
Four identical particles of mass 0.75 kg each are placed at the vertices of a 2.0m×2.0m square and held there by four massless rods, which form the sides of the square. What is the rotational inertia of this rigid body about an axis that (a) passes through the midpoints of opposite sides and lies in the plane of the square, (b) passes through the midpoint of one of the sides and is perpendicular to the plane of the square, and ( c) lies in the plane of the square and passes through two diagonally opposite particles?View SolutionQuestion 41
A 60 kg father and 20 kg child sit on opposite ends of a seesaw consisting of a board of length 4.0 m and negligible mass. The pivot can be placed anywhere between the father and the child. At what distance from the child should it be placed so that the seesaw is balanced when the father and child are stationary?View SolutionQuestion 43
A cord with negligible mass is wrapped around a pulley that is a uniform disk of mass 5.00 kg and radius 0.300 m and that can rotate without friction about its central axis. A 1.0 kg bucket is attached at the free end of the cord hanging down from the pulley and then released at time t = 0. The cord begins to unwrap from the pulley as the bucket descends. At t = 5.00 s, through how many rotations has the pulley turned (the bucket is still descending)?View SolutionQuestion 45
In Fig. 10-64, block 1 has mass m1=460g, block 2 has mass m2=500g, and the pulley, which is mounted on a horizontal axle with negligible friction, has radius R = 5.00 cm. When released from rest, block 2 falls 75.0 cm in 5.00 s without the cord slipping on the pulley. (a) What is the magnitude of the acceleration of the blocks? What are (b) tension T2 and ( c) tension T1? (d) What is the magnitude of the pulley's angular acceleration? (e) What is its rotational inertia?
 View Solution
View SolutionQuestion 46
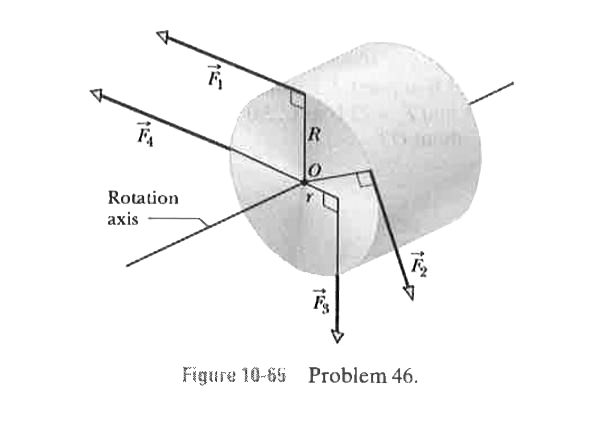
In Fig. 10-65, a cylinder having a mass of 3.0 kg can rotate about its central axis through point O. Forces are applied as shown: F1=6.0N,F2=4.0N,F3=2.0NandF4=5.0N. Also, r = 5.0 cm and R = 12 cm. Find the (a) magnitude and (b) direction of the angular acceleration of the cylinder. (During the rotation, the forces maintain their same angles relative to the cylinder.)
 View Solution
View SolutionQuestion 47
Figure shows a uniform disk that can rotate around its center like a merry-go-round. The disk has a radius of 2.00 cm and a mass of 20.0 grams and is initially at rest. Starting at time t = 0, two forces are to be applied tangentially to the rim as indicated, so that at time t = 1.25 s the disk has an angular velocity of 250 rad/s counterclockwise. Force →F1 has a magnitude of 0.100 N. What is magnitude F2 ?
 View Solution
View SolutionQuestion 48
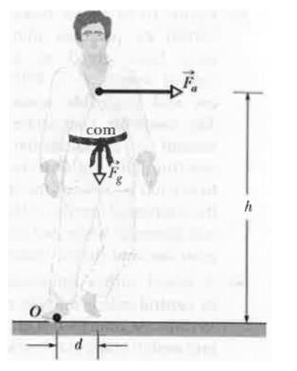
In a judo foot-sweep move, you sweep your opponent's left foot out from under him while pulling on his gi (uniform) toward that side. As a result, your opponent rotates around his right foot and onto the mat. Figure 10-67 shows a simplified diagram of your opponent as you face him, with his left foot swept out. The rotational axis is through point O. The gravitational force →Fg on him effectively acts at his center of mass, which is a horizontal distance d = 28 cm from point O. His mass is 75 kg, and his rotational inertia about point O is 65kgm2. What is the magnitude of his initial angular acceleration about point O if your pull →Fa on his gi is (a) negligible and (b) horizontal with a magnitude of 300 N and applied at height h = 1.4 m?
 View Solution
View SolutionQuestion 49
Figure shows particles 1 and 2, each of mass m, fixed to the ends of a rigid massless rod of length L1+L2,with L1=20cmandL2=80cm. The rod is held horizontally on the fulcrum and then released. What are the magnitudes of the initial accelerations of (a) particle 1 and (b) particle 2?
 View Solution
View SolutionQuestion 50
A pulley, with a rotational inertia of 1.0×10−3kg⋅m2 about its axle and a radius of 10 cm, is acted on by a force applied tangentially at its rim. The force magnitude varies in time as F=0.50t+0.30t2, with F in newtons and t in seconds. The pulley is initially at rest. At t = 3.0 s what are its (a) angular acceleration and (b) angular speed?View SolutionQuestion 53
A thin rod of length 0.75 m and mass 0.42 kg is suspended freely from one end. It is pulled to one side and then allowed to swing like a pendulum, passing through its lowest position with angular speed 3.5 rad/s. Neglecting friction and air resistance, find (a) the rod's kinetic energy at its lowest position and (b) how far above that position the center of mass rises.View SolutionQuestion 55
A uniform cylinder of radius 12 cm and mass 25 kg is mounted so as to rotate freely about a horizontal axis that is parallel to and 5.0 cm from the central longitudinal axis of the cylinder. (a) What is the rotational inertia of the cylinder about the axis of rotation? (b) If the cyliner is released from rest with its central longitudinal axis at the same height as the axis about which the cylinder rotates, what is the angular speed of the cylinder as it passes through its lowest position?View SolutionQuestion 56
A tall, cylindrical chimney falls over when its base is ruptured. Treat the chimney as a thin rod of length 55.0 m. At the instant it makes an angle of 35.0∘ with the vertical as it falls, what are (a) the radial acceleration of the top, and (b) the tangential acceleration of the top. ( c) At what angle θ is the tangential acceleration equal to g?View SolutionQuestion 57
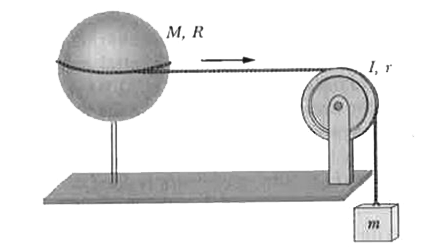
A uniform spherical shell of mass M = 4.5 kg and radius R = 8.5 cm can rotate about a vertical axis on frictionless bearings (Fig. 10-69). A massless cord passes around the equator of the shell, over a pulley of rotational inertia I=3.0×10−3kg⋅m2 and radius r = 5.0 cm, and is attached to a small object of mass m = 0.60 kg. There is no friction on the pulley's axle, the cord does not slip on the pulley. What is the speed of the object when it has fallen 82 cm after being released from rest? Use energy considerations.
 View Solution
View SolutionQuestion 58
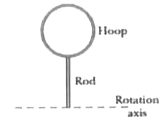
Figure shows a rigid assembly of a thin hoop (of mass m and radius R = 0.150 m) and a thin radial rod (of mass m and length L = 2.00R). The assembly is upright, but if we give it a slight nudge, it will rotate around a horizontal axis in the plane of the rod and hoop, through the lower end of the rod. Assuming that the energy given to the assembly in such a nudge is negligible, what would be the assembly's angular speed about the rotation axis when it passes through the upside-down (inverted) orientation?
 View Solution
View SolutionQuestion 62
A particle moves through an xyz coordinate system while a force acts on the particle. When the particle has the position vector →r=(2.00m)ˆi−(3.00m)ˆj+(2.00m)ˆk, the force is given by →F=Fxˆi+(7.00N)ˆj−(6.00N)ˆk and the corresponding torque about the origin is →τ=(400N⋅m)ˆi+(2.00N⋅m)ˆj−(1.00N⋅m)ˆk. Determine Fx.View SolutionQuestion 65
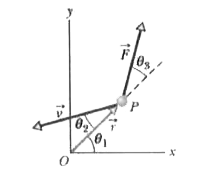
At the instant of Figure, a 2.0 kg particle P has a position vector →r of magnitude 5.0 m and angle θ1=45∘ and a velocity vector →v of magnitude 4.0 m/s and angle θ2=30∘, Force →F, of magnitude 2.0 N and angle θ3=30∘, acts on P. All three vectors lie in the xy plane. About the origin, what are the (a) magnitude and (b) direction of the angular momentum of P and the ( c) magnitude and (d) direction of the torque acting on P?
 View Solution
View SolutionQuestion 66
A particle of mass m is shot from ground level at initial speed u and initial angle θ relative to the horizontal. When it reaches its highest point in its flight over the level ground, what are the magnitudes of (a) the torque acting on it from the gravitational force and (b) its angular momentum, both measured about the launch point?View SolutionQuestion 67
A 3.0 kg particle-like object moves in a plane with velocity components vx=30m/sandvy=60m/s as is passes through the point with (x, y) coordinates of (3.0, -4.0) m. Just then, in unit vector notation, what is its angular momentum relative to (a) the origin and (b) the point located at (-2.0, -2.0) m?View SolutionQuestion 69
At the instant the displacement of a 1.50 kg object relative to the origin is →d=(2.00m)ˆi+(4.00m)ˆj−(3.00m/s)ˆk, its velocity is →v=−(6.00m/s)ˆi+(3.00m/s)ˆj+(3.00m)ˆk and it is subject to a force →F=(6.00N)ˆi−(8.00N)ˆj+(4.00N)ˆk. Find (a) the acceleration of the object, (b) the angular momentum of the object about the origin, ( c) the torque about the origin acting on the object, and (d) the angle between the velocity of the object and the force acting on the object.View SolutionQuestion 70
In Fig. 10-72, a 0.400 kg ball is shot directly upward at initial speed 40.0 m/s. What is its angular momentum about P, 2.00 m horizontally from the launch point, when the ball is (a) at maximum height and (b) halfway back to the ground? What is the torque on the ball about P due to the gravitational force when the ball is ( c) at maximum height and (d) halfway back to the ground?
 View Solution
View SolutionQuestion 71
A particle is acted on by two torques about the origin: →τ1 has a magnitude of 2.0N⋅m and is directed in the positive direction of the x axis, and →τ2 has a magnitude of 3.0N⋅m and is directed in the nagative direction of the y axis. In unit-vector notation, find →dl/dt, where →l is the angular momentum of the particle about the origin.View SolutionQuestion 72
In Fig. 10-73, a particle of mass m is released from rest at point A, at distance b from the origin, and falls parallel to a vertical y axis. As a function of time t and with respect to the origin, find the magnitudes of (a) the torque τ on the particle due to the gravitational force and (b) the angular momentum L of the particle. ( c) From those results, verify that τ=dL/dt.
 View Solution
View SolutionQuestion 73
Figure 10-74 is an overhead view of a rod of length d and negligible mass that rotates at angular speed ω in the horizontal plane about a vertical axis through point O. Particle A of mass m is attached at the center point and an identical particle B is attached at the far end. Find the angular momentum of particle B with respect to particle A.
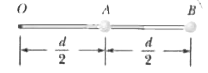 View Solution
View SolutionQuestion 75
Figure 10-75 shows three rotating, uniform disks that are coupled by belts. One belt runs around the rims of disks A and C. Another belt runs around a central hub on disk A and the rim of disk B. The belts move smoothly without slip-page on the rims and hub. Disk A has radius R, its hub has radius 0.5000R, disk B has radius 0.2500R, and disk C has radius 2.000 R. Disks B and C have the same density (mass per unit volume) and thickness. What is the ratio of the magnitude of the angular momentum of disk C to that of disk B?
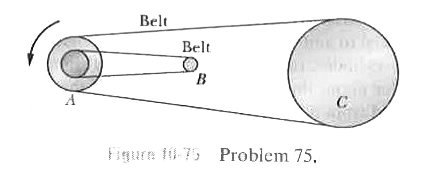 View Solution
View SolutionQuestion 76
In Figure, three particles of mass m = 23 g are fastened to three rods of length d = 12 cm and negligible mass. The rigid assembly rotates around point O at the angular speed ω=0.85rad/s. About O, what are (a) the rotational inertia of the assembly, (b) the magnitude of the angular momentum of the middle particle, and ( c) the magnitude of the angular momentum of the assembly?
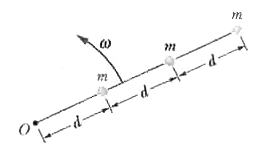 View Solution
View SolutionQuestion 77
A sanding disk with rotational inertia 8.6×10−3kg⋅m2 is attached to an electric drill whose motor delivers a torque of magnitude 16N⋅m about the central axis of the initially stationary disk. About that axis and with the torque applied for 33 ms, what is the magnitude of the (a) angular momentum and (b) angular velocity of the disk?View SolutionQuestion 78
The angular momentum of a flywheel having a rotational inertia of 0.140kg⋅m2 about its central axis decreases from 3.00 to 0.800kg⋅m2/s in 1.50 s. (a) What is the magnitude of the average torque acting on the flywheel about its central axis during this period? (b) Assuming a constant angular acceleration, through what angle does the flywheel turn? ( c) How much work is done on the wheel? (d) What is the average power of the flywheel?View SolutionQuestion 80
Figure 10-77 shows a rigid structure consisting of a circular hoop of radius R and mass m, and a square made of four thin bars, each of length R and mass m. The rigid structure rotates at a constant speed about a vertical axis, with a period of rotation of 2.5 s. Assuming R = 0.50 m and m = 2.0 kg, calculate (a) the structure's rotational inertia about the axis of rotation and (b) its angular momentum about that axis.
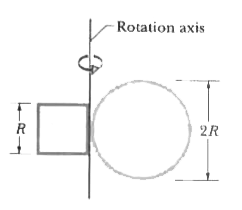 View Solution
View SolutionQuestion 81
In Fig. 10-78, two skaters, each of mass 50 kg, approach each other along parallel paths separated by 3.0 m. They have opposite velocities of 1.4 m/s each. One skater carries one end of a long pole of negligible mass, and the other skater grabs the other end as she passes. The skaters then rotate around the center of the pole. Assume that the friction between skates and ice is negligible. What are (a)the radius of the circle, (b) the angular speed of the skaters, and ( c) the kinetic energy of the two skater system? Next, the skaters pull along the pole unyil they are separated by 1.0 m. What then are (d) their angular speed and (e) the kinetic energy of the system? (f) What provided the energy for the increased kinetic energy?
 View Solution
View SolutionQuestion 82
A cockroach of mass 0.20 kg runs counterclockwise around the rim of a lazy Susan (a circular disk mounted on a vertical axle) that has radius 18 cm, rotational inertia 5.0×10−3kg⋅m2, and frictionless bearings. The cockroach's speed (relative to the ground) is 2.0 m/s, and the lazy Susan turns clockwise with angular speed ω0=2.8rad/s. The cockroach finds a bread crumb on the rim and, of course, stops. (a) What is the angular speed of the lazy Susan after the cockroach stops? (b) Is mechanical energy conserved as it stops?View SolutionQuestion 83
A man stands holding a weight in each hand and with his arms outstretched on a frictionless platform which is rotating at a speed of 1 revolution per sec. In ths position the total rotational intertia of the man, the weights and the platform is 6kgm2. If by drawing in his arms, the man decreases the rotational inertia of the system by 2kgm2, calcualte the resulting speed of the platform and the increase in kinetic energy. How do you account for the increase of kinetic energy? View SolutionQuestion 85
A track is mounted on a large wheel that is free to turn with neigligible friction about a vertical axis (Fig). A toy train of mass M is placed on the track and, with the system initially at rest, the train's electrical power is turned on. The train reaches speed v with respect to the track. What is the wheel's angular speed if its mass is m and its radius is r ? (Treat it as a hoop, and neglect the mass of the spokes and hub).
 .View Solution
.View SolutionQuestion 86
Two disks are mounted (like a merry-go-round) on low-friction bearings on the same axle and can be brought together so that they couple and rotate as one unit. The first disk, with rotational inertia 3.30kg⋅m2 about its central axis, is set spinning counterclockwise at 450 rev/min. The second disk, with rotational inertia 6.60kg⋅m2 about its central axis, is set spinning counterclockwise at 900 rev/min. They then couple together. (a) What is their angular speed after coupling? If instead the second disk is set spinning clockwise at 900 rev/min, what are their (b) angular speed and (c ) direction of rotation after they couple together?View SolutionQuestion 87
The rotor of an electric motor has rotational inertia Im=2.0×10−3kg⋅m2 about its central axis. The motor is used to change the orientation of the space probe in which it is mounted. The motor axis is mounted along the central axis of the probe, the probe has rotational inertia Ip=10kg⋅m2 about this axis. Calculate the number of revolutions of the rotor required to turn the probe through 30∘ about its central axis.View SolutionQuestion 88
A wheel of moment of inertia 0.10kg−m2 is rotating about a shaft at an angular speed o 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with as common angular speed of 200 rev/minute. Find the moment of inertia o the second wheel.View SolutionQuestion 89
A cockroach of mass m lies on the rim of a uniform disk of mass 4.00 m that can rotate freely about its center like a merry-goround. Initially the cockroach and disk rotate together with an angular velocity of 0.320 rad/s. Then the cockroach walks halfway to the center of the disk. (a) What then is the angular velocity of the cockroach-disk system? (b) What is the ratio K/K0 of the new kinetic energy of the system to its initial kinetic energy? ( c) What accounts for the change in the kinetic energy?View SolutionQuestion 90
Figure 10-80 is an overhead view of a rod with length 2L and negligible mass and which lies on a frictionless surface. Two bullets, each with mass m and speed v and traveling parallel to the x axis, hit the ends of the rod simultaneously and are buried in the rod. After the collision, what are (a) the angular speed of the system and (b) the speed of the system's center of mass? (c ) What is the change in the total kinetic energy because of the collisions?
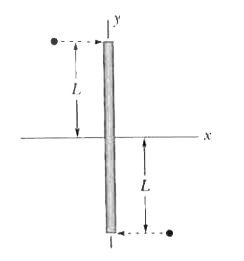 View Solution
View SolutionQuestion 91
Figure 10-81 shows an overhead view of a ring that can rotate about its center like a merry-go-round. Its outer radius R2 is 0.800 m, its inner radius R1 is R2/2.00, its mass M is 6.00 kg, and the mass of the crossbars at its center is negligible. It initially rotates at an angular speed of 8.00 rad/s with a cat of mass m = M/4.00 on its outer edge, at radius R2. By how much does the cat increase the kinetic energy of the cat-ring system if the cat crawls to the inner edge, at radius R1?
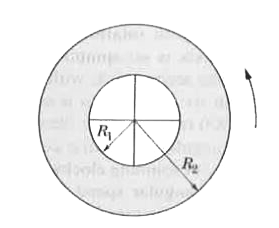 View Solution
View SolutionQuestion 92
Figure 10-82 is an overhead view of semicircular ring of mass m and radius R that lies on a frictionless surface. The ring is connected by elevated spokes (not shown) to a pivot at the center of the semicircle. The ring can rotate around that pivot but is initially stationary. A bead of mass m and speed v is shot into the ring, entering under the spokes and tangentially to the ring and then sliding along the ring. The ring and bead then rotate together around the pivot. Find their angular speed.
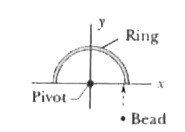 View Solution
View SolutionQuestion 93
A horizontal platform in the shape of a circular disk rotates on a frictionless bearing about a vertical axle through the centre of the disk. The platform has a mass of 150kg, a radius of 2.0m, and a rotational inertia of300kgm2 about the axis of rotation. A 60kg student walks slowly from the rim of the platform toward the centre. If the angular speed of the system is 1.5rad/s when the student starts at the rim, what is the angular speed when she is 0.50m from the centre ?View SolutionQuestion 94
Figure 10-83 is an overhead view of a spring lying on a frictionless surface and attached to a pivot at its right end. The spring has a relaxed length of l0=1.00 and negligible mass. A small 0.100 kg disk is attached to the free end at the left. That disk is then given a velocity →v0 of magnitude 11.0 m/s perpendicular to the spring's length. The disk and spring then move around the pivot. (a) When the stretching of the spring reaches its maximum value of 0.100l0, what is the speed of the disk? (b) What is the spring constant?
 View Solution
View SolutionQuestion 95
In Fig. 10-84, a 1.0 g bullet is fired into a 0.60 kg block attached to the end of a 0.75 m nonuniform rod of mass 0.50 kg. The block-rod-bullet system then rotates in the plane of the figure, about a fixed axis at A. The rotational inertia of the rod alone about that axis at A is 0.060kg⋅m2. Treat the block as a particle. (a) What then is the rotational inertia of the block-rod-bullet system about point A? (b) If the angular speed of the system about A just after impact is 4.5 rad/s, what is the bullet's speed just before impact?
 View Solution
View SolutionQuestion 96
The uniform rod (length 0.60 m, mass 1.0 kg) in Fig. 10-85 rotates in the plane of the figure about an axis through one end, with a rotational inertia of 0.12kg⋅m2. As the rod swings through its lowest position, it collides with a 0.20 kg putty wad that sticks to the end of the rod. If the rod's angular speed just before collision is 2.4 rad/s, what is the angular speed of the rod-putty system immediately after collision?
 View Solution
View SolutionQuestion 97
In Fig. 10-86, a 30 kg child stands on the edge of a stationary merry-go-round of radius 2.0 m. The rotational inertia of the merry-go-round about its rotation axis is 150kg⋅m2. The child catches a ball of mass 1.0 kg thrown by a friend. Just before the ball is caught, it has a horizontal velocity →v of magnitude 12 m/s, at angle ϕ=37∘ with a line tangent to the outer edge of the merry-go-round, as shown. What is the angular speed of the merry-go-round just after the ball is caught?
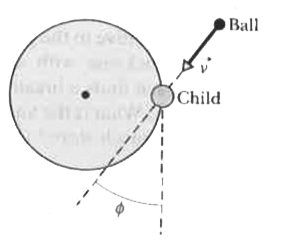 View Solution
View SolutionQuestion 98
Two 2.00 kg balls are attached to the ends of a thin rod of length 50.0 cm and negligible mass. The rod is free to rotate in a vertical plane without friction about a horizontal axis through its center. With the rod initially horizontal (Fig. 10-87), a 50.0 g wad of wet putty drops onto one of the balls, hitting it with a speed of 3.00 m/s and then sticking to it. (a) What is the angular speed of the system just after the putty wad hits? (b) What is the ratio of the kinetic energy of the system after the collision to that of the putty wad just before? ( c) Through what angle will the system rotate before it momentarily stops?
 View Solution
View SolutionQuestion 99
In the shown figure a mass m slides down the frictionless surface from height h and collides with the uniform vertical rod of length L and mass M after collision the mass m sticks to the rod. The rod is face to rotate in a vertical plane about fixed axis through O. Find the maximum angular deflection of the rod from its initial position.
 View Solution
View SolutionQuestion 100
A top spins at 25 rev/s about an axis that makes an angle of 30∘ with the vertical. The mass of the top is 0.50 kg, its rotational inertia about its central axis is 5.0×10−4kg⋅m2, and its center of mass is 4.2 cm from the pivot point. If the spin is clockwise from an overhead view, what are the (a) precession rate and (b) direction of the precession as viewed from overhead?View Solution