For the circuit shown in Fig. determine the branch voltage and currents and power delivered by the source using mesh analysis.
Let the mesh currents be as shown in Fig.. The different items of the mesh resistance matrix [Em] are : Z11 = 2 + j1 + j2 −j1 = 2 + j2 Z22 = −j2 + 1 −j1 + j2 = 1 −j1 Z12 = Z21 = − j2 −j1 = −j1 Hence the mesh equations in the matrix form are= 5.46∠− 135º or ∠225º I1 = Δ1/Δ = 19.1 ∠− 49.1º/5 = 3.82 ∠−49.1º = 2.5 – j2.89 I2 = Δ2/Δ = 5.46 ∠− 135º/5 = 1.1 ∠−135º = − 0.78 −j0.78 Current through branch BC = I1−I2 = 2.5 −j2.89 + 0.78 + j0.78 = 3.28 −j2.11 = 3.49 ∠− 32.75º Drop over branch AB = 2 + j12.5 −j 2.89 = 7.89 −j 3.28 Drop over branch BD = 1 −j2 −0.78 −j0.78 = 2.34 + j0.78 Drop over branch BC = j 1 I1 −I2 = j1 3.28 −j2.11 = 2.11 + j3.28 Power delivered by the sources would be found by using conjugate method. Using current conjugate we getVA1 = 102.5 + j2.89 = 25 + j28.9 ; ∴ W1 = 25 W VA2 = V2 × I2 — because –I2 is the current coming out of the second voltage source. Again using current conjugate we have VA2 = 4.43 + j2.5 0.78 −j0.78 or W2 = 4.43 × 0.78 + 2.5 × 0.78 = 5.4 W ∴ total power supplied by the two sources = 25 + 5.4 = 30.4 W Incidentally the above fact can be verified by adding up the powers dissipated in the three branches of the circuit. It may be noted that there is no power dissipation in the branch BC. Power dissipated in branch AB = 3.822 × 2 = 29.2 W Power dissipated in branch BD = 1.12 × 1 = 1.21 W Total power dissipated = 29.2 + 1.21 = 30.41 W.
Related Solutions
Determine the current in each branch of the network shown in Fig.
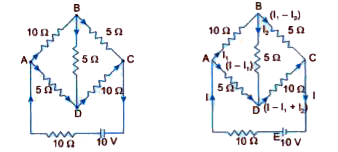 View Solution
View SolutionDetermine the current in each branch of the network shown in fig.
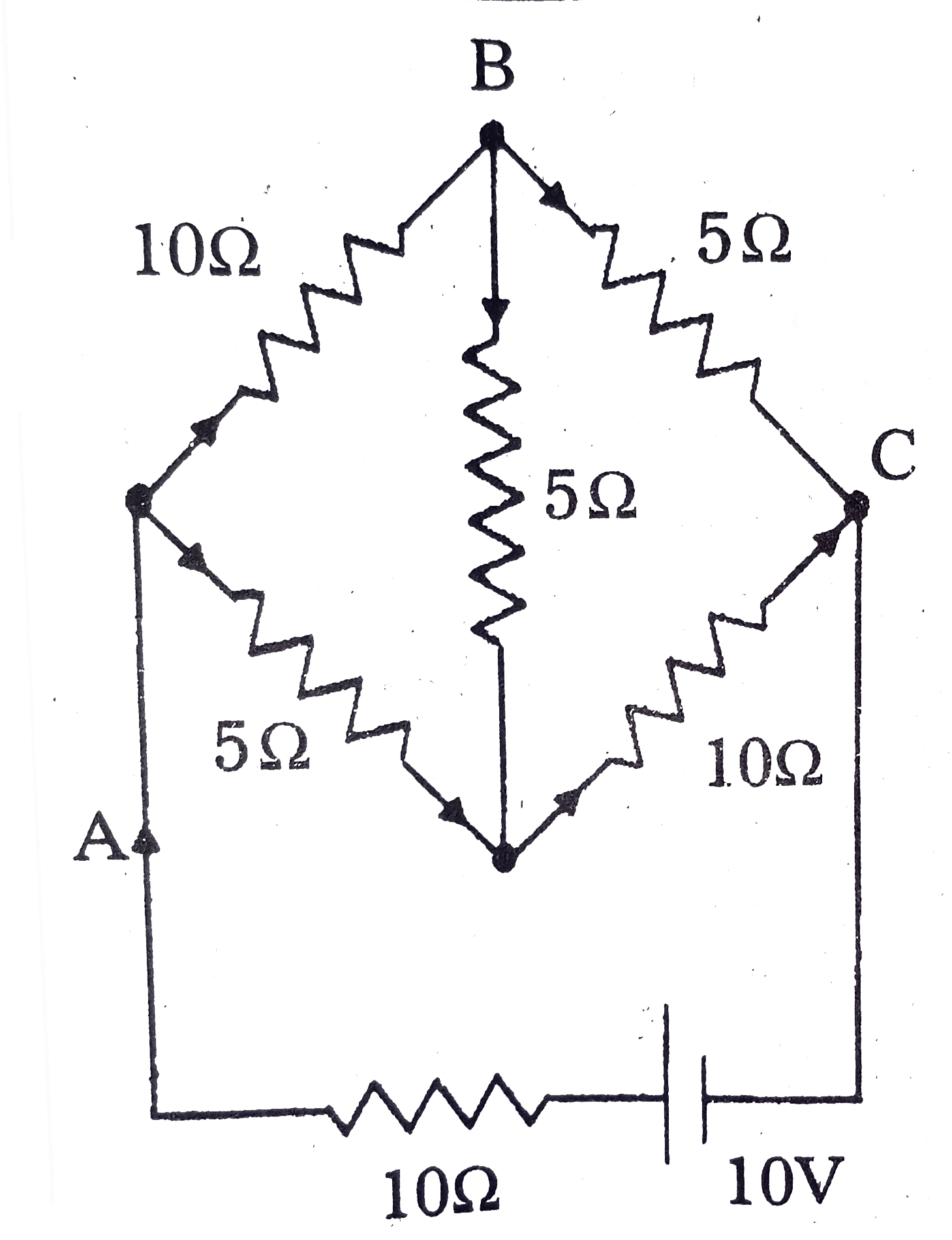 View Solution
View SolutionDetermine the current in each branch of the network shown in Fig.
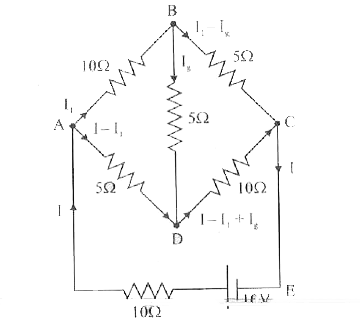 View Solution
View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in fig.
View Solution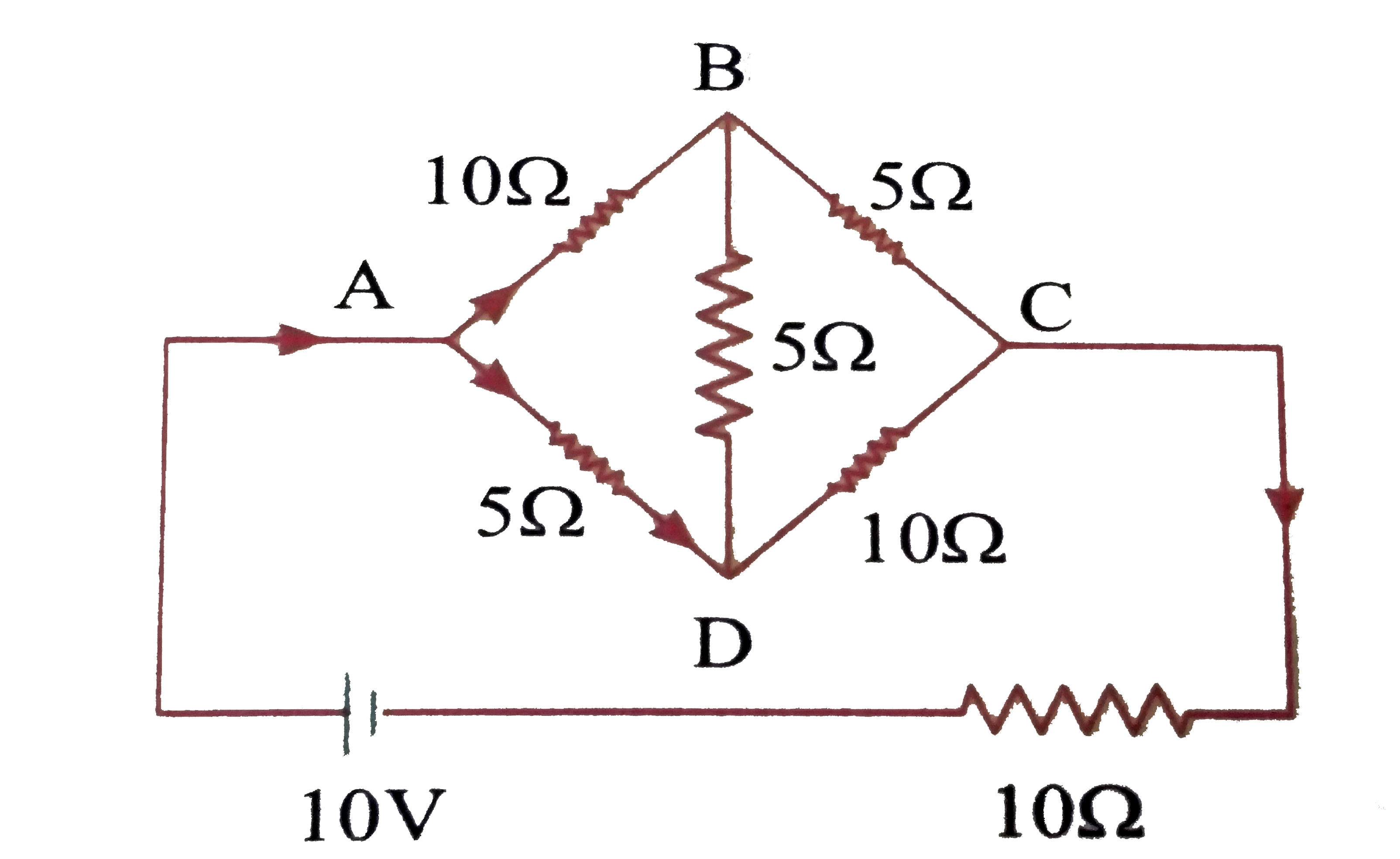
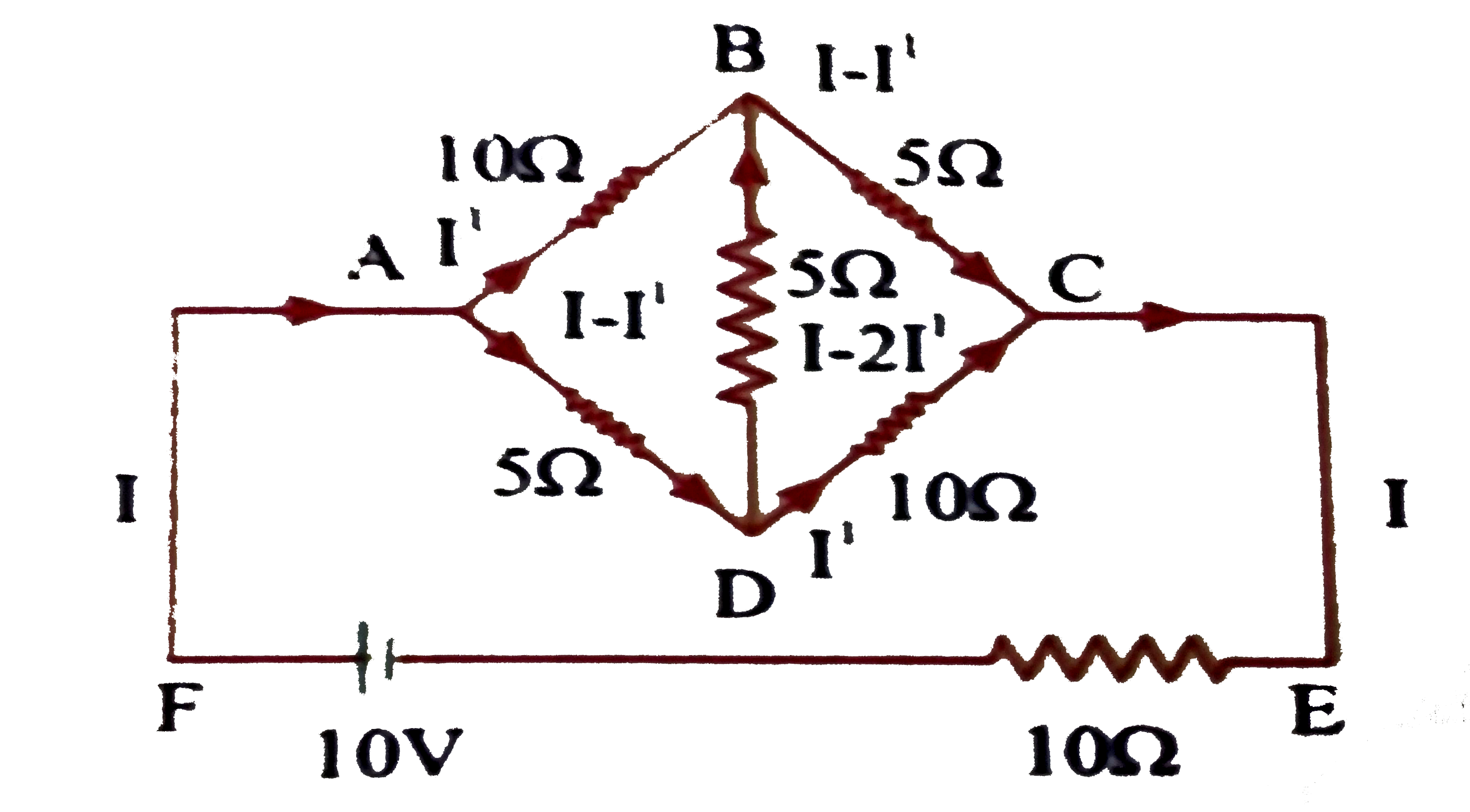
Determine the current in each branch of the network shown in fig.View SolutionDetermine the current in each branch of the network shown in Fig.
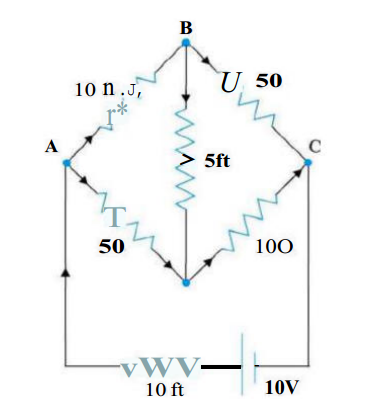 View Solution
View SolutionWhat is the amount of power delivered by the ac source in the circuit shown (in watts)
 View Solution
View SolutionWhat is the amount of power delivered by the ac source in the circuit shown (in watts)
 View Solution
View SolutionWhat is the amount of power delivered by the ac source in the circuit shown (in watts)
View SolutionDetermine the currents through the resistance of the circuits shown in fig.
View SolutionIn the circuit shown in fig. find the current through the branch BD.
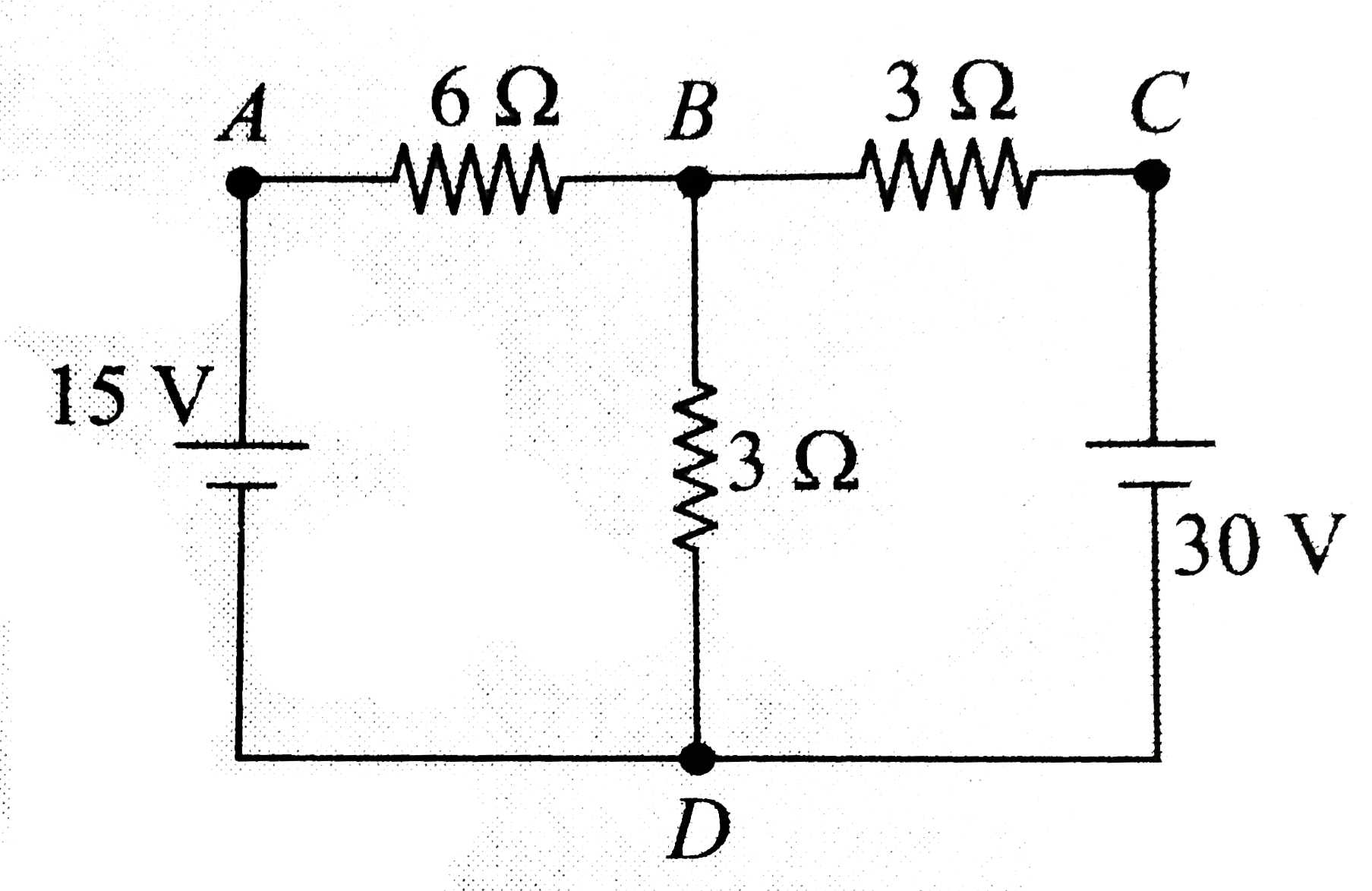 View Solution
View SolutionDetermine the current in branches AB and BC of the network shown in Fig.
View SolutionDetermine the current in each branch of the network shown in Fig. 3.24
 View Solution
View SolutionIn the circuit shown in Fig. 5.79, determine the voltage drop between A and D.
View SolutionIn the circuit shown in Fig. 5.79, determine the voltage drop between A and D.
View SolutionThere is an AC source of rms voltage 200 V and frequency 50 Hz. When the source is connected to a circuit then rms current flowing in the circuit is 15 A. Average power delivered by the source
View SolutionCalculate the current delivered by the voltage source in the following networks.
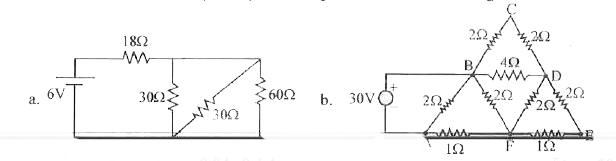 View Solution
View SolutionThe power delivered by the source of a LCR circuit is maximam when'
View Solutionकिसी ac स्रोत द्वारा परिपथ को दी गई शक्ति का मान अधिकतम होगा, यदि
View Solution
