Find the total heat produced in the loop of the previous problem during the interval 0 to 30s if the resistance of the loop is 4.5mΩ.
As heat produced is a scalar prop.So net heat produced = Ha + Hb + Hc + HdR = 4.5mΩ = 4.5 ×10–3Ωa e = 3 × 10–4 VHa = 6.7 ×10–22 × 4.5 × 10–3 × 5Hb = Hd = 0 [since emf is induced for 5sec]Hc = 6.7 ×10–22 × 4.5 × 10–3 × 5So Total heat = Ha + Hc= 2 × 6.7 ×10–22 × 4.5 × 10–3 × 5 = 2 × 10–4J.
Related Solutions
Find the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mOmega.
View SolutionFind the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mOmega.
View SolutionFind the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mOmega.
View SolutionFind the total heat produced in the loop of the previous problem during the interval to
View SolutionFind the total heat produced in the loop of the previous problem during the interval 0 to 5s
View SolutionIn the previous problem, fin dthe total heat produced in the loop.
View SolutionA magentic flux through a statinary loop with a resistance varies during the tiem interval as . Find the amount of heat generated in the loop during that time. The inductance of the loop is to be neglected.
View SolutionA magnetic flux through a stationary loop with a resistance varies during the time interval as . Find the amount of heat the generated in the loop during that time
View SolutionMagnetic flux through a stationary loop with a resistance R varies during the time interval tau" as "phi=alphat(tau-t) where alpha is a constant. Calculate the amount of heat generated in the loop during the time interval tau .
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from according to law . If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from according to law . If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.View SolutionR प्रतिरोध वाले स्थायी लूप में से चुम्बकीय फ्लक्स के रूप में समय अन्तराल के दौरान परिवर्तित होता है। उस समय के दौरान लूप में उत्पन्न ऊष्मा की मात्रा क्या है?
View SolutionThe magnetic flux through a stationary loop with resistance R varies during interval of time T as phi = at (T – t). The heat generated during this time neglecting the inductance of loop will be
View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval tau as phi = at (tau-t) What is the amount of heat generated in the loop during that time?
View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval tau as phi=at(tau-t) . Find the amount of the generated in the loop during that time
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View SolutionA triangle loop as shown in the figure is started to being pulled out at from a uniform magnetic field with a constant velocity .Total resistance of the loop is constant and equals to .Then the variation of power produced in the loop with time will be:
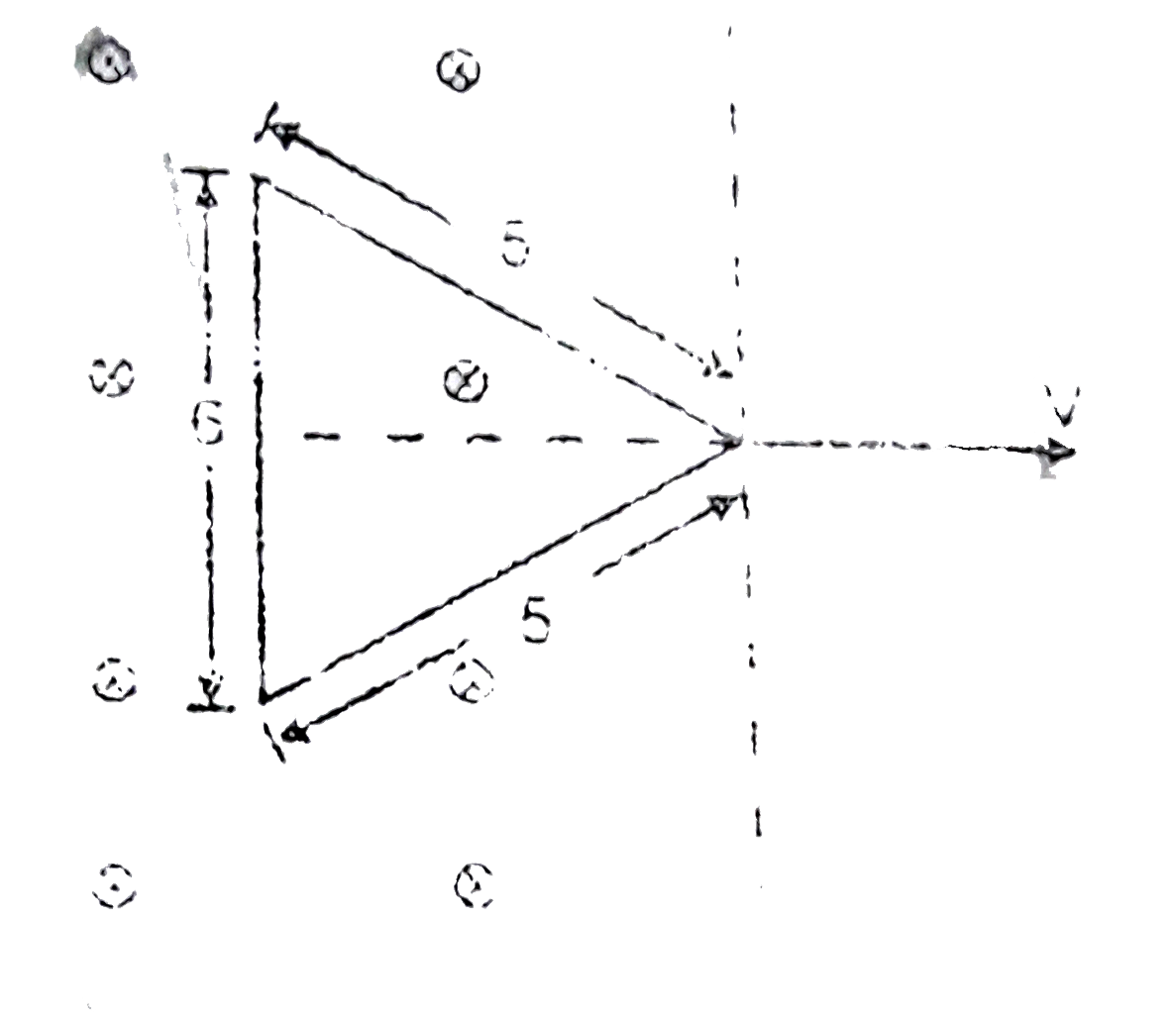 View Solution
View SolutionWith time t the magnetic flux associated with a stationary loop of resistance R phi =at(T-t) converts as. The amount of heat generated in the loop during the time interval T is:
View SolutionA constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v . a Find induced emf produced i the loop as a function x b. If total resistance of the loop is R , then find induced current in the loop,
View Solution
