A magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of heat the generated in the loop during that time
aτ22R
a2τ23R
2a2τ33R
aτ3R
The correct Answer is:B
To solve the problem, we need to find the amount of heat generated in a loop with resistance R when the magnetic flux ϕ varies with time as given by the equation ϕ=at(τ−t).
1. Find the EMF (Electromotive Force):
The EMF E induced in the loop can be calculated using Faraday's law of electromagnetic induction, which states that the induced EMF is equal to the negative rate of change of magnetic flux:
E=−dϕdt
Given ϕ=at(τ−t), we differentiate ϕ with respect to t:
dϕdt=a(τ−t)+at(−1)=a(τ−2t)
Therefore, the induced EMF is:
E=−a(τ−2t)
2. Calculate the Current (I):
Using Ohm's law, the current I flowing through the loop can be expressed as:
I=ER=−a(τ−2t)R
3. Calculate the Heat Generated (H):
The heat generated in the resistor over the time interval τ can be calculated using the formula:
H=∫τ0I2Rdt
Substituting for I:
H=∫τ0(−a(τ−2t)R)2Rdt
Simplifying this gives:
H=a2R∫τ0(τ−2t)2dt
4. Evaluate the Integral:
We need to evaluate the integral ∫τ0(τ−2t)2dt:
(τ−2t)2=τ2−4τt+4t2
Thus,
∫τ0(τ−2t)2dt=∫τ0(τ2−4τt+4t2)dt
Evaluating this integral term by term:
- The first term: ∫τ0τ2dt=τ2⋅t∣∣τ0=τ3
- The second term: ∫τ0−4τtdt=−4τ⋅t22∣∣τ0=−2τ3
- The third term: ∫τ04t2dt=4⋅t33∣∣τ0=4τ33
Combining these results:
∫τ0(τ−2t)2dt=τ3−2τ3+4τ33=(1−2+43)τ3=−2+431τ3=−6+43τ3=−23τ3
5. Final Calculation of Heat (H):
Substituting back into the equation for H:
H=a2R⋅23τ3=2a2τ33R
Final Answer:
The amount of heat generated in the loop during the time interval τ is:
H=2a2τ33R
The EMF E induced in the loop can be calculated using Faraday's law of electromagnetic induction, which states that the induced EMF is equal to the negative rate of change of magnetic flux:
E=−dϕdt
Given ϕ=at(τ−t), we differentiate ϕ with respect to t:
dϕdt=a(τ−t)+at(−1)=a(τ−2t)
Therefore, the induced EMF is:
E=−a(τ−2t)
Using Ohm's law, the current I flowing through the loop can be expressed as:
I=ER=−a(τ−2t)R
The heat generated in the resistor over the time interval τ can be calculated using the formula:
H=∫τ0I2Rdt
Substituting for I:
H=∫τ0(−a(τ−2t)R)2Rdt
Simplifying this gives:
H=a2R∫τ0(τ−2t)2dt
We need to evaluate the integral ∫τ0(τ−2t)2dt:
(τ−2t)2=τ2−4τt+4t2
Thus,
∫τ0(τ−2t)2dt=∫τ0(τ2−4τt+4t2)dt
Evaluating this integral term by term:
- The first term: ∫τ0τ2dt=τ2⋅t∣∣τ0=τ3
- The second term: ∫τ0−4τtdt=−4τ⋅t22∣∣τ0=−2τ3
- The third term: ∫τ04t2dt=4⋅t33∣∣τ0=4τ33
∫τ0(τ−2t)2dt=τ3−2τ3+4τ33=(1−2+43)τ3=−2+431τ3=−6+43τ3=−23τ3
Substituting back into the equation for H:
H=a2R⋅23τ3=2a2τ33R
The amount of heat generated in the loop during the time interval τ is:
H=2a2τ33R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represent by
View SolutionThe magnetic field through a single loop of wire, 12cm in radius and of 8.5Ω resistance, changes with time as shown in figure. Calculate the emf in the loop as a function of time. Consider the time intervals
(a) t=0 to t=2.0s (b) t=2.0s to t=4.0s (c) t=4.0s to t=6.0s.
The magnetic field is perpendicular to the plane of the loop.

View Solution
Knowledge Check
The charge flowing through a resistance R varies with time t as Q=at−bt2. The total heat produced in R is
Aa3RbBa3R2bCa3R3bDa3R6bThe magnetic flux through a coil perpendicluar to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
A0.12 VB2.4 VC0.02 VD1.2 V
Current passing through a resistor of resistance 5Ω varies with time as shown in the graph.Heat generated in the resistance during 3s is equal to
_PHY_E05_283_Q01.png)
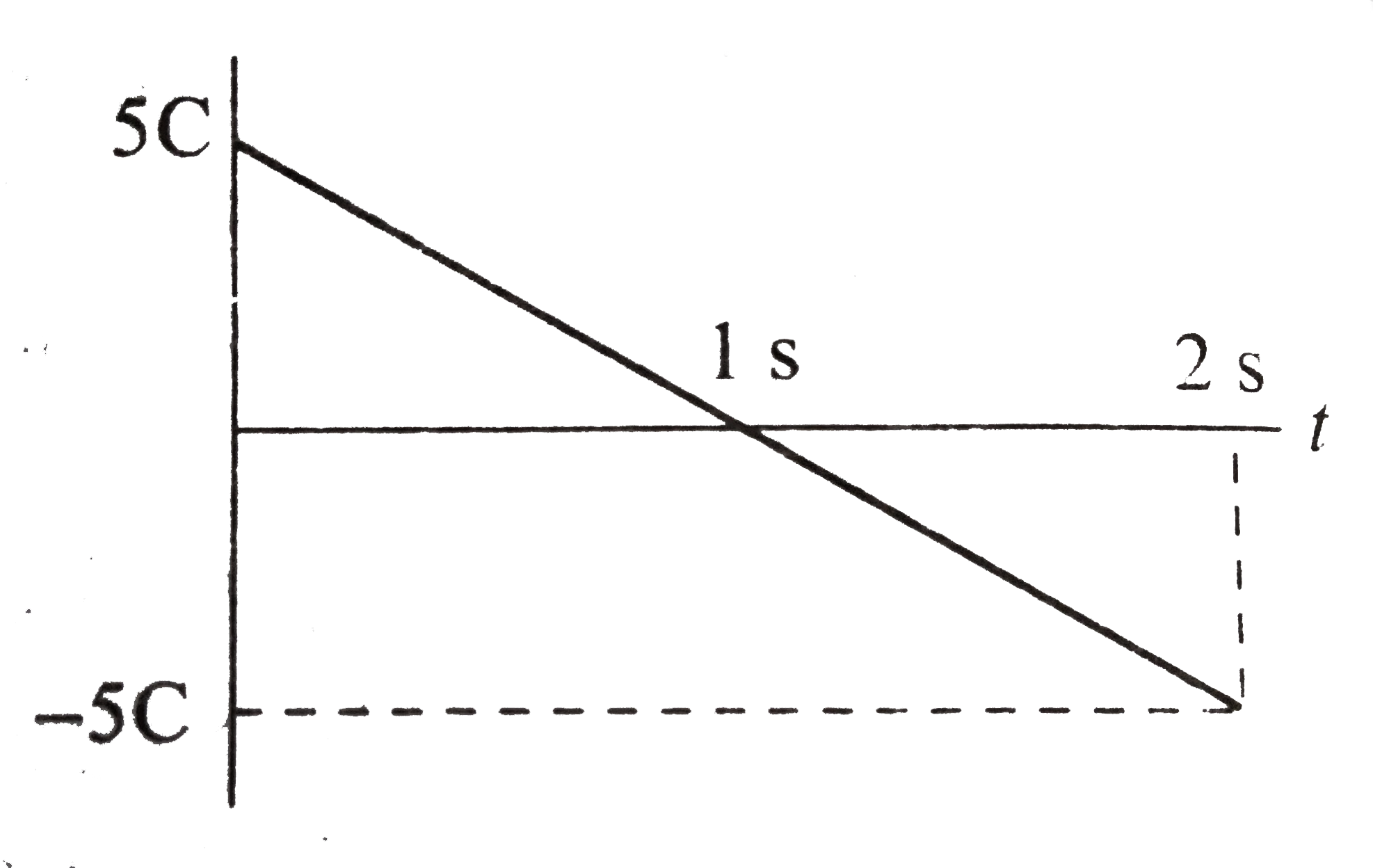
View SolutionA charge passing through a resistor varies with time as shown in the figure. The amount of heat generated in time t is best represented (as a function of time ) by
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.
View SolutionA triangular loop as shown in the figure is started to being pulled out at t=0 form a uniform magnetic field with a constant velocity v. Total resistancee of the loop is constant and equal to R. Then the variation of power produced in the loop with time will be :

View SolutionThe charge Q( in coulomb) flowing through a resistance R=10Ω varies with time t (in second) as Q=2t−t2 . The total heat produced in resistance R is
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View Solution
