Find the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mOmega.
To find the total heat produced in the loop during the interval from 0 to 30 seconds, we will follow these steps:
Step 1: Calculate the EMF
From the previous problem, we have the electromotive force (EMF) calculated as:
E=3×10−4 volts
Step 2: Calculate the Current
Using Ohm's law, the current I can be calculated using the formula:
I=ER
Where:
- E=3×10−4 volts
- R=4.5×10−3 ohms
Substituting the values:
I=3×10−44.5×10−3=6.67×10−2 amperes
Step 3: Calculate the Heat Produced
The heat produced H in the resistor can be calculated using the formula:
H=I2RT
Where:
- I=6.67×10−2 amperes
- R=4.5×10−3 ohms
- T=30 seconds
Substituting the values:
H=(6.67×10−2)2×(4.5×10−3)×30
Calculating (6.67×10−2)2:
(6.67×10−2)2=4.4489×10−3
Now substituting back into the heat equation:
H=4.4489×10−3×4.5×10−3×30
Calculating:
H=4.4489×10−3×0.0000045×30
H=6.0×10−7 joules
Step 4: Total Heat Produced
Since the problem mentions heat produced in the loop, if we consider the heat produced over the entire interval of 30 seconds, we can conclude that the total heat produced is:
Htotal=H×number of cycles
Assuming one cycle in this case, the total heat produced is:
Htotal=6.0×10−7 joules
Final Answer
The total heat produced in the loop during the interval from 0 to 30 seconds is:
Htotal=6.0×10−7 joules
---
From the previous problem, we have the electromotive force (EMF) calculated as:
E=3×10−4 volts
Using Ohm's law, the current I can be calculated using the formula:
I=ER
Where:
- E=3×10−4 volts
- R=4.5×10−3 ohms
I=3×10−44.5×10−3=6.67×10−2 amperes
The heat produced H in the resistor can be calculated using the formula:
H=I2RT
Where:
- I=6.67×10−2 amperes
- R=4.5×10−3 ohms
- T=30 seconds
H=(6.67×10−2)2×(4.5×10−3)×30
Calculating (6.67×10−2)2:
(6.67×10−2)2=4.4489×10−3
H=4.4489×10−3×4.5×10−3×30
Calculating:
H=4.4489×10−3×0.0000045×30
H=6.0×10−7 joules
Since the problem mentions heat produced in the loop, if we consider the heat produced over the entire interval of 30 seconds, we can conclude that the total heat produced is:
Htotal=H×number of cycles
Assuming one cycle in this case, the total heat produced is:
Htotal=6.0×10−7 joules
The total heat produced in the loop during the interval from 0 to 30 seconds is:
Htotal=6.0×10−7 joules
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when <AOC=90∘.
View SolutionConsider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
View Solutionsuppose the ends of the coil in the previous problem are connected to a resistane of 100Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
View SolutionA square loop of side a and straight infinity conductor are placed in the same plane with two sides of the square parallel to the conductor. The resistance of the loop is R. The loop is turned through 180∘ about the axis . The electric charge that flows in the square loop is μ0Ia2πR1m∣∣∣na+bb∣∣∣. Find the value of n.
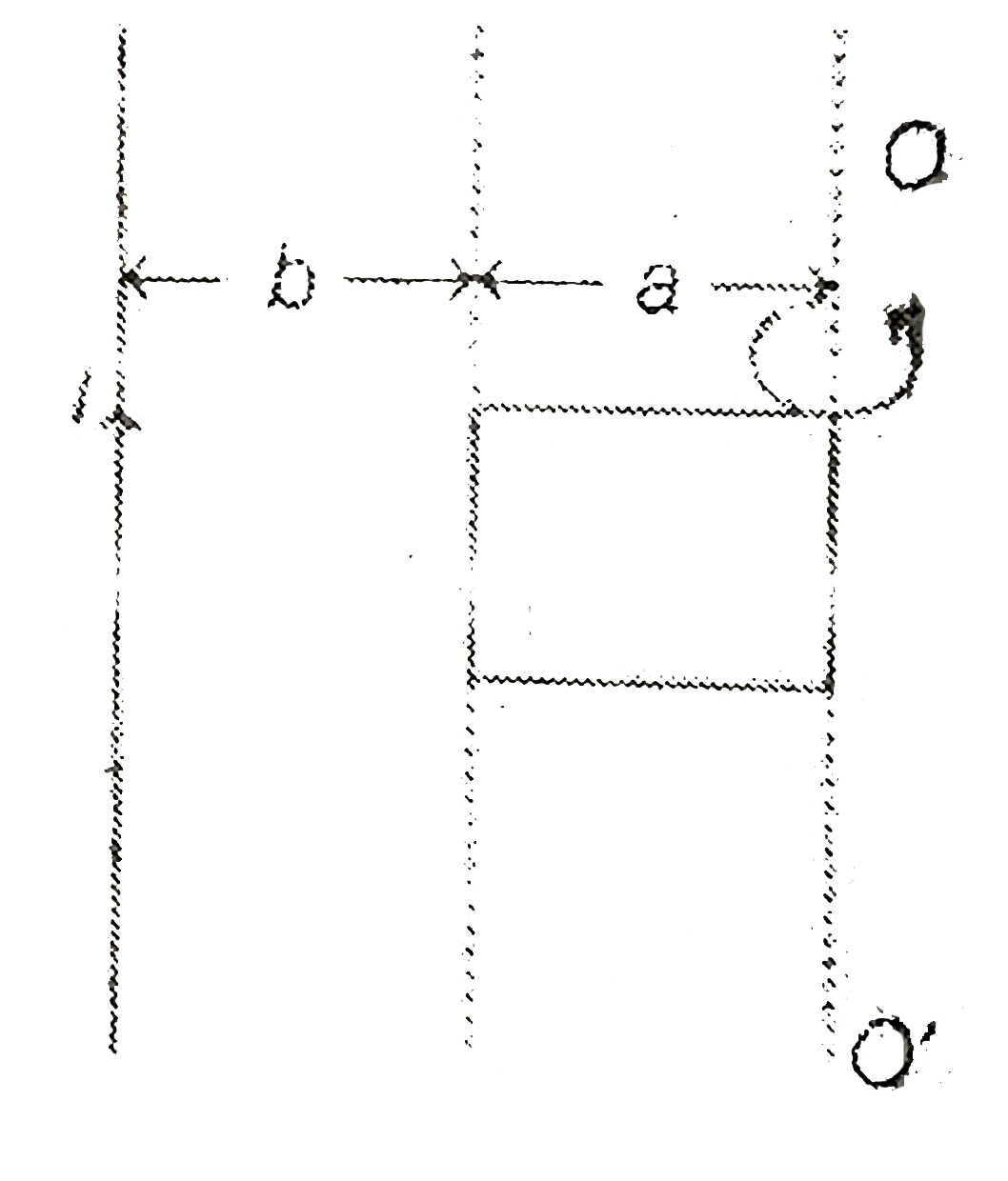
View SolutionCurrent in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find
a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.
View SolutionA constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v.

a Find induced emf produced i the loop as a function x
b. If total resistance of the loop is R, then find induced current in the loop,
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.
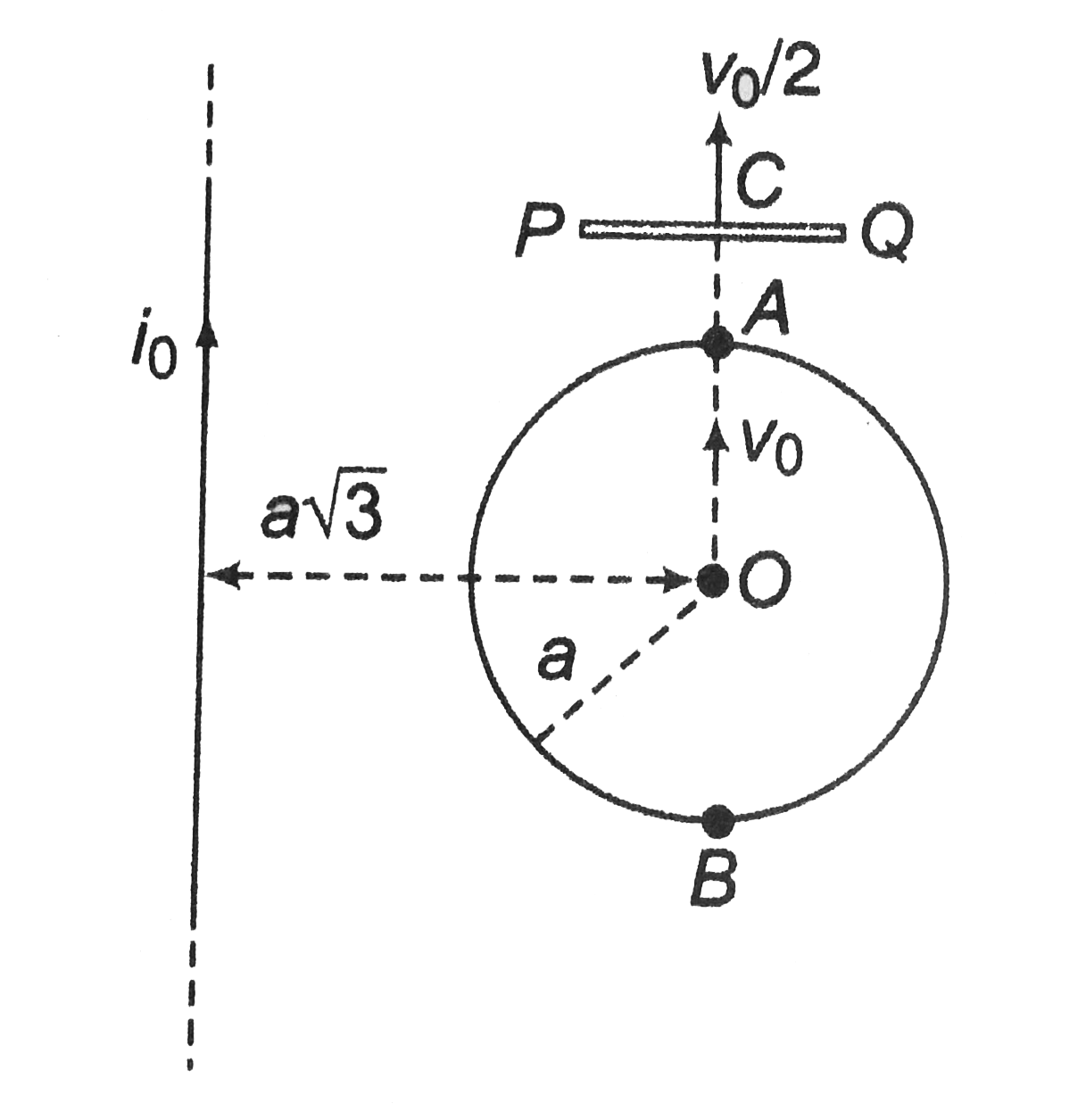
(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionA square shaped, conducting wire loop of side L, total mass m and total resistance R initially lies in the horizontal x−y plane, with corners at (x,y,z)=(0,0,0),(0,L,0),(L,0,0),and(L,L,0). There is a uniform upward magnetic field in the space within and around the loop. The side of the loop that extends from (0,0,0)→(L,0,0) is held in place on the x-axis, the rest of the loop is released, it begins to rotate due to the gravitational torque.
(a) Find the net torque (magnitude and direction)that acts on the loop when it has rotated through an anglr ϕ from its original orientation and is rotating dounward at an angular speed ω.
(b) Find the angular acceleration of the loop at the instant described in part (a).
( c) Compared to teh case with zero magnetic field, does it take the loop a longer or shorter time to rotate through 90∘ ? Explain.
(d) Is mechanical energy conserved as the loop rotates downward ? Explain.
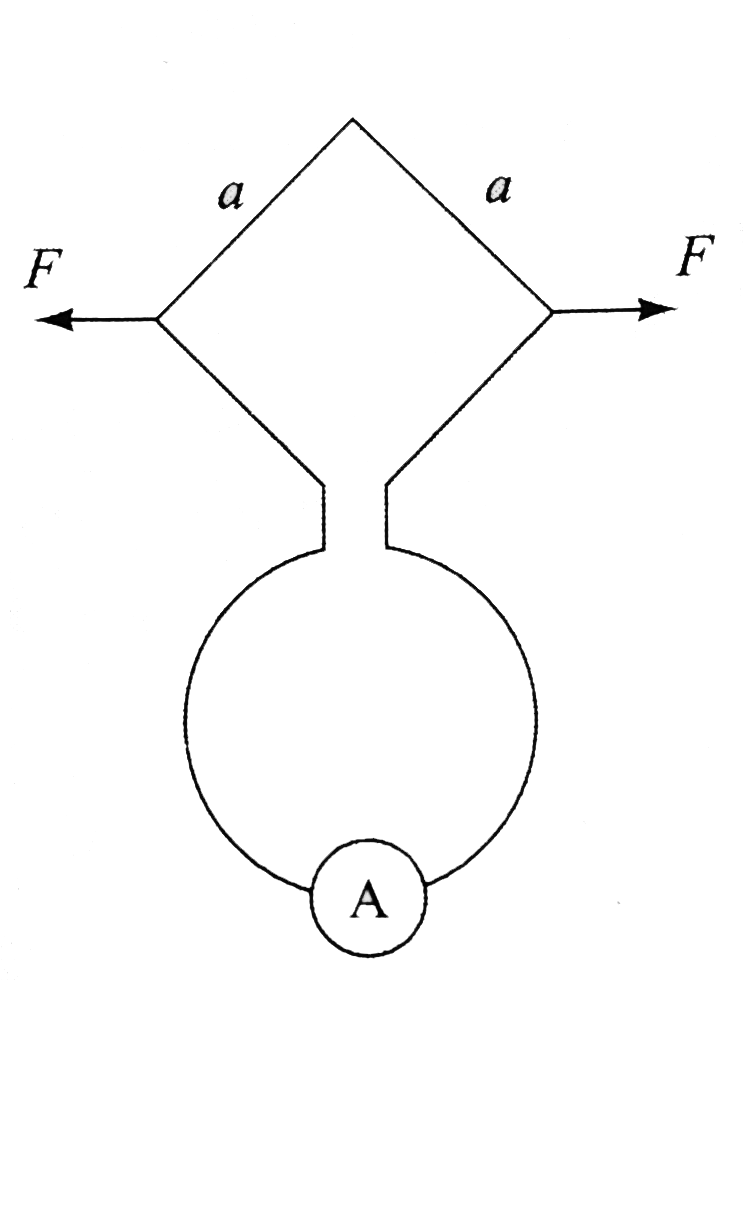
View SolutionThe plane of a square loop of wire edge length a=0.200m is perpendicualr to the Earth's magnetic field at a point where B=15.0μT, as shown in . The total resistance of the loop and the wires connecting it to a sensitive ammeter is 0.50Ω. If the loop is suddenly collapsed by horizontal forces as shown, what is the total charge passing through the ammeter?
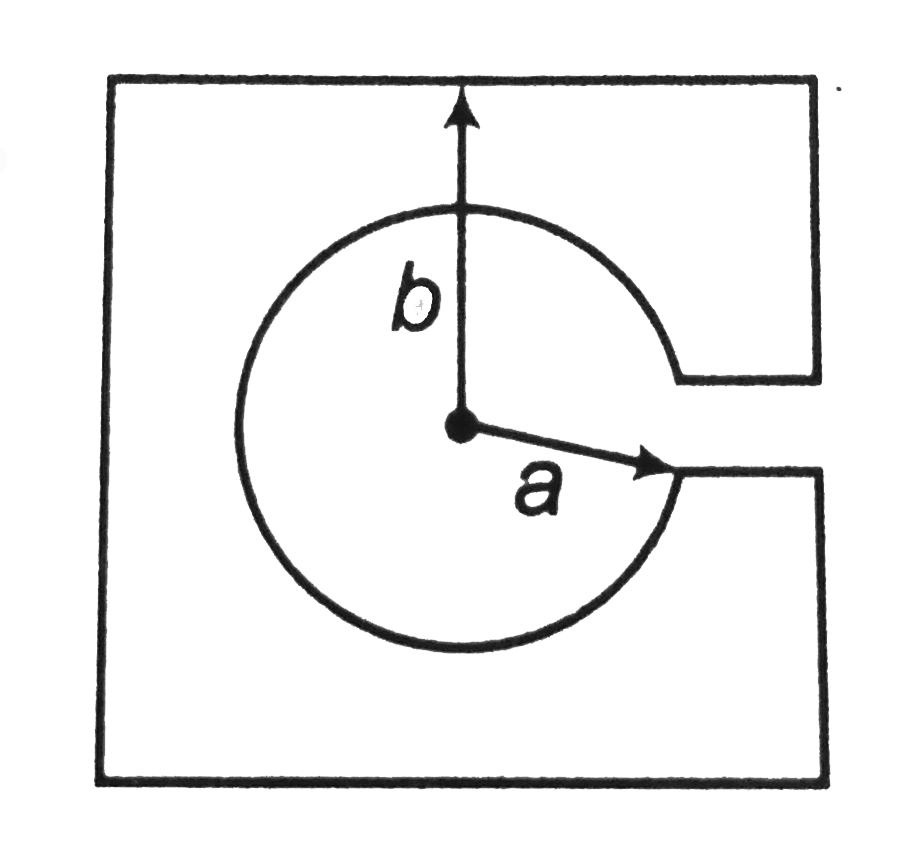
View SolutionA loop shown in the figure is immersed in the varying magnetic field B=B0t, directed into the page. If the total resistance of the loop is R, then the direction and magnitude of induced current in the inner circle is
View Solution
