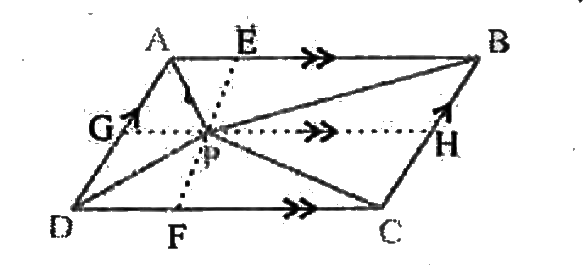
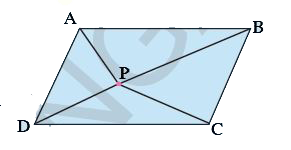
In the given figure P is a point in the interior of a parallelogram ABCD. Show thati ar APB + ar PCD = 1/2 ar ABCDii ar APD + ar PBC = ar APB + ar PCD [Hint: Through. P draw a line parallel to AB]
i Let us draw a line segment EF passing through point P and parallel to line segment AB.In parallelogram ABCD AB || EF By construction ... 1 ABCD is a parallelogram.∴ AD || BC Opposite sides of a parallelogram⇒ AE || BF ... 2From equations 1 and 2 we obtainAB || EF and AE || BFTherefore quadrilateral ABFE is a parallelogram.It can be observed that ΔAPB and parallelogram ABFE are lying on the same base AB and between the same parallel lines AB and EF.∴ Area ΔAPB = 1/2 Area ABFE ... 3 Similarly for ΔPCD and parallelogram EFCD Area ΔPCD 1/2 Area EFCD ... 4Adding equations 3 and 4 we obtainLet us draw a line segment MN passing through point P and parallel to line segment AD.In parallelogram ABCD MN || AD By construction ... 6ABCD is a parallelogram.∴ AB || DC Opposite sides of a parallelogram⇒ AM || DN ... 7From equations 6 and 7 we obtain MN || AD and AM || DNTherefore quadrilateral AMND is a parallelogram.It can be observed that ΔAPD and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.∴ Area ΔAPD = 1/2 Area AMND ... 8 Similarly for ΔPCB and parallelogram MNCB Area ΔPCB = 1/2 Area MNCB ... 9Adding equations 8 and 9 we obtainOn comparing equations 5 and 10 we obtainArea ΔAPD + Area ΔPBC = Area ΔAPB + Area ΔPCD
Related Solutions
दिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की

View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View Solutionआकृति में में समांतर चतुर्भुज के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i)
(ii)

View SolutionIn P is a point in the interior of a parallelogram ABCD. Show thatar (APD) + ar (PBC) = ar (APB) + ar (PCD)
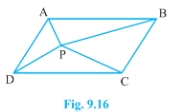
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) (ii)
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
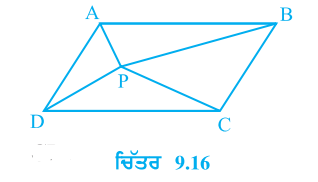
View Solutionਚਿੱਤਰ 9.16 ਵਿਚ, ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਅੰਦਰ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ P ਹੈ। ਦਰਸਾਉ ਕਿ (i) (ii) [ਸੰਕੇਤ:-P ਵਿੱਚੋਂ ਲੰਘਦੀ AB ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ।]
View SolutionIn the given figure, P is any point located in the interior of the parallelogram ABCD. Indicate that (i) ar (Delta APB ) + ar (Delta PCD ) = (1)/(2) (ar||^(g m)ABCD) (Ii) ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD)
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that ar (APB) + ar (PCD) = 1/(2) ar (ABCD)
View Solutionआकुति में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है दर्शाइए कि
Ar (APB ) + ar
View SolutionP is a point in the interior of a parallelogram ABCD. Show that ar (Delta APD) + ar ( DeltaPBC) = ar ( DeltaAPB) + ar (DeltaPCD)
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar = ar .
View SolutionDiagonals AC and BD of a quadrilateral ABCD each other at P. Show that ar (APB) ar (CPD) =ar (APD) ar (BPC)
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) ar (CPD) = ar (APD) ar (BPD).
[Hint : From A and C, draw perpendiculars to BD.
View Solutionਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ P 'ਤੇ ਕੱਟਦੇ ਹਨ। ਦਰਸਾਉ ਕਿ ar (APB) × ar (CPD) = ar (APD) × ar (BPC) ਹੈ। [ਸੰਕੇਤ: A ਅਤੇ C ਤੋਂ BD ਉੱਤੇ ਲੰਬ ਖਿੱਚੋ।
View SolutionP is a point in the interior of a parallelogram ABCD. Show that
(i) ar
(ii)
(Hint : Throught , P draw a line parallel to AB)
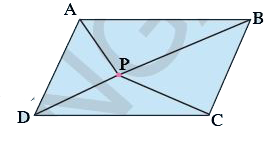
View SolutionP is a point in the interior of a parallelogram ABCD. Show that
(i) ar
(ii)
(Hint : Throught , P draw a line parallel to AB)

View SolutionP is a point in the interior of a parallelogram ABCD. Show that
(i) ar
(ii)
(Hint : Throught , P draw a line parallel to AB)
View SolutionIf P and P are points on the sides DC and AD of parallelogram ABCD respectively, show that ar( Delta APB) = ar(Delta BQC) Is.
View Solution