Question

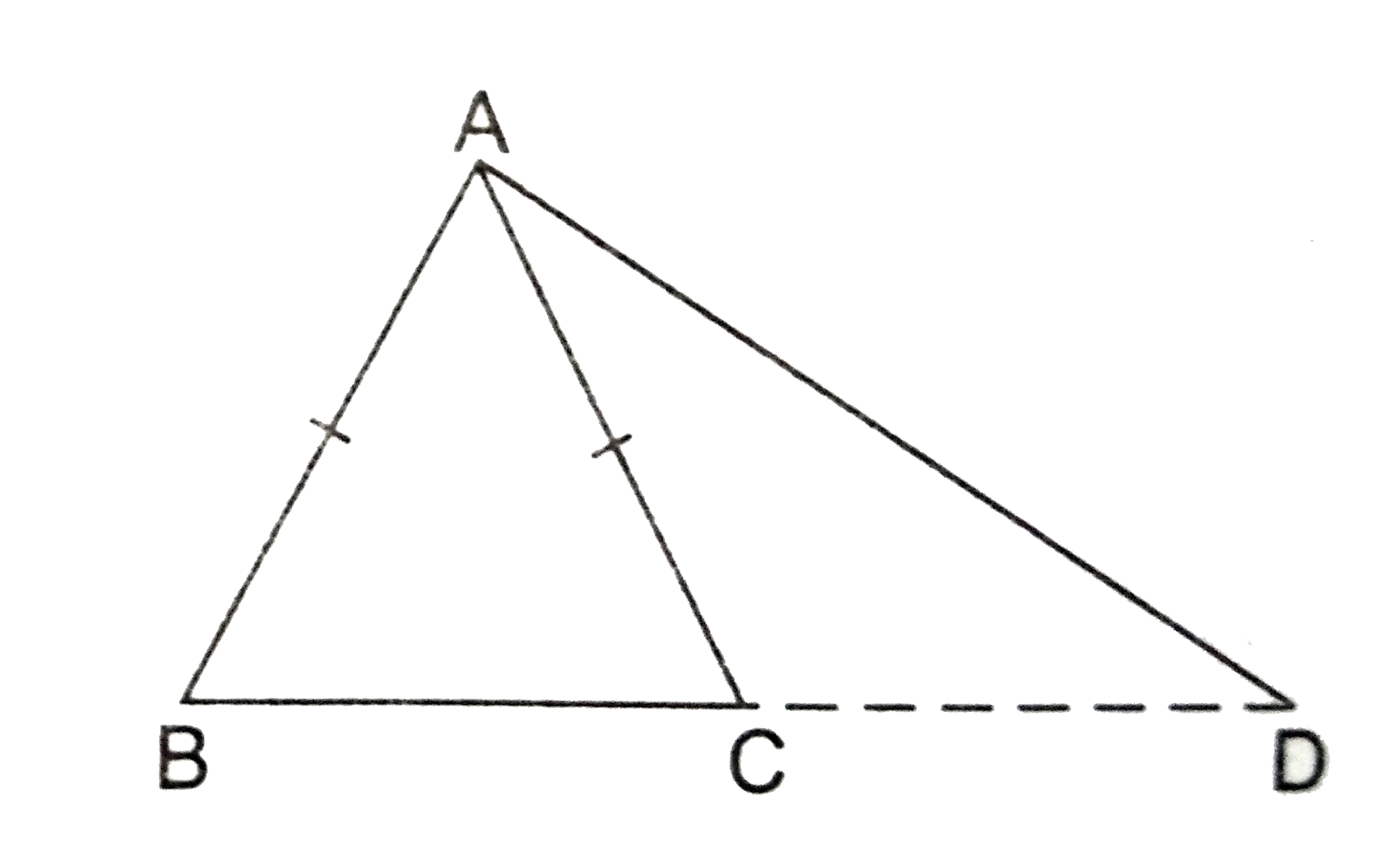
In ∆ABC AB = AC. Side BC is produced to D. Prove that AD2 - AC2 = BD. CD

Text Solution

Verified by Experts

Draw AE⊥BC meeting BC at D. Applying Pythagoras theorem in right-angled triangle AED we get:Since ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle. So BE = CE And DE+CE=DE+BE=BD

Related Solutions

In $Δ A B C, A B = A C$ . Side BC is produced to D. Prove that $(A D^{2} - A C^{2}) = B D \cdot C D$ .

View Solution
ABC is a triangle in which AB=AC and D is a point on AC such that BC^(2)=AC xx CD .Prove that BD=BC .
View Solution
ABC is a triangle in which $A B = A C and D$ is a point on AC such that $B C^{2} = A C \times C D$ .Prove that $B D = B C$ .
View Solution
ABC is a triangle with AB= AC and D is a point on AC such that $B C^{2} = A C \times C D$ . Prove that BD= BC.
View Solution
एक $△ A B C$ में, AB = AC तथा D, AC का मध्य बिंदु है और $B C^{2} = A C \times C D$ हो तो सिद्ध कीजिए कि BD = BC
View Solution
एक समद्विबाहु त्रिभुज ABC की भुजा AC पर बिंदु D इस प्रकार है की $B C^{2} = A C \times C D$ |यदि AB =AD हो तो सिद्ध करो की BD =BC
View Solution
In $A B C,$ side $A B$ is produced to $D$ so that $B D = B C \dot{}$ If $∠ B = 60^{0} a n d ∠ A = 70^{0},$ prove that: $A D > C D$ (ii) $A D > A C$

View Solution
In an isoscles $Δ A B C, A B = A C and D$ is a point on BC. Prove that $A B^{2} - A D^{2} = B D \cdot C D$ .
View Solution
ABC is a triangle in which AB = AC and D is any point on BC. Prove that:
$A B^{2} - A D^{2} = B D . C D$
View Solution
एक त्रिभुज ABC है | जिसमे AB = AC तथा D, BC पर कोई बिंदु है | तो सिद्ध कीजिए कि
$A B^{2} - A D^{2} = B D \cdot C D$
View Solution
माना एक $△ A B C$ है जिसमे AB = AC तथा AC पर एक बिंदु D है और $B C^{2} = A C \times C D$ तो सिद्ध कीजिए कि BD = BC

View Solution
If D is such a point on the side BC of $△ A B C$ that AB/AC=BD/CD, then AD must be a/an :
View Solution
आकृति में त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि $\frac{B D}{C D} = \frac{A B}{A C}$ है । सिद्ध कीजिए कि AD , कोण BAC का समद्विभाजन है ।

View Solution
The side BC of triangles ABC is produced to D so that CD = AC . If the angle BAD $= 109^{\circ} and$ the ACB $= 72^{\circ}$ prove that BD is greater than AD.
View Solution
In the given figure, D is a point on side BC of $Δ A B C$ such that $\frac{B D}{C D} = \frac{A B}{A C}$ . Prove that AD is the bisector of $∠ B A C$ .

View Solution
In fig., D is a point on side BC of $△ A B C$ such that $\frac{B D}{D C} = \frac{A B}{A C}$ . Prove that, AD is bisector of $∠ B A C$ .
.
View Solution
In Fig .D is a point on side BC of $Δ A B C$ such that $\frac{B D}{C D} = \frac{A B}{A C}$ prove that AD is the bisector of $∠ B A C .$

View Solution
एक समद्विबाहु $Δ A B C$ में $∠ A$ न्यूनकोण है, जिसमें $A B = A C$ तथा $B D ⊥ A C$ तो , सिद्ध कीजिए कि ${(B C)}^{2} = 2 A C . C D$
View Solution
In $Δ A B C$ , $B D : C D = 3 : 1$ and $A D ⊥ B C$ . Prove that $2 (A B^{2} - A C^{2}) = B C^{2}$ .
View Solution
In a $Δ A B C$ , BD is the median to the side AC, BD is produced to E such that BD = DE. Prove that : AE is parallel to BC.
View Solution

In ∆ABC AB = AC. Side BC is produced to D. Prove that AD2 - AC2 = BD. CD

Draw AE⊥BC meeting BC at D. Applying Pythagoras theorem in right-angled triangle AED we get:Since ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle. So BE = CE And DE+CE=DE+BE=BD

Related Solutions

Recommended Content