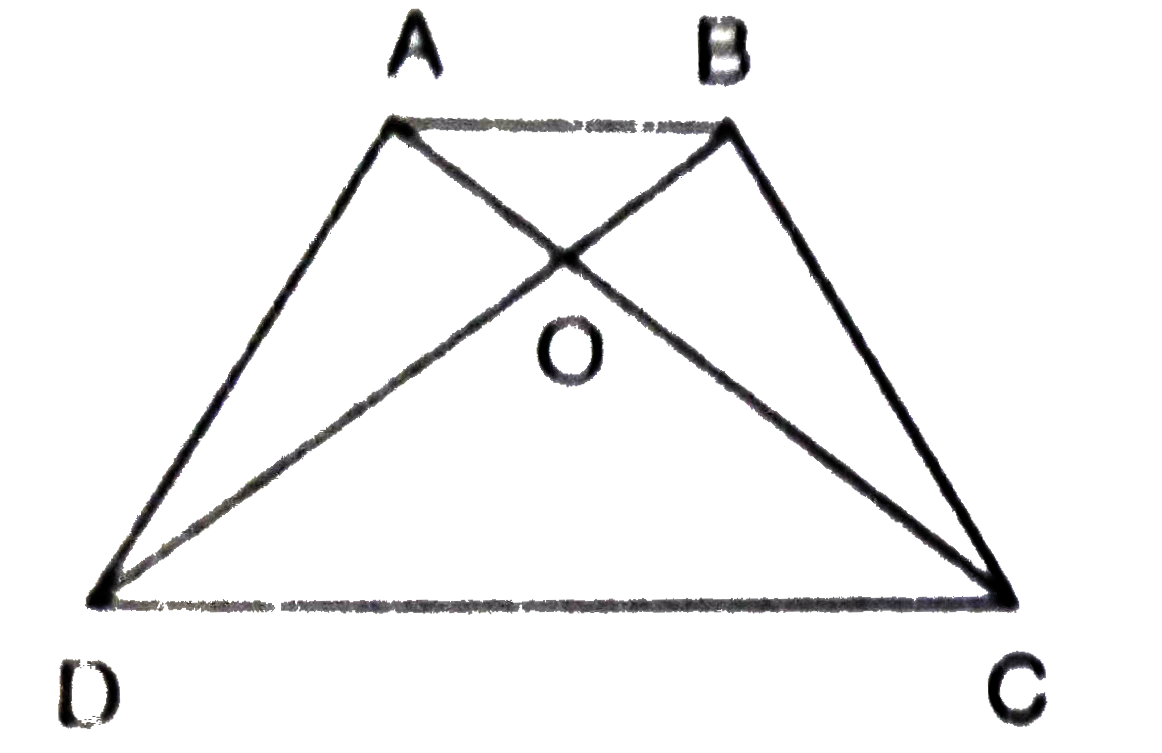
चित्र में, चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर प्रतिच्छेद इस प्रकार करते है कि OB = OD है। यदि AB = CD हो तो दर्शाइए कि
(i) ar(ΔAOD)=ar(ΔBOC)
(ii) ar(ΔABD)=ar(ΔABC)
(iii) DA ।। CB अथवा, ABCD एक समांतर चतुर्भुज है।
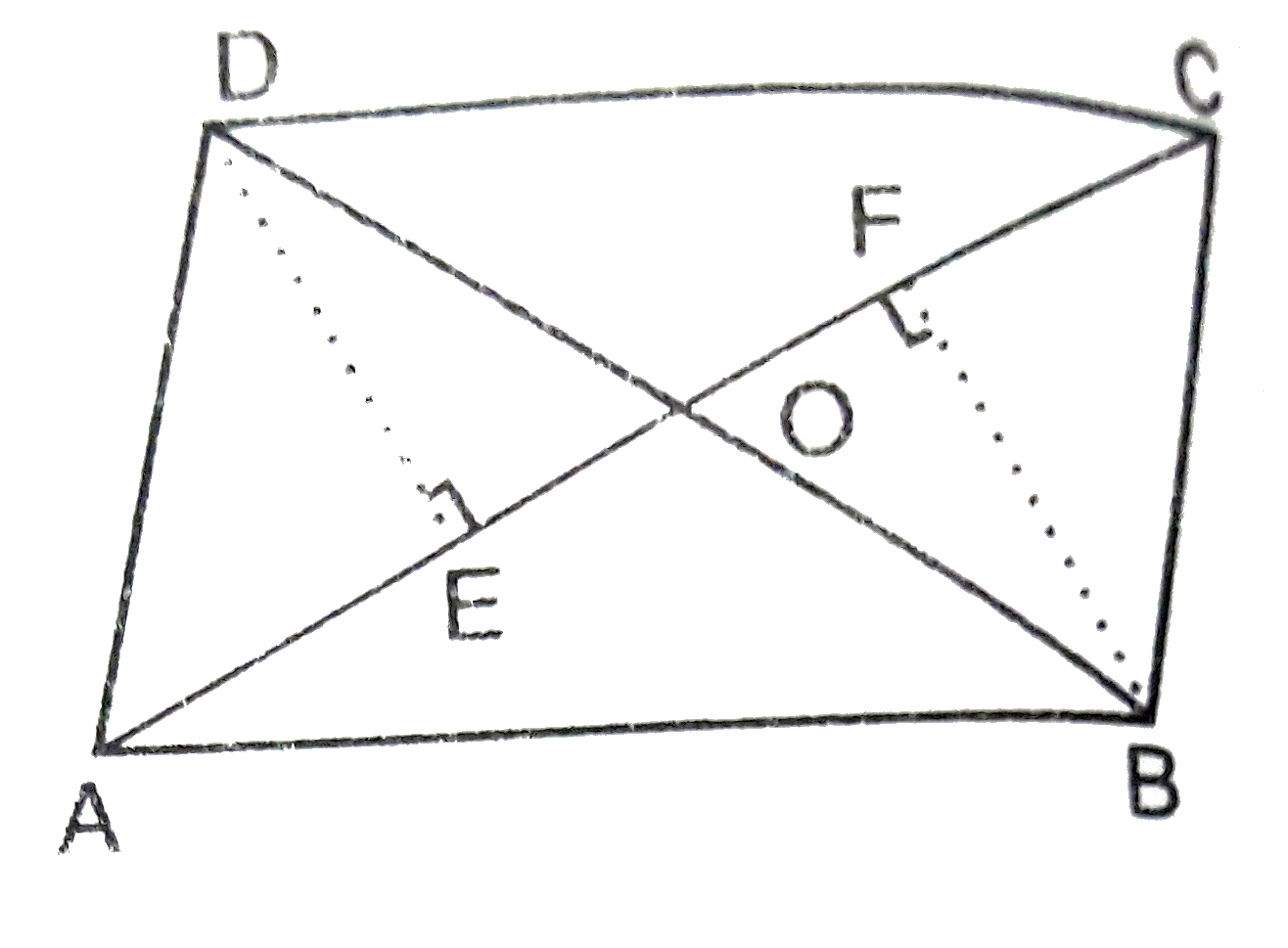
(i ) DE⊥AC तथा BF⊥AC खींचा।
त्रिभुज DOE तथा BOF में,
∠DOE=∠BOF [शीर्षाभिमुख कोण]
OD=OB
∠DEO=∠BFO
अतः कोण-कोण-भुजा सर्वांगसम अभिग्रहित से,
ΔDOE≅BOF
⇒DE=BF तथा ar(ΔDOE)=ar(ΔBOF) ...(i)
त्रिभुज AED तथा CFB पर विचार करते हैं। इन दोनों त्रिभुजों में,
AD=BC [दिया है ]
DE = BF
तथा ∠AED=∠BFC=90∘
अतः RHS सर्वांगसमता अभिग्रहित से,
ΔAED≅ΔCFB
⇒ar(ΔAED)≅ar(ΔCFB) तथा ∠DAE=∠BCF ...(ii)
(i) तथा (ii ) के संगत पक्षों को जोड़ने पर
ar(ΔDOE)+ar(ΔAED)=ar(ΔBOF)+ar(ΔCFB)
⇒ar(ΔAOD)=ar(ΔCOB)
(ii ) स्पष्ट है कि
ar(ΔAOD)=ar(ΔBOC) [(i) से ]
⇒ar(ΔAOD)+ar(ΔAOB)=ar(ΔBOC)+ar(ΔAOB)
⇒ar(ΔABD)=ar(ΔABC)
(iii ) स्पष्ट है कि
∠DAE=∠BCF [उपरोक्त (ii ) से ]
⇒∠DAC=∠BCA
⇒ AD ।। BC
अतः ABCD एक समांतर चतुर्भुज है।
∴ DA ।। CB
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:व्याख्यात्मक उदाहरण
Explore 1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
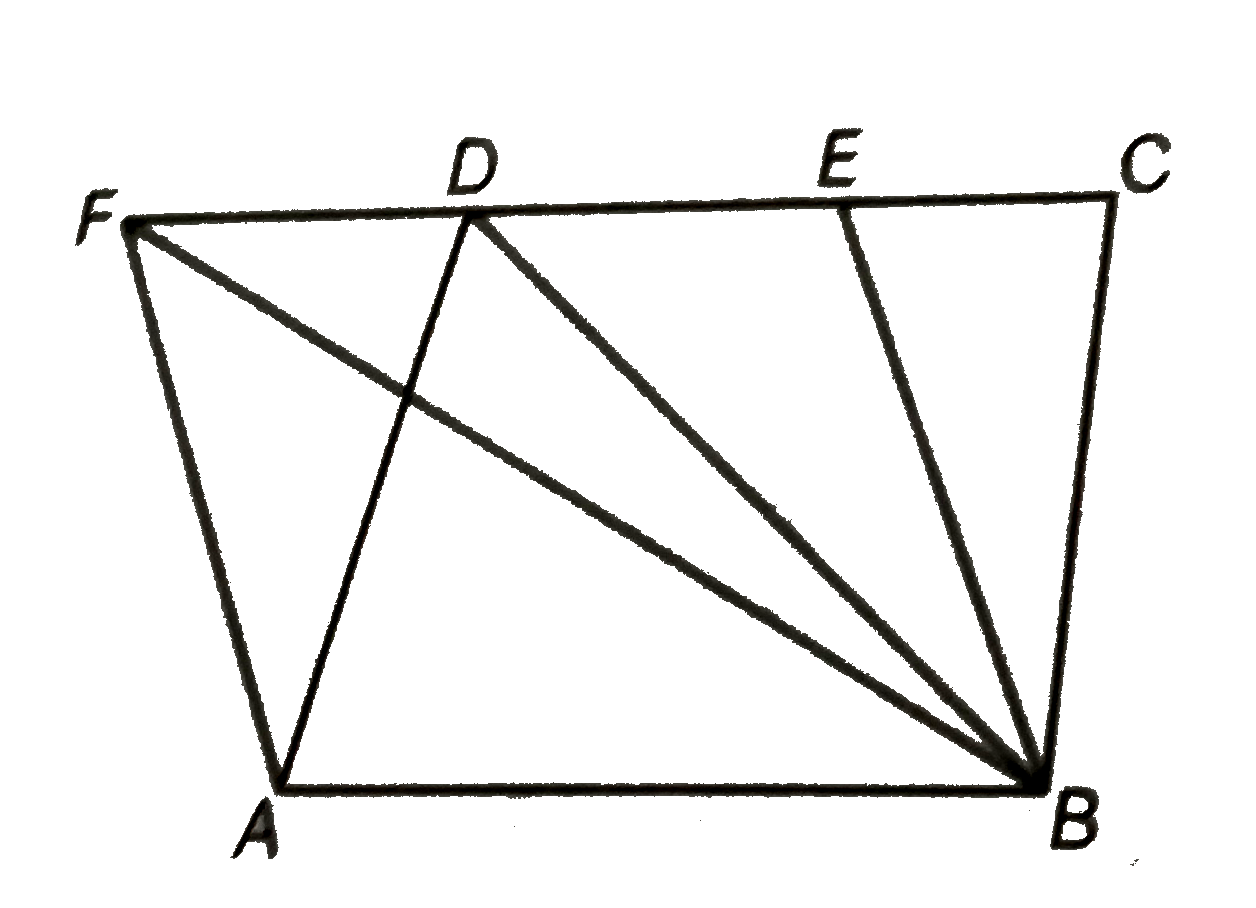
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
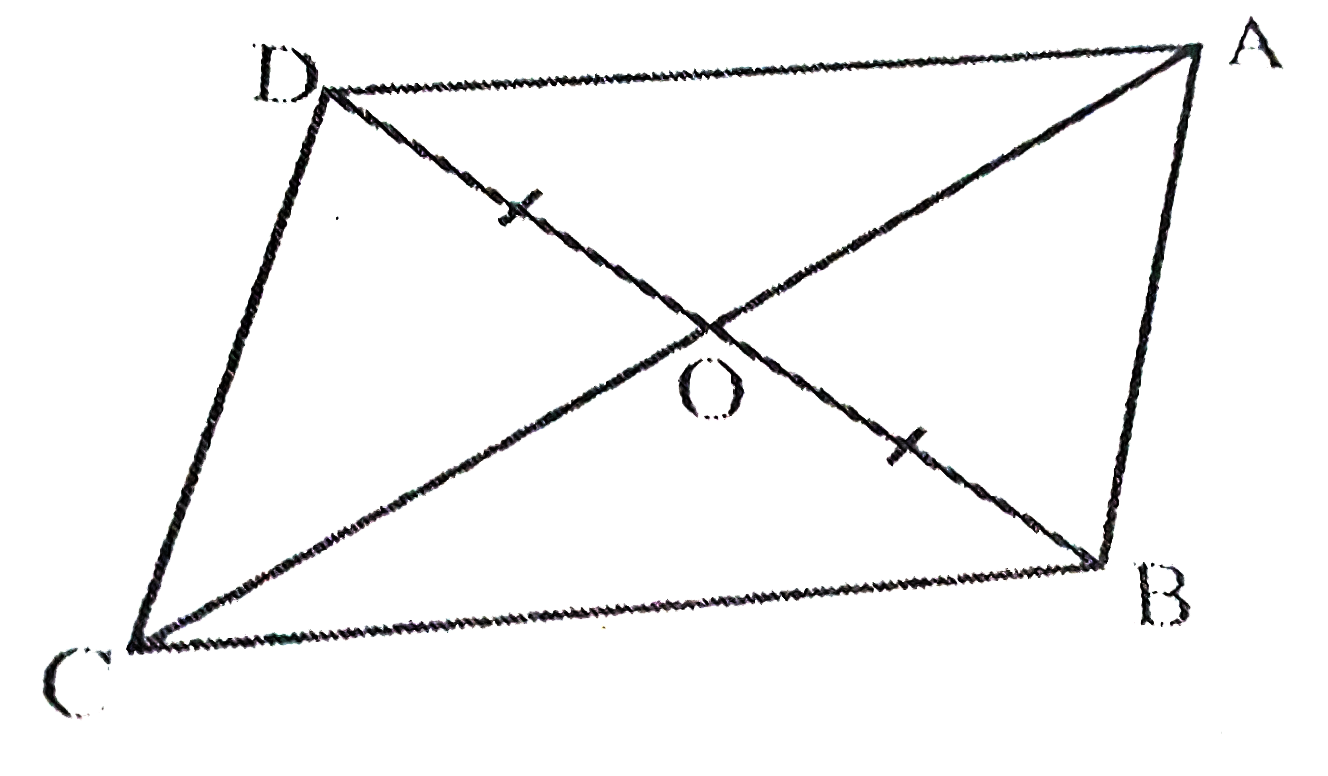
View Solutionआकृति में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB=OD है । यदि AB=CD है , तो दर्शाइए कि
(i) ar(DOC)=ar(AOB)
(ii) ar(DCB)=ar(ACB)
(iii) DA∣∣CB या ABCD एक समांतर चतुर्भुज है ।
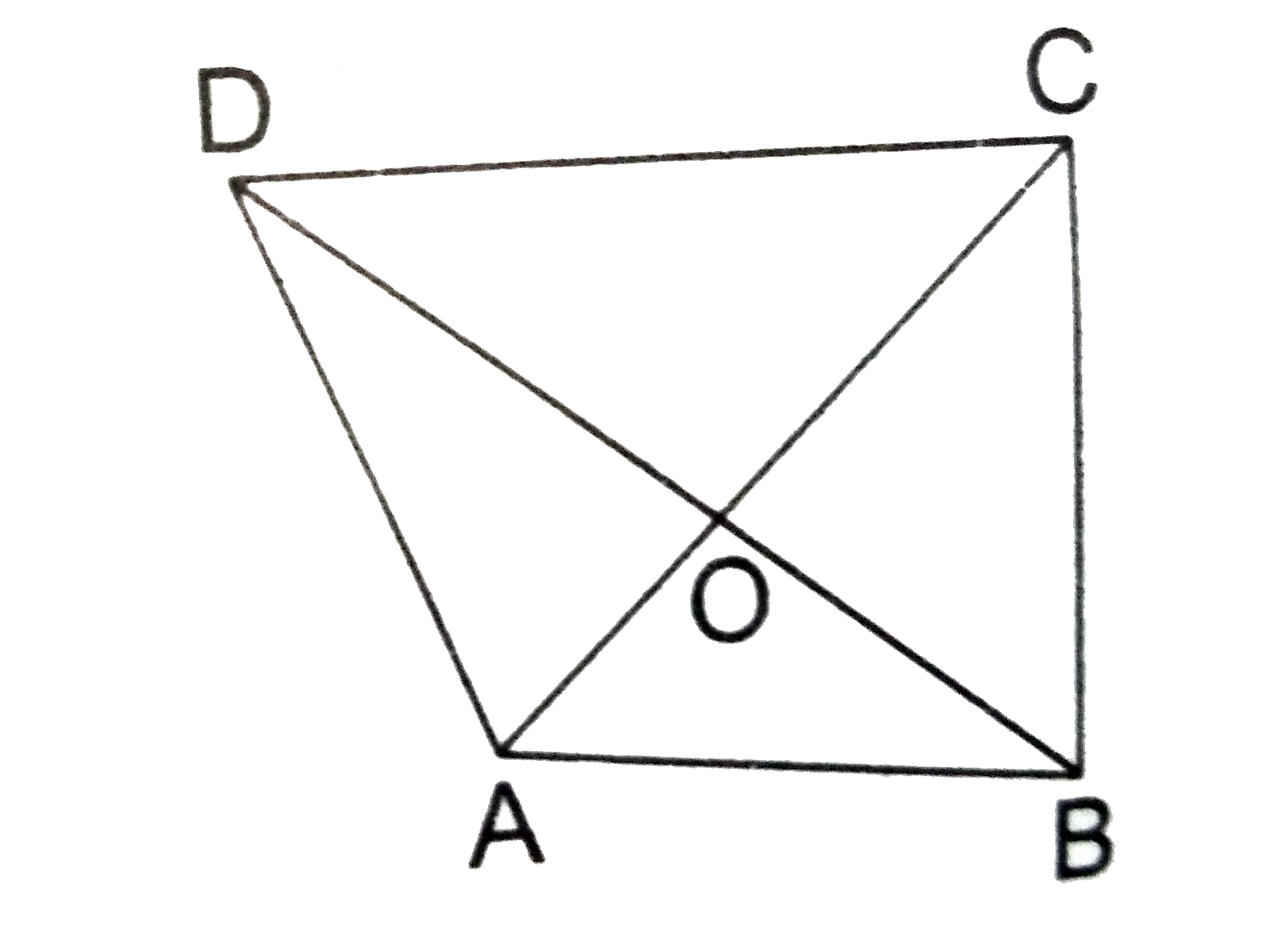
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View Solutionएक चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD)=ar(ΔBOC) है । सिद्ध करों कि ABCD एक समलम्ब है।
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View Solutionचित्र में, यदि ABCD एक समलम्ब है जिसमें AB ।। DC तो सिद्ध कीजिए कि
ar(ΔAOD)=ar(ΔBOC)
View Solutionआयत ABCD के अंदर एक बिंदु O इस प्रकार है कि ar(ΔAOD)=3 वर्ग सेमी तथा ar(ΔBOC)=6 वर्ग सेमी है, तो आयत ABCD का क्षेत्रफल होगा :
View Solutionदिए गए चित्र में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है की OB = OD है|यदि AB =CD है ,तो दर्शाइए की
(i)ar(DOC)=ar(AOB)
(ii)ar(DCB)=ar(ACB)
(iii)DA∣∣CB या ABCD एक समांतर चतुर्भुज है|
(##KCSHINMATIXC11SLV028_Q01##)
View SolutionIn the given figure, diagonals AC and BD of quadrilateral ABCD interset at O such that OB = OD. If AB = CD, then show that :
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram .
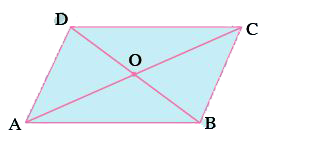
View SolutionABCD is a parallelogram. The diagonals AC and BD intersect each other at ‘O’. Prove that ar(ΔAOD)=ar(ΔBOC) . (Hint: Congruent figures have equal area)
View Solution