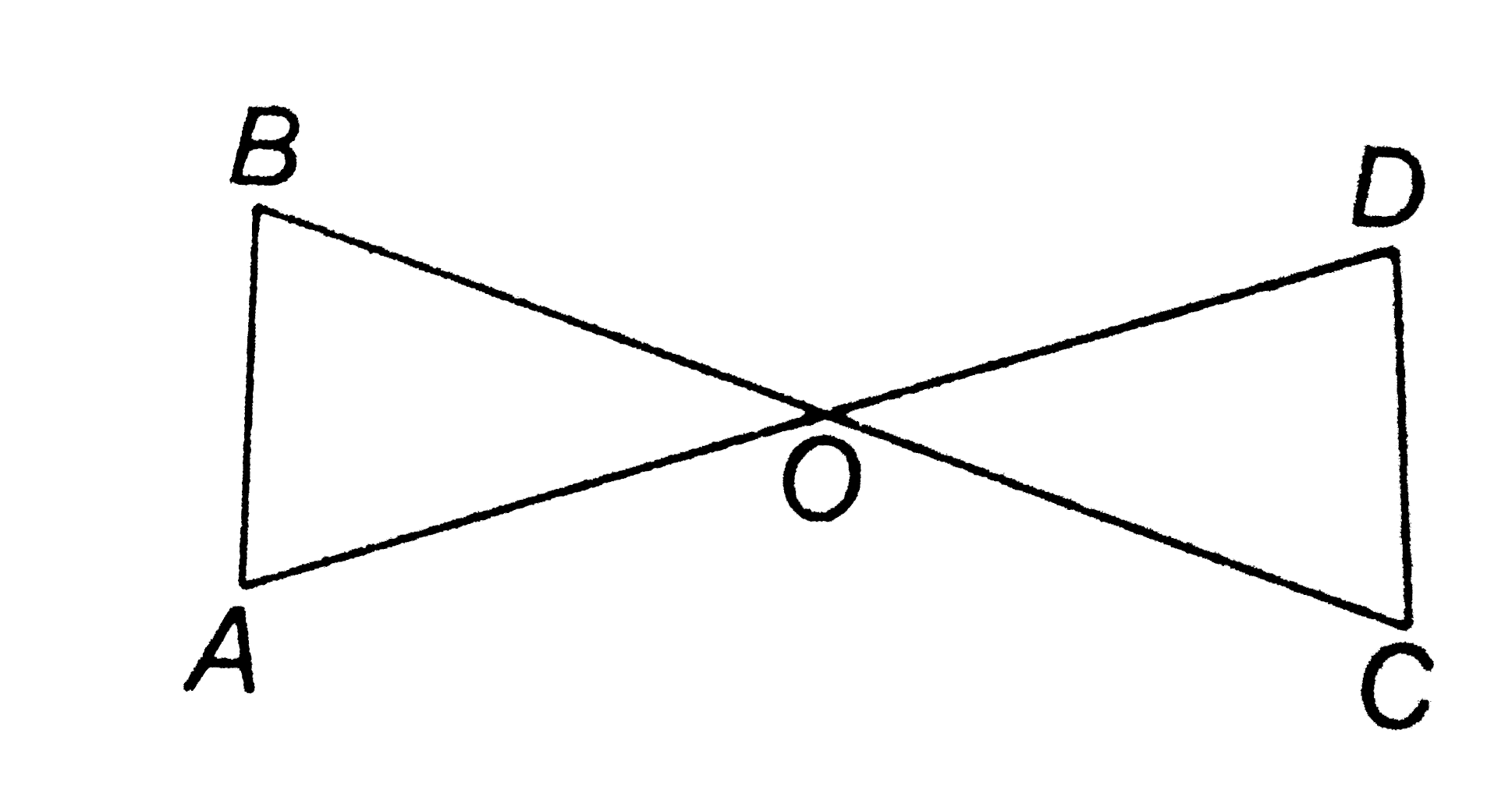
संलग्न चित्र में, AB =CD तथा AB∣∣CD है। सिद्ध कीजिए कि :
(i) ΔAOB≅ΔDOC
(ii) ACऔर BD एक-दूसरे को बिन्दु O पर समद्विभाजित करते है।
(i) ∵AB∣∣CD (दिया है)
⇒∠1=∠2 और ∠3=∠4 (एकान्तर कोण)
अब ΔAOB और ΔDOC में,
∵⎧⎪
⎪⎨⎪
⎪⎩∠1=∠2 (एकान्तर कोण)AB=DC (दिया है)∠3=∠4 (एकान्तर कोण)
अतः ΔAOB≅ΔDOC (A.S.A.)
(ii) ⇒BC,AD को समद्विभाजित करती है।(c.p.c.t)
तथा BO=CO
⇒AD,BC समद्विभाजित करते है। (c.p.c.t.)
अतः AD और BC एक-दूसरे को समद्विभाजित करते है।

Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - साधित उदाहरण
11 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7A
30 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
ΔABC में, ∠A=100∘,∠C=30∘ है। ΔABC (i) सबसे बड़ी (ii) सबसे छोटी भुजा कौन-सी है?
View Solutionनिम्नलिखित में से कौन-से त्रिभुजों के युग्म सर्वांगसम है ? प्रत्येक में सर्वागसमता का प्रतिबन्ध भी बताइए :
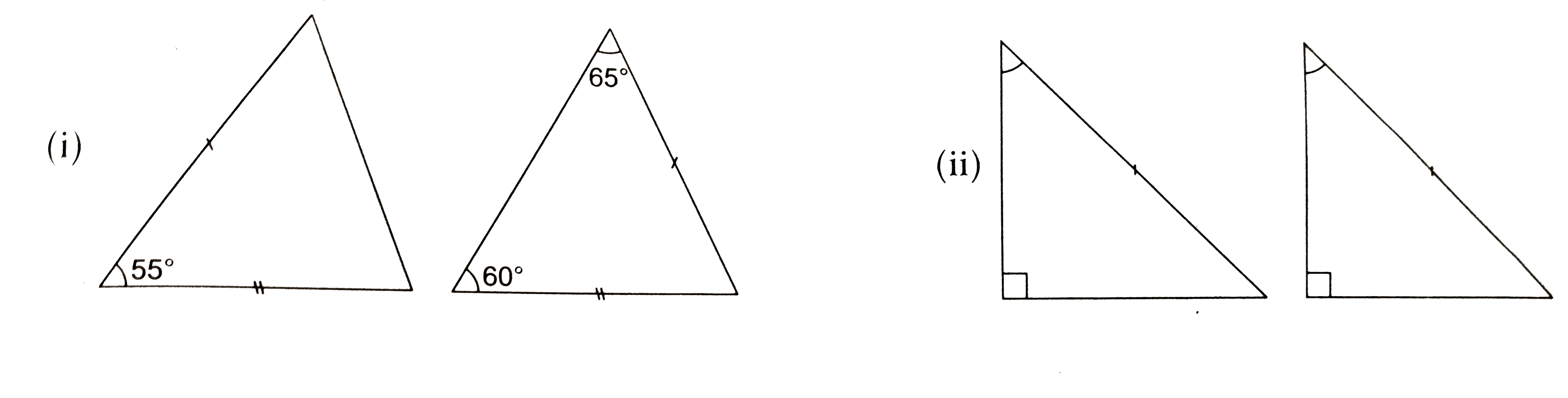
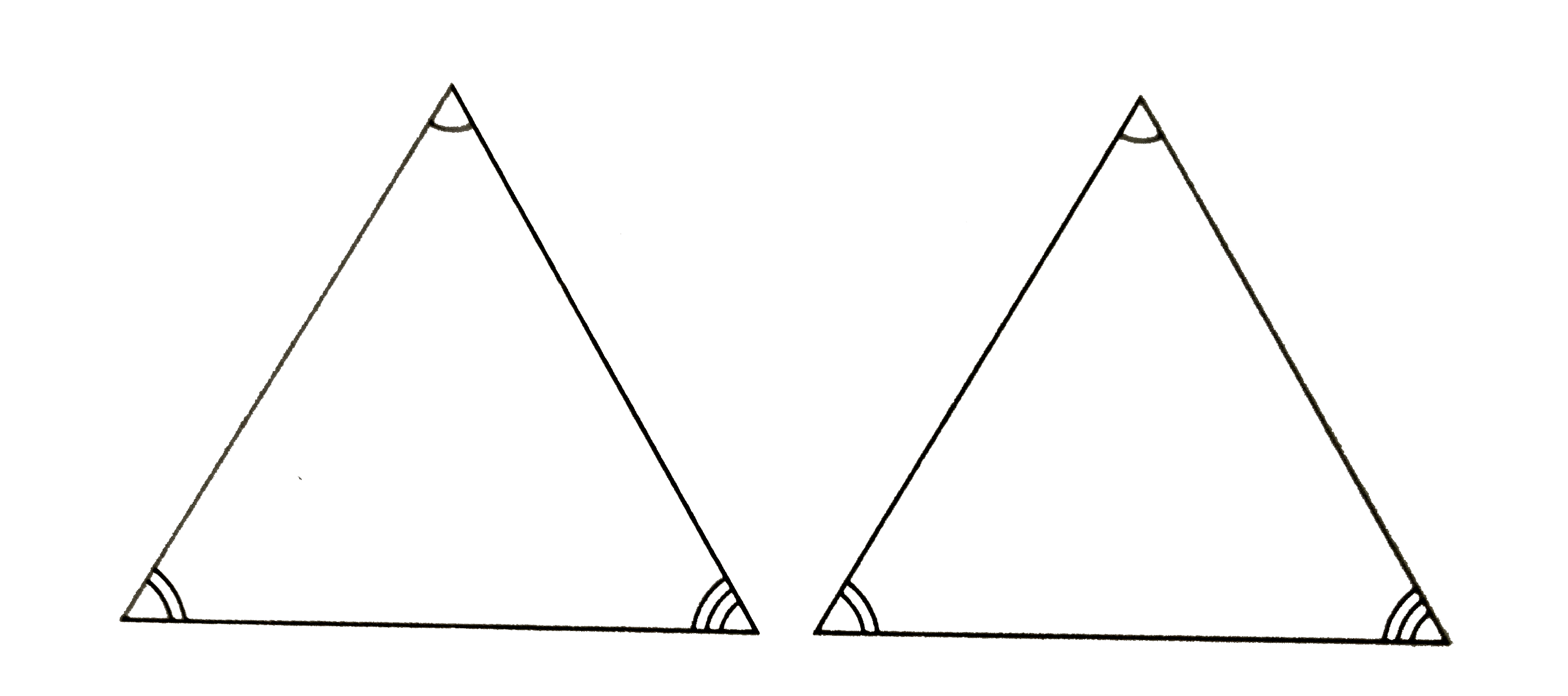
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
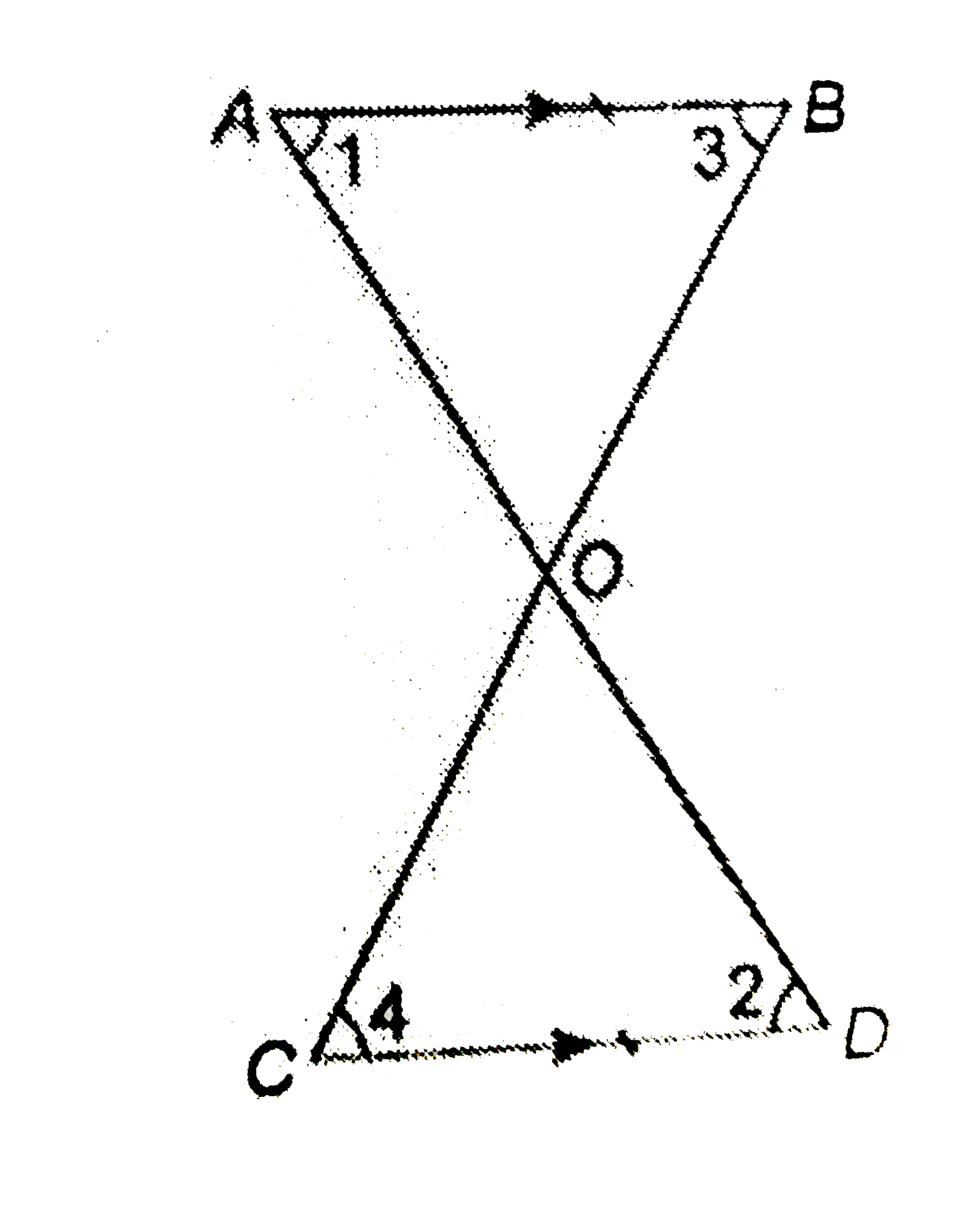
View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.
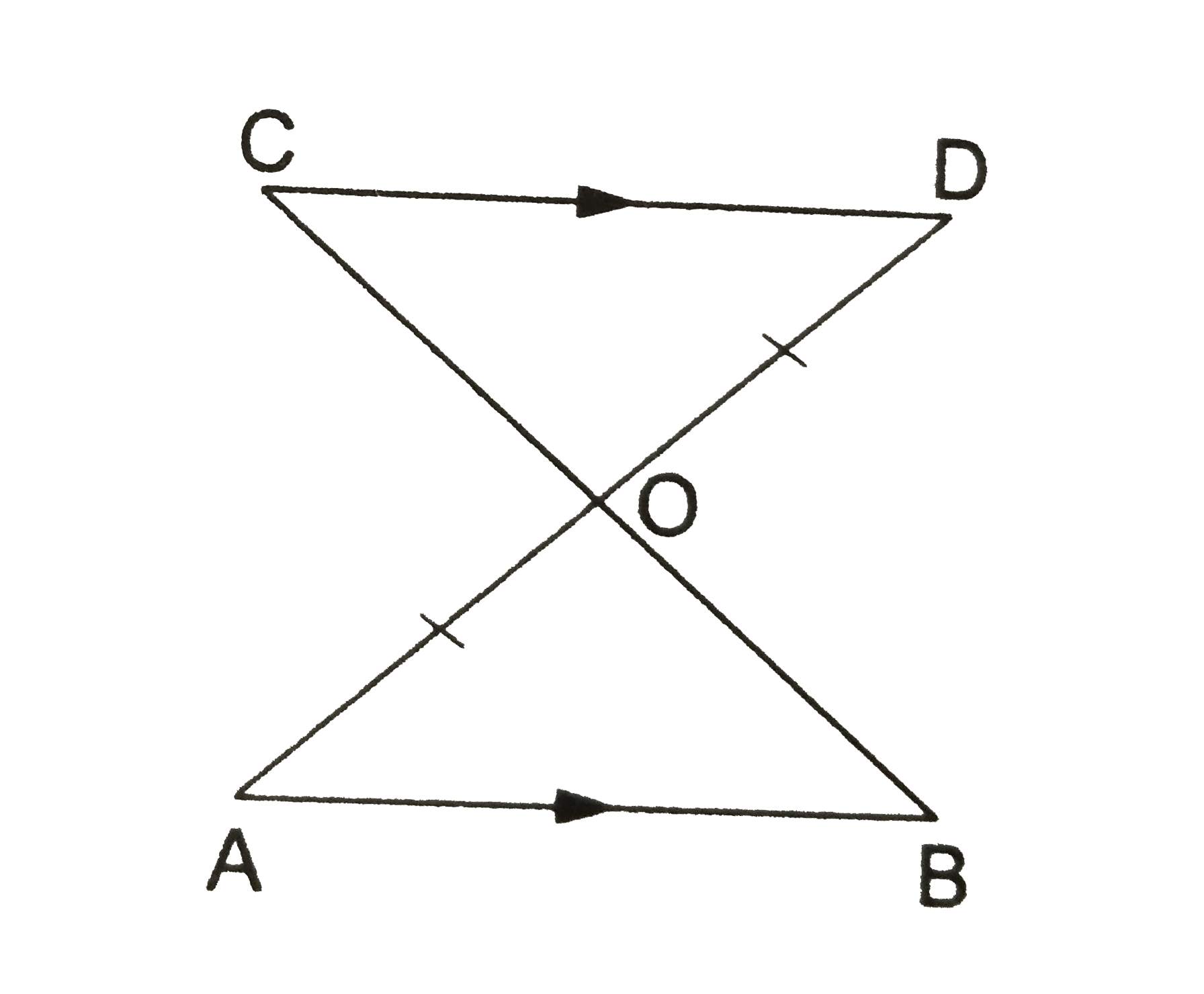
View Solutionचित्र में ΔAOB~ΔDOC , सिद्ध करें कि AB∣∣CD.
View Solutionदिए चित्र में यदि, AB||CD तो सिद्ध कीजिये कि ΔAOB~ΔDOC
View Solutionकिसी ΔOAB में ∠AOB=90∘ तथा बिन्दु P, Q भुजा AB को समत्रिभाजित करते हैं | सिद्ध कीजिए कि, OP2+OQ2=59AB2.
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionसिद्ध कीजिए कि बिन्दु (2,0),(11,6) तथा (−4,−4) समरेख है।
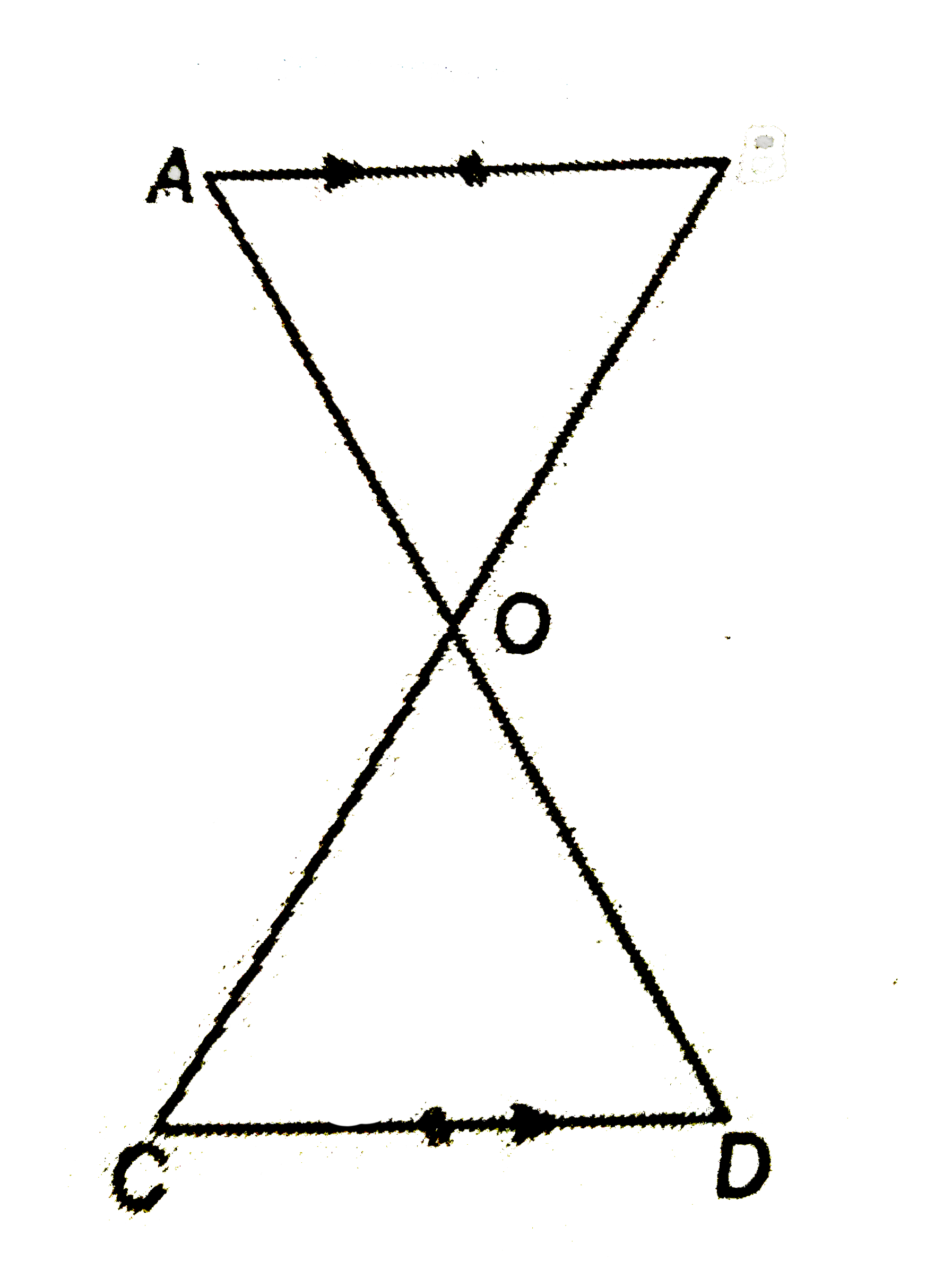
View SolutionIn the given figure, AB∣∣CD and AB=CD, prove that: ΔAOB≅ΔDOC

View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.

View SolutionIn the adjoining figure AB=CD and AB||CD prove that :
(i) ΔAOB≅ΔDOG
(ii) AD and BC bisect each other at point O.
View Solution
