यदि ABCD एक चतुर्भुज हों, तो सिद्ध कीजिए कि-
(i) AB + BC + CD + DA > 2AC
(ii) AB + BC + CD + DA > AC + BD
The correct Answer is:ΔABC ~-= ΔDEF
Topper's Solved these Questions
- त्रिभुज BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.1
7 Videos
- त्रिभुज BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.2
8 Videos
- चतुर्भुज BOOK - SCIENCE PUBLICATIONCHAPTER - चतुर्भुज EXERCISE - प्रश्नावली 8.2 पर आधारित अभ्यास प्रश्न
7 Videos
- दो चरों वाले रैखिक समीकरणBOOK - SCIENCE PUBLICATIONCHAPTER - दो चरों वाले रैखिक समीकरणEXERCISE - प्रश्नावली 4.4 पर आधारित अभ्यास प्रश्न
1 Videos
Similar Questions
चतुर्भुज ACBD में, AC -= AD है और AB कोण A को सम्द्धिभाजिक कहेते है (देखिए आकृति) | दर्शाइए कि ∠ABC -= ∠ABD है |
BC और BD के बारे में आप क्या कह सकते है ?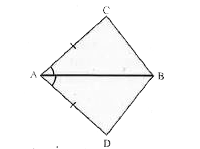
View Solutionएक समद्धिबाहू त्रिभुज ABC में जिसमे AB -= AC है, ∠B और ∠C के समद्धिभाजक परस्पर बिन्दु O पर प्रतिच्छेद करते है | A और O को जोडिए | दर्शाइए कि
(i) OB -= OC
(ii) AO कोण A को समद्धिभाजित करता है |
View SolutionP, Q और R क्रमशः एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु है। सिद्ध कीजिए कि ΔPQR भी एक समबाहु त्रिभुज हैं।
View Solutionनिम्नलिखित समीकरणों को (i) संख्या रेखा और तथा (ii) कार्तिए तल पर प्रदर्शित कीजिए।
(a) x−2=0 " (b)2x+4=3x+1
(c) y+5=0
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).
View SolutionIn a quadrilateral ABCD, show that (AB+BC+CD+DA)<2(BD+AC).
View Solutionदिखाइये कि एक चतुर्भुज ABCD में AB+BC+CD+DA>AC+BD
View Solutionयदि ABCD एक चतुर्भुर्ज है जिसके विकर्ण AC और BD,O पर परिच्छेद करते है तो सिद्ध कीजिए की :
(i)(AB+BC+CD+DA)>(AC+BD)
(ii) (AB+BC+CD+DA)<2(AC+BD)

View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionABCD ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ। ਕੀ AB+BC+CD+DA>AC+BD ?
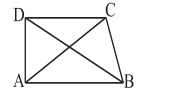
View Solution
