Four point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.
The correct Answer is:A, C, D
To solve the problem step by step, we will analyze the forces acting on the charged particle and derive the necessary equations to find the least value of its initial velocity v0 and the kinetic energy at the origin.
Step 1: Understanding the Configuration
We have four point charges:
- +8μC at y=√272
- −1μC at y=−√32
- −1μC at y=√32
- +8μC at y=−√272
The particle of mass m=6×10−4kg and charge q=+0.1μC moves along the x-direction.
Step 2: Finding the Electric Field at the Null Point
To find the least value of v0, we need to determine the electric field at the position where the net electric field is zero (the null point). The electric field due to a point charge is given by:
E=k|q|r2
where k is Coulomb's constant.
Step 3: Setting Up the Equation for Null Point
The electric field due to the +8μC charges will be directed away from the charges, while the field due to the −1μC charges will be directed towards them.
Let x be the distance from the origin to the null point. The electric field due to the +8μC charge at y=√272 is:
E+8=k8×10−6(x2+272)
The electric field due to one −1μC charge at y=−√32 is:
E−1=k1×10−6(x2+32)
Setting the magnitudes equal for the null point:
2E+8=E−1
Step 4: Solving for x
Substituting the expressions for the electric fields:
2⎛⎝k8×10−6(x2+272)⎞⎠=k1×10−6(x2+32)
Cancelling k and simplifying gives:
16×10−6(x2+32)=1×10−6(x2+272)
Step 5: Rearranging and Solving the Equation
Rearranging and simplifying leads to:
16(x2+32)=x2+272
15x2=16×32−272
15x2=24−13.5=10.5
x2=10.515=710
Thus,
x=√710=√7010
Step 6: Finding the Electric Field at the Null Point
Now, we can find the electric field at this point:
E=k8×10−6(x2+272)
Step 7: Work Done by Electric Field
The work done by the electric field when the particle moves from infinity to the null point is equal to the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial=12mv20−0
Step 8: Equating Work Done to Electric Potential Energy
The work done can also be expressed in terms of electric potential energy:
W=qV
Where V is the potential at the null point.
Step 9: Finding v0
Setting the two expressions for work done equal gives:
12mv20=qV
Solving for v0:
v0=√2qVm
Step 10: Kinetic Energy at the Origin
The kinetic energy at the origin can be calculated using:
KE=12mv2
Final Results
After substituting the values and solving, we find:
1. The least value of v0 is 3m/s.
2. The kinetic energy at the origin is 2.6×10−4J.
We have four point charges:
- +8μC at y=√272
- −1μC at y=−√32
- −1μC at y=√32
- +8μC at y=−√272
To find the least value of v0, we need to determine the electric field at the position where the net electric field is zero (the null point). The electric field due to a point charge is given by:
The electric field due to the +8μC charges will be directed away from the charges, while the field due to the −1μC charges will be directed towards them.
Substituting the expressions for the electric fields:
Rearranging and simplifying leads to:
Now, we can find the electric field at this point:
The work done by the electric field when the particle moves from infinity to the null point is equal to the change in kinetic energy:
The work done can also be expressed in terms of electric potential energy:
Setting the two expressions for work done equal gives:
The kinetic energy at the origin can be calculated using:
After substituting the values and solving, we find:
2. The kinetic energy at the origin is 2.6×10−4J.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Electric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
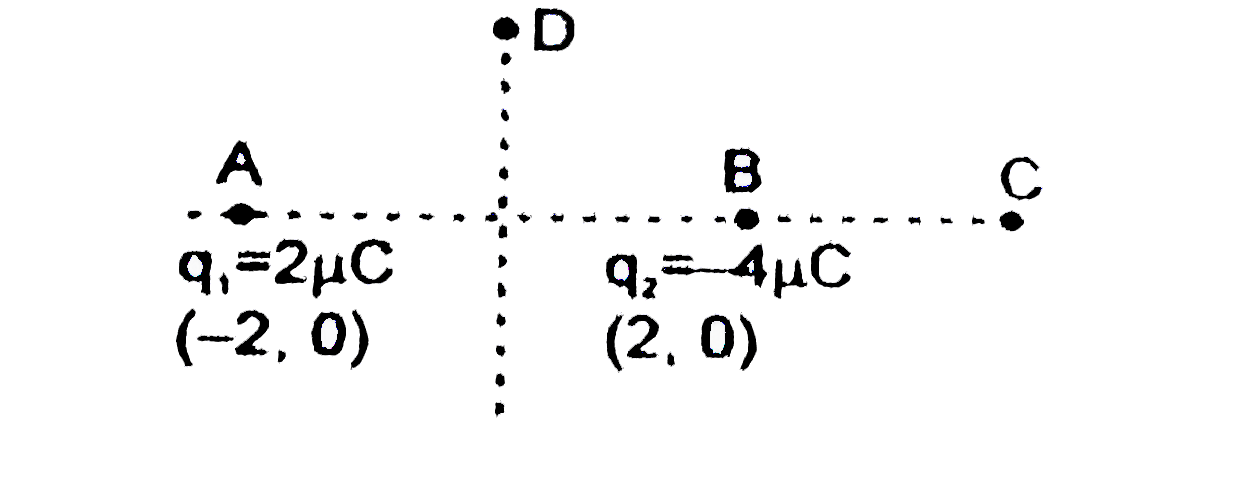 View Solution
View SolutionTwo point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
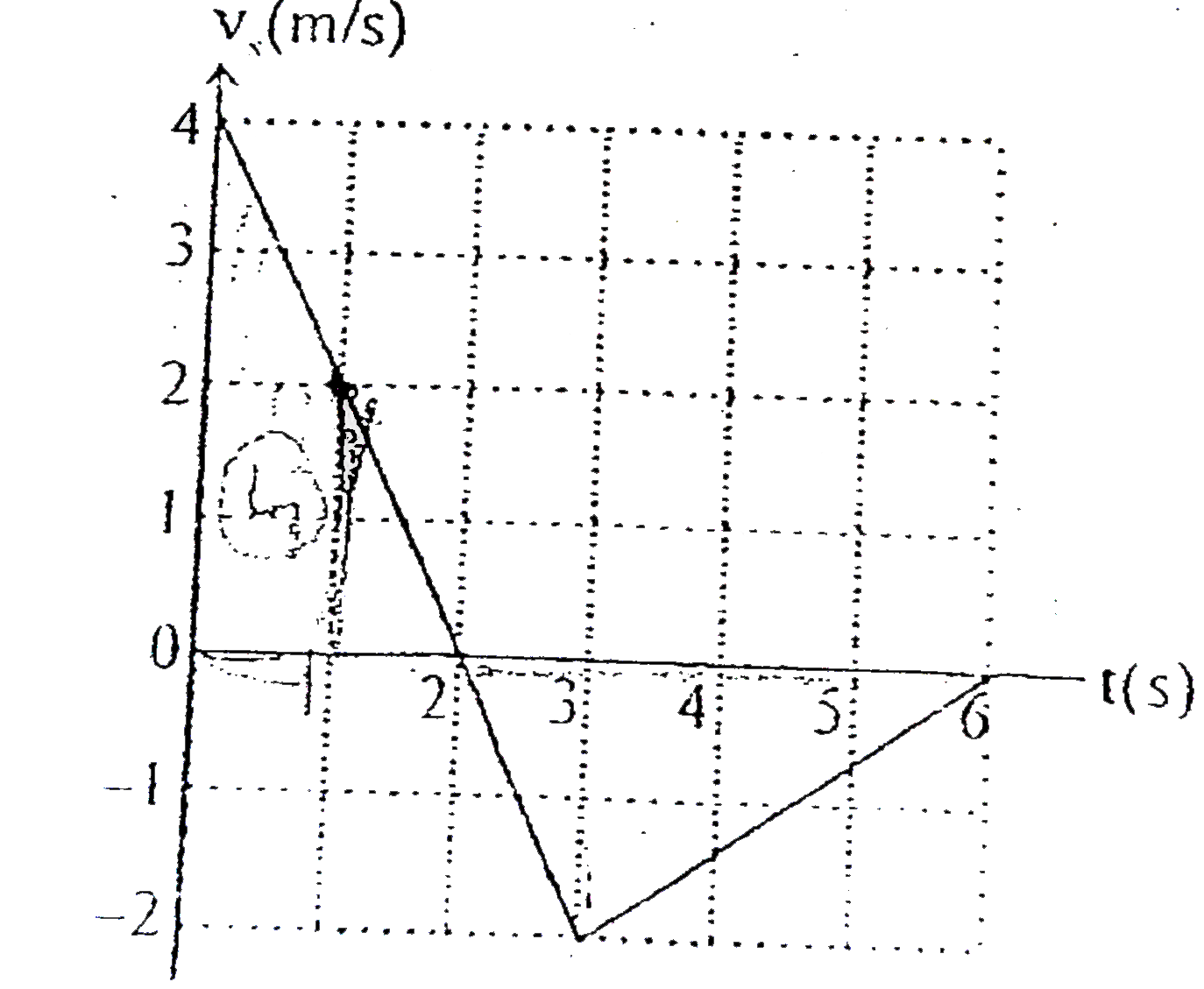 View Solution
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
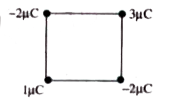
View SolutionFour point charges 1μC,3μC,−2μCand−2μC are arranged on the four vertices of a square of side 1 cm. The dipole moment of this charge assembly is
 View Solution
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View Solution

