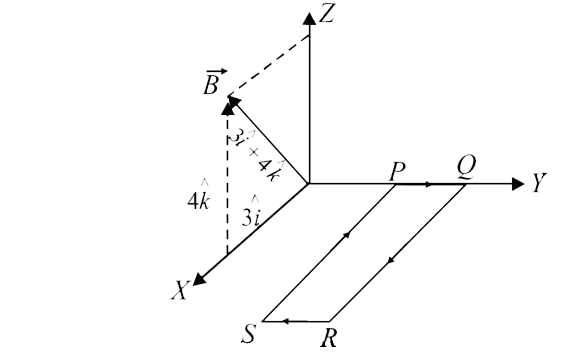
A rectangular loop PQRS made from a uniform wire has length a, width b and mass m. It is free to rotate about the arm PQ, which remains hinged along a horizontal line taken as the y-axis (see figure). Take the vertically upward direction as the z-axis. A uniform magnetic field →B=(3ˆi+4ˆk)B0 exists in the region. The loop is held in the x-y plane and a current I is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium

(a) What is the direction of the current I in PQ?
(b) Find the magnetic force on the arm RS.
(c) Find the expression for I in terms of B0, a, b and m
The correct Answer is:A, B, C, D
Let us consider the current in the clockwise direction in loop PQRS. Force on wire QR.
−−→FQR=I(→l×→B)=I[(aˆi)×(3ˆi4ˆk)(B0]
=I(B0)[3aˆi׈i×4aˆi׈k)=I(B0)[0+4a(−ˆj)]=−4a(B0)I(ˆj)
Force on wire PS
−−→FPS=I(→l×→B)=I[a(−ˆi)×(3ˆi+4ˆk)B0]=4aB0I(ˆj)
Thus we see that force on QR is equal and opposite to htat on PS and balance each other.
The force on RS is
−−→FRS=I(→l×→B)=I[b(−ˆj)×(3ˆi+4ˆk)B0]
=IbB0[3ˆk−4ˆi] ...(i) and The torque about PQ by this force is
−−→τRS=→r×→F=(ˆia)×(3ˆk−4ˆi)IbB0
IabB0(3ˆj)...(ii)
The torque about PQ due to weight of hte wire PQRS is
(τ)=mg(a2) ...(iii)
For the wire loop to be horizontal we have to equate (ii) and (iii) 3IabB0=mg(a2)
⇒I+mg6bb0 ...(iv)
Therefore,
(a) The direction of current assumed is right. This is because torque due to mg and current are in opposite directions. Therefore, current is from p to Q.
(b) from (i), −−→FRS=IbB0(3ˆk−4ˆi)
(c ) from (iv) I=mg6aB0.
Topper's Solved these Questions
Similar Questions
A rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
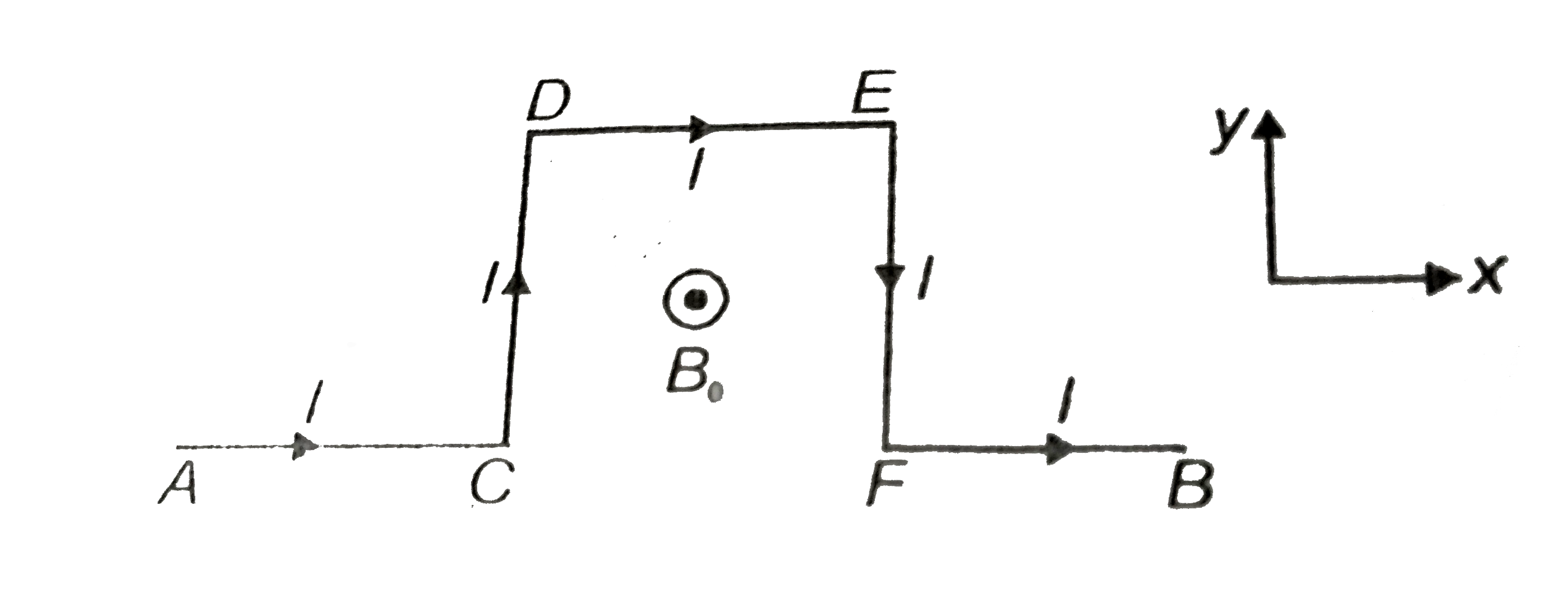
View SolutionA uniform magnetic field →B=B0ˆk exists in a region. A current carrying wire is placed in x-y plane as show. Find the force acting on the wire AB, if each section of the wire is of length 'a'.
View Solution
Knowledge Check
A conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
AzeroB2B0lv0CB0lv0D√2B0lv0A uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
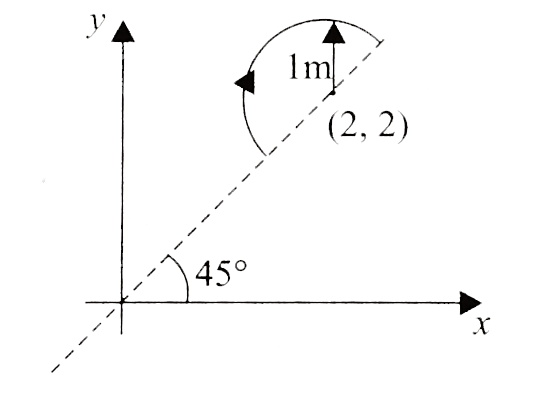 A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)
A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)In the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is
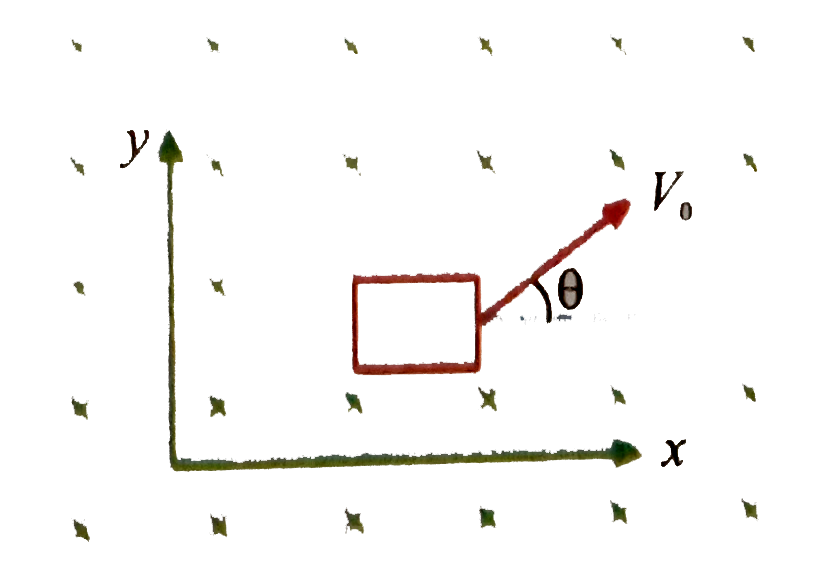 AzeroBAlong +x directionCalong −x directionDalong +y direction
AzeroBAlong +x directionCalong −x directionDalong +y direction
A thin conducting rod of length l=5m is moved such that its end B moves along the X-axis while end A moves along the Y-axis A uniform magnetic field B=6ˆk T exists

View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
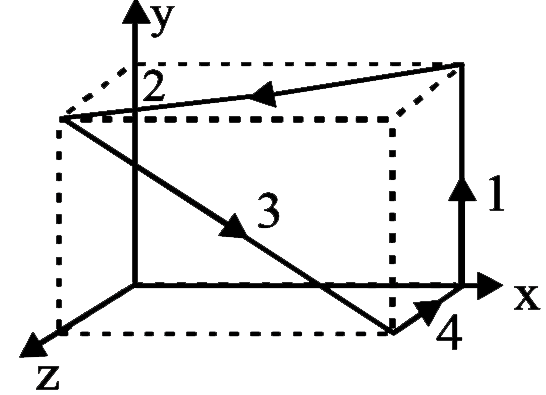
The net force on the loop
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
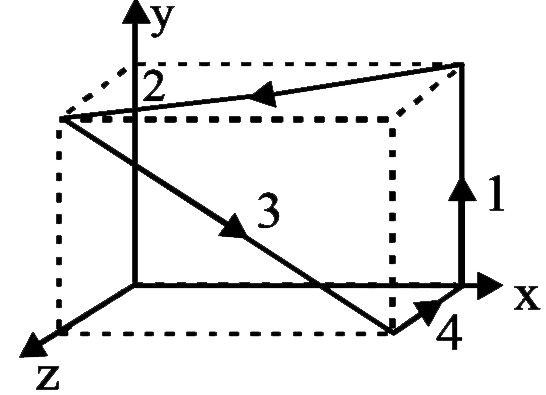
The net torque on the loop
View SolutionA dipole of magnetic moment →m=30ˆjAm2 is placed along the y-axis in a uniform magnetic field →B=(2ˆi+5ˆj)T. The torque acting on it is
View SolutionA charge q moves with a velocity 2ms−1 along x-axis in a uniform magnetic field →B=(ˆi+2ˆj+3ˆk) then charge will experience a force
View Solution
