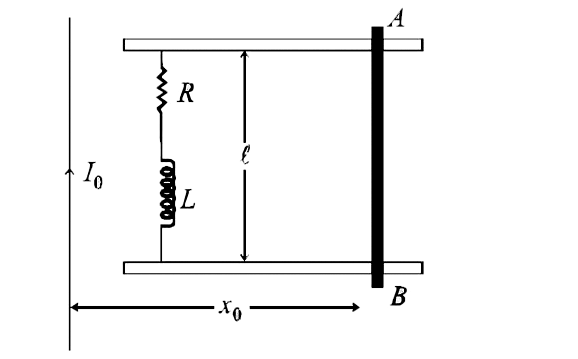
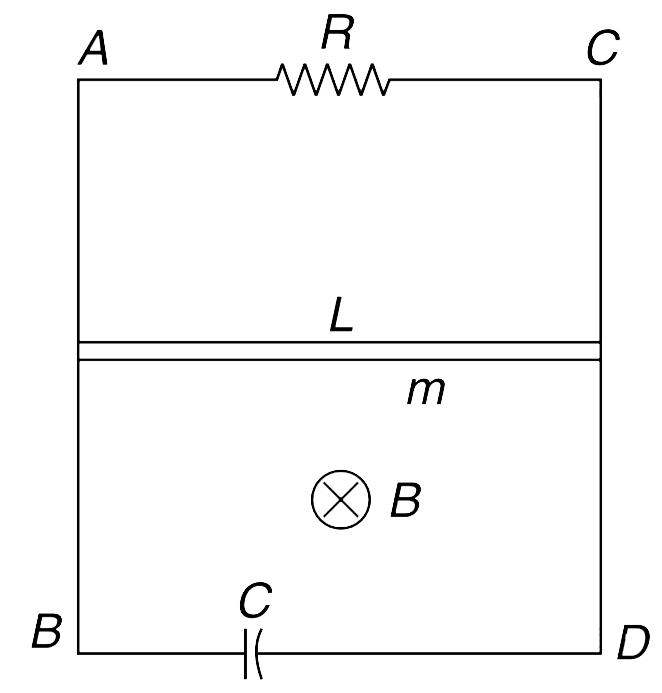
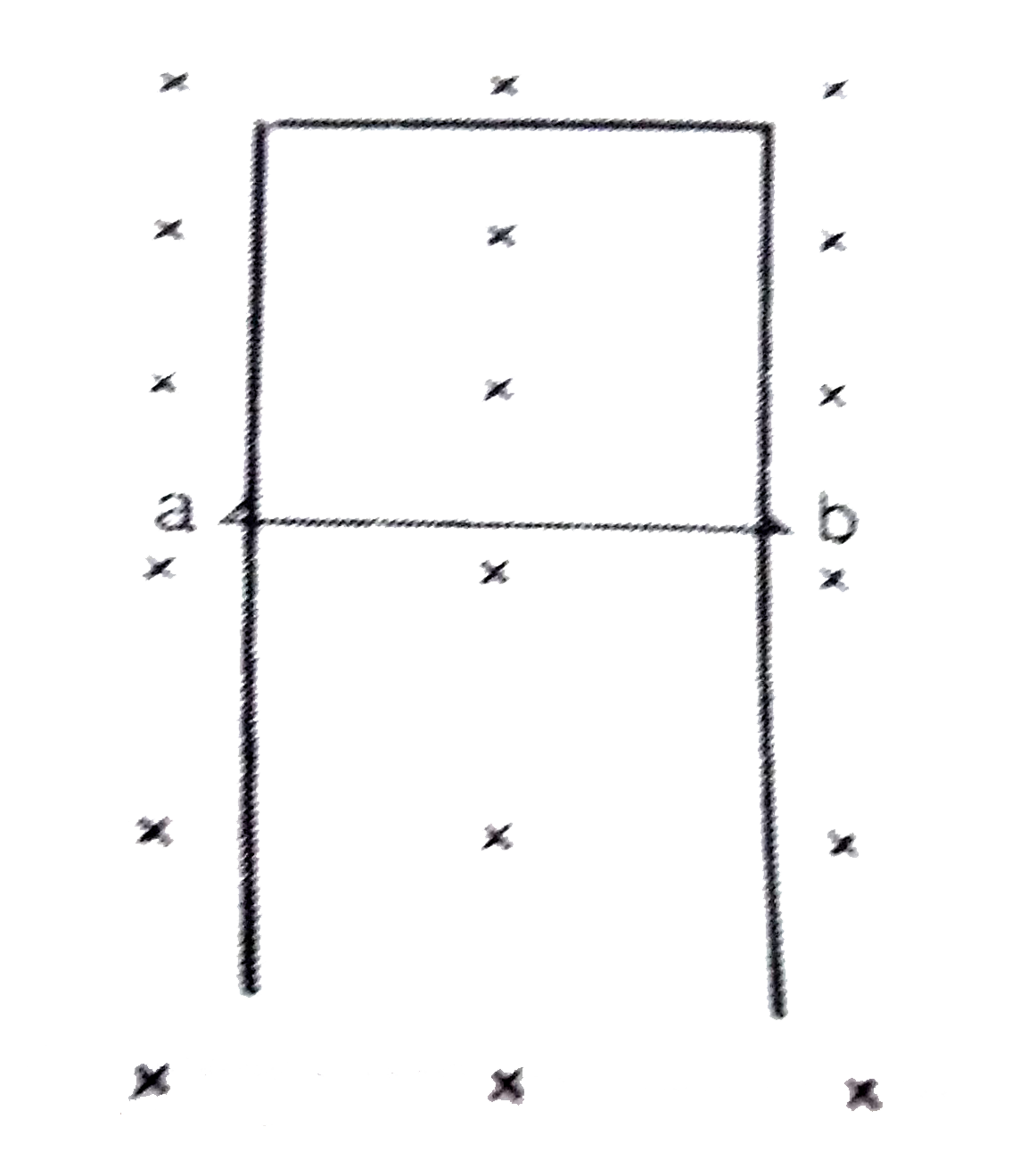
A metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
The correct Answer is:A, B, C, D
As the metal bar AB moves towards the right the magnetic flux in the loop. ABCD increases in the downward direction. By Lenz's law, to oppose this current will flow inanticlock wise direction as shown in figure.
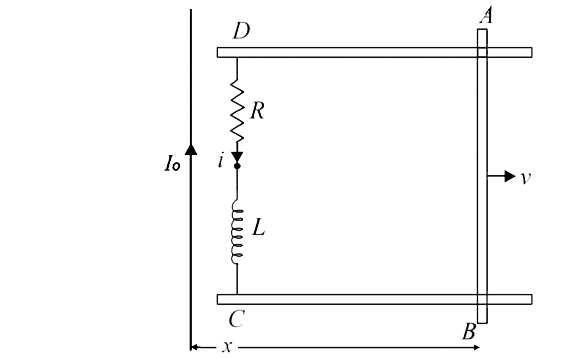 Applying Kirchhoff's loop law in ABCD, we get
Applying Kirchhoff's loop law in ABCD, we get
dϕdt=iR+Ldidt( ...(i)(b) Let AB beat a distance x fro the long striaght wire at any instant of time t during its mition, The magnetic field at that instant at AB due to lang striaght current carrying wire is
B=μ0I02πx)
The change in flux through ABCD in time dt is
(dϕ)=B(dA)=Bldx
Therefore, the total flux change when metal bar moves from a distance (x0)→2(x0) is
(Δϕ)=∫2x0x0Bldx=l∫2x0x0μ0I02πdx=μ0I0l2π[logex]2x0x0
=μ0I0l2πloge2 ....(ii) THe charge flowing through resistance R in time T is
q=∫T0∫T0[E∈duced−Ldidt]dt(omeq.(i))<br>=1/R int_(0)^(T) E_(induced) dt -L/R int _(0)^(l_1) d i=1/R (Delta phi)-L/R(i_1)<br>q=1R[μ0I0l2πloge2]−LR(i1)omeq(ii)
(c) When the metal bar AB is stopped, the rate of change of magnetic flu through ABCD bexomes zero. from (i),
iR=−Ldidt
∫2TTdt=LR∫i1/4i1dii
T==-L/R log_(e) (i_(1)//4)/(i_1) implies L/R=T/(2 log_(e)2).
Topper's Solved these Questions
Similar Questions
An electric bulb rated for 500 watts at 100 volts is used in a circuit having a 200 volts supply. The resistance R that must be put in series with the bulb, so that the bulb delivers 500 watt is …………ohm.
View SolutionConsider an evacuated cylindrical chamber of height h having rigid conducting plates at the ends and an insulating curved surface as shown in the figure. A number of spherical balls made of a light weight and soft material and coated with a conducting material are placed on the bottom plate. The balls have a radius r<<h. Now a high voltage source (HV) is connected across the conducting plates such that the bottom plate is at +V0 and the top plate at −V0. Due to their conducting surface, the balls will get charged, will become equipotential with the plate and are repelled by it. The balls will eventually collide with the top plate, where the coefficient of restitution can be taken to be zero due to the soft nature of the material of the balls. The electric field in the chamber can be considered to be that of a parallel plate capacitor. Assume that there are no collisions between the balls and the interaction between them is negligible. (Ignore gravity)
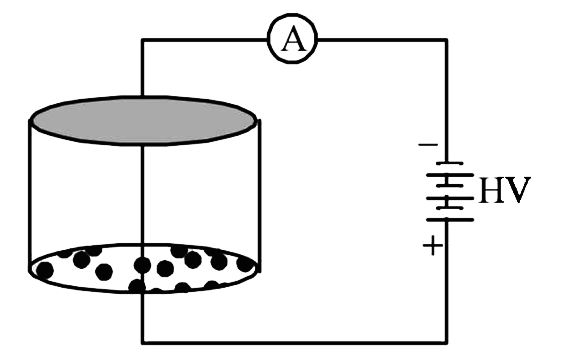
Which one of the following statements is correct?
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
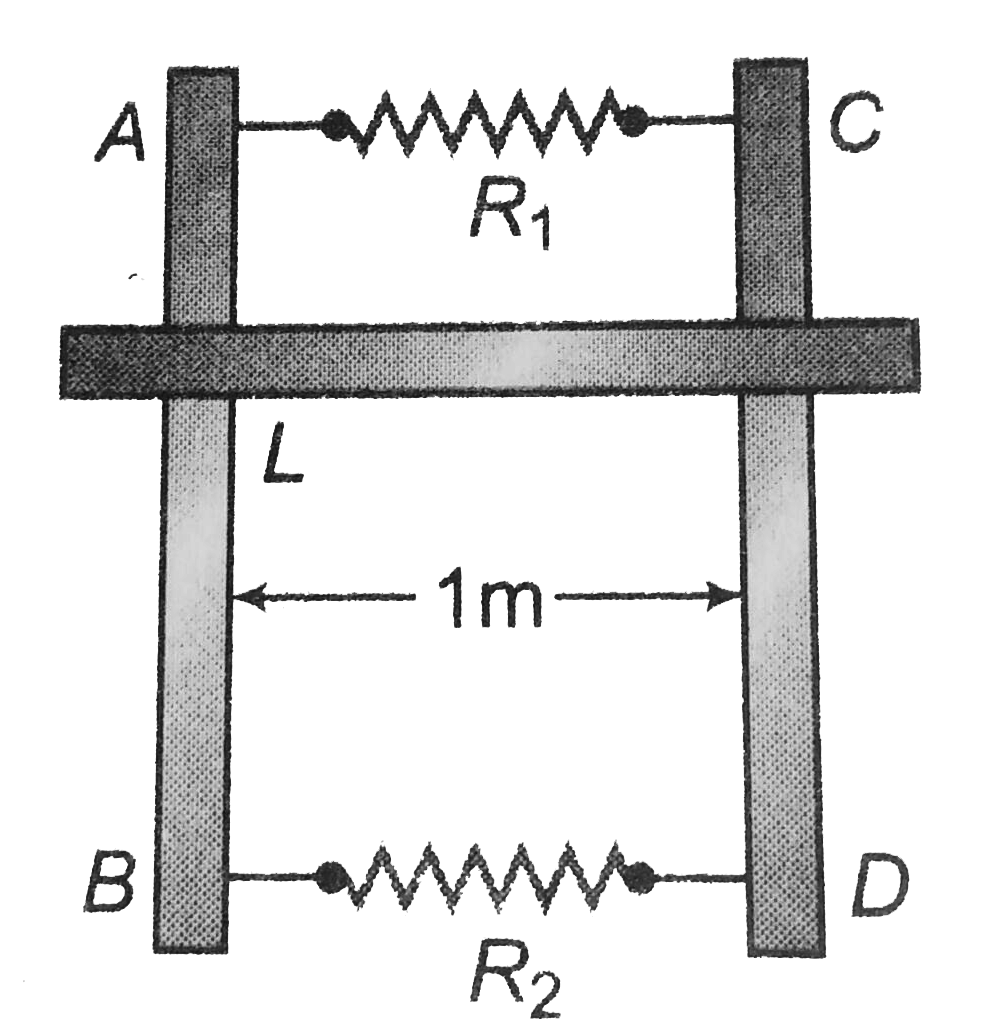
The terminal velocity fo the bar L will be
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
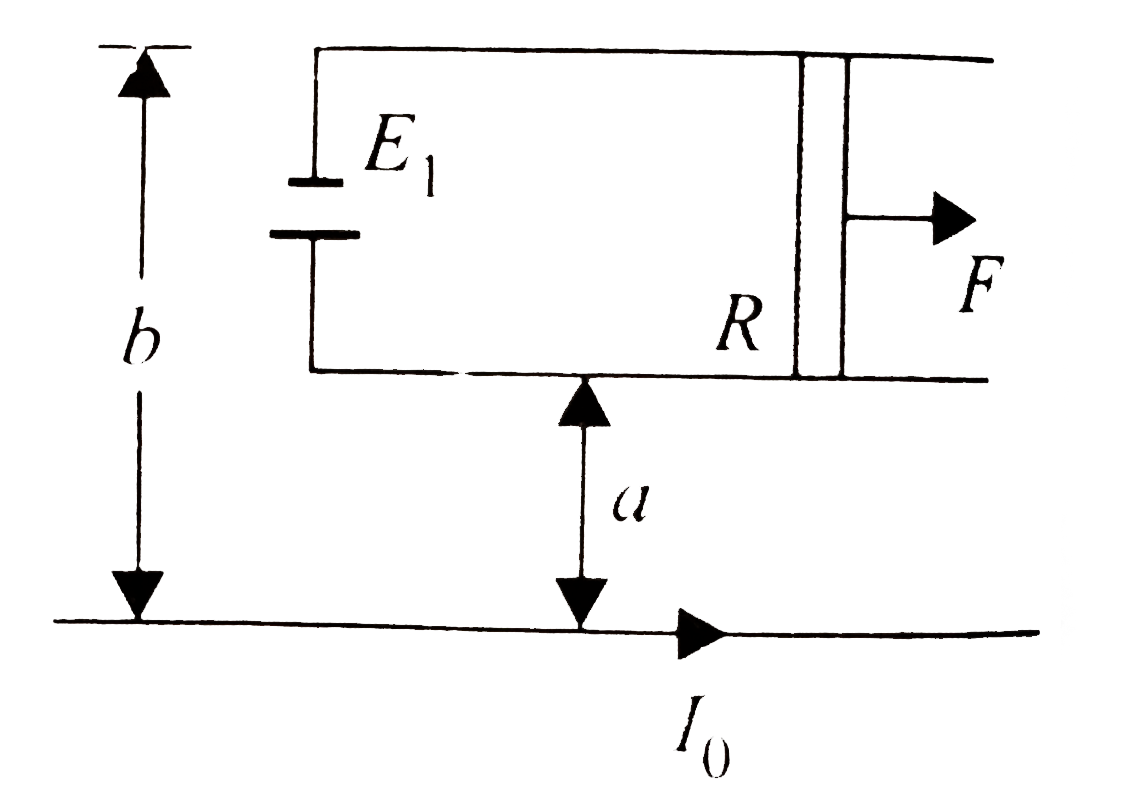
Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
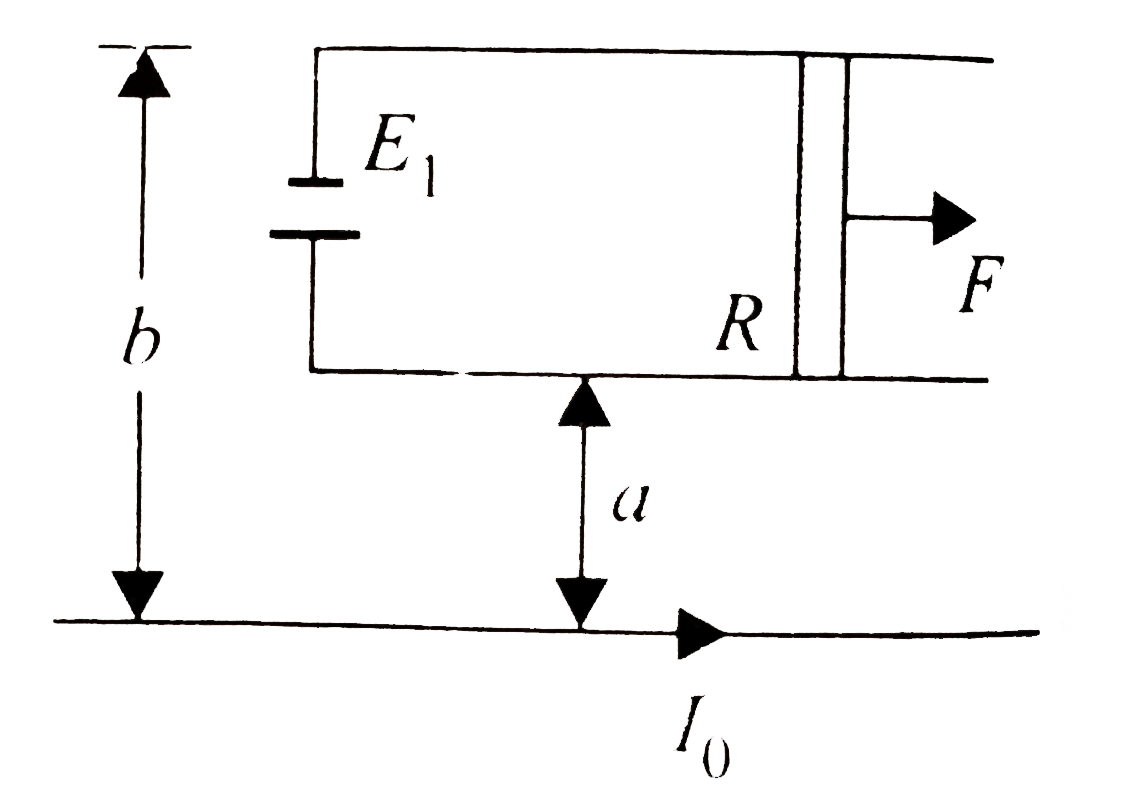
Find the value of F if the rod slides with constant velocity
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
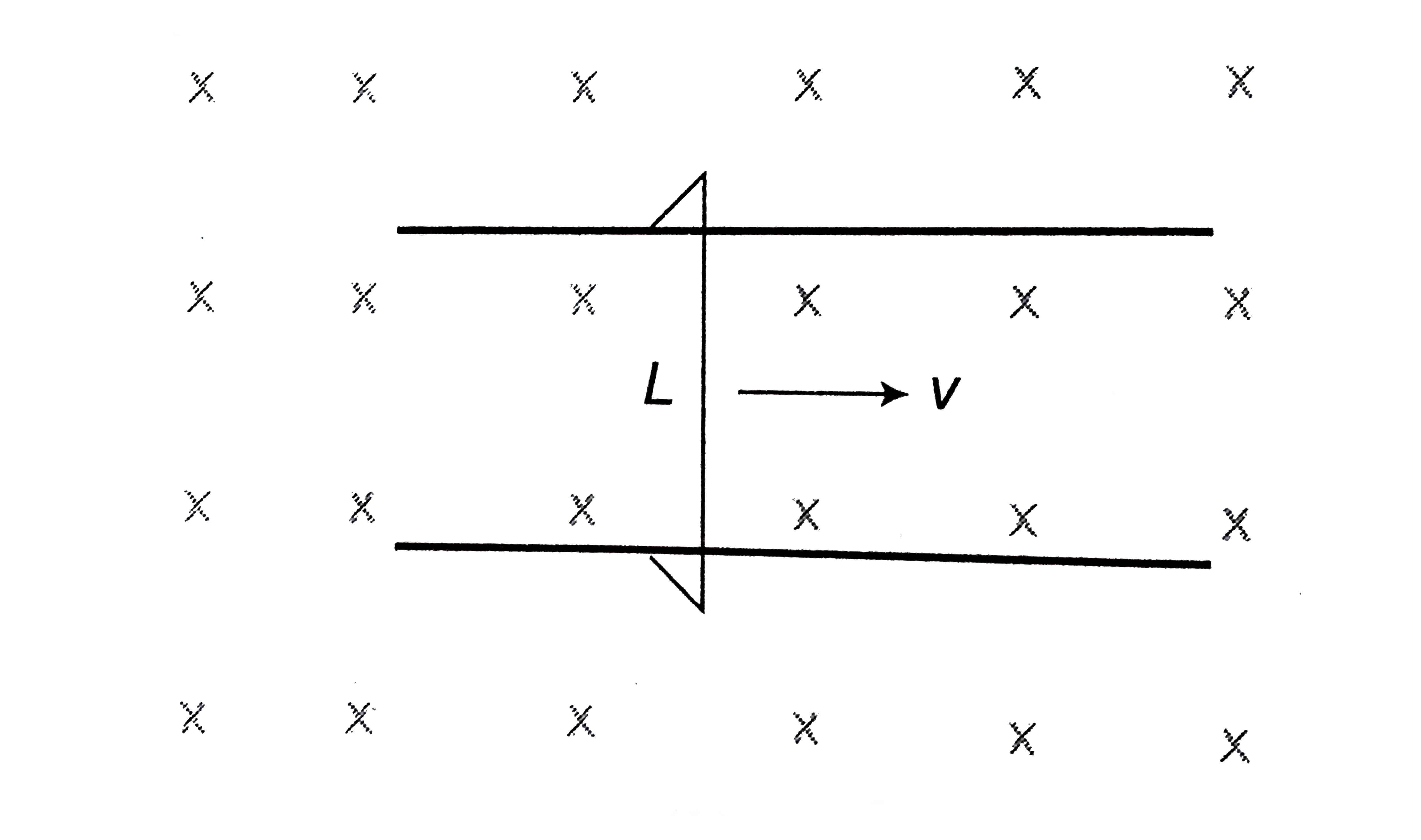
View SolutionTwo long fixed parallel vertical conducting rails AB and CD are separated by a distance L. They are connected by resistance R and a capacitance C at two ends as shown in the figure. There is a uniform magnetic field B directed horizon- tally into the plane of the figure. A horizontal metallic bar of length L and mass m can slide without friction along the rails. The bar is released from rest at t = 0. Neglect resistance of bar and rails and also neglect the self inductance of the loop.
(a) Find the maximum speed acquired by the bar after it is released.
(b) Find the speed of the bar as a function of time t.
View SolutionFigure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
View SolutionA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?

View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)

The terminal velocity fo the bar L will be
View SolutionA metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.

View Solution
