Velocity of particle moving along positive x-direction is . Here,t is in seconds. At time tha x coordinate of particle is zero. Find the time when the particle is at a distance of 60 m from origin.
The correct Answer is:B
Comparing with we have,
and
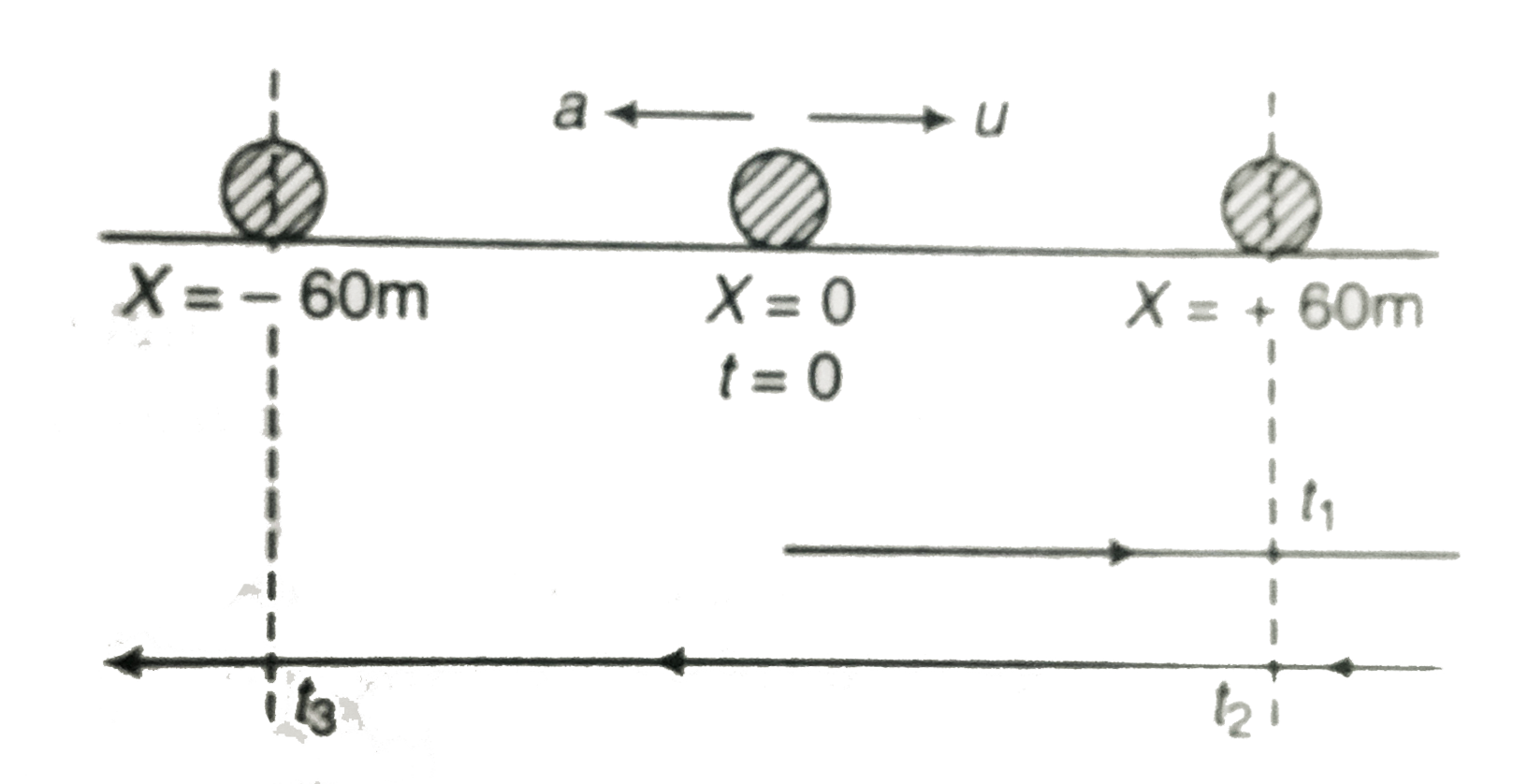
Distance of 60m from origin may be at
and .
From the figure, we can see that at these two points
particle is at three times and
For or and
Solving this equation, we get
and
For or
Solving this equation, we get positive value of t as
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective45videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle moving along the x axis has a position given by x=54t−2.0t3m. At the time t=3.0s, the speed of the particle is zero. Which statement is correct ?
A4.3×104m/s2, southB9.4×104m/s2, northC5.1×104m/s2, northD2.2×103m/s2, south - Question 2 - Select One
Velocity v of a particle moving along x axis as a function of time is given by v=2tm/s. Initially the particle is to the right of the origin and 2m away from it. Find the position (distance from origin) of the particle after first 3s.
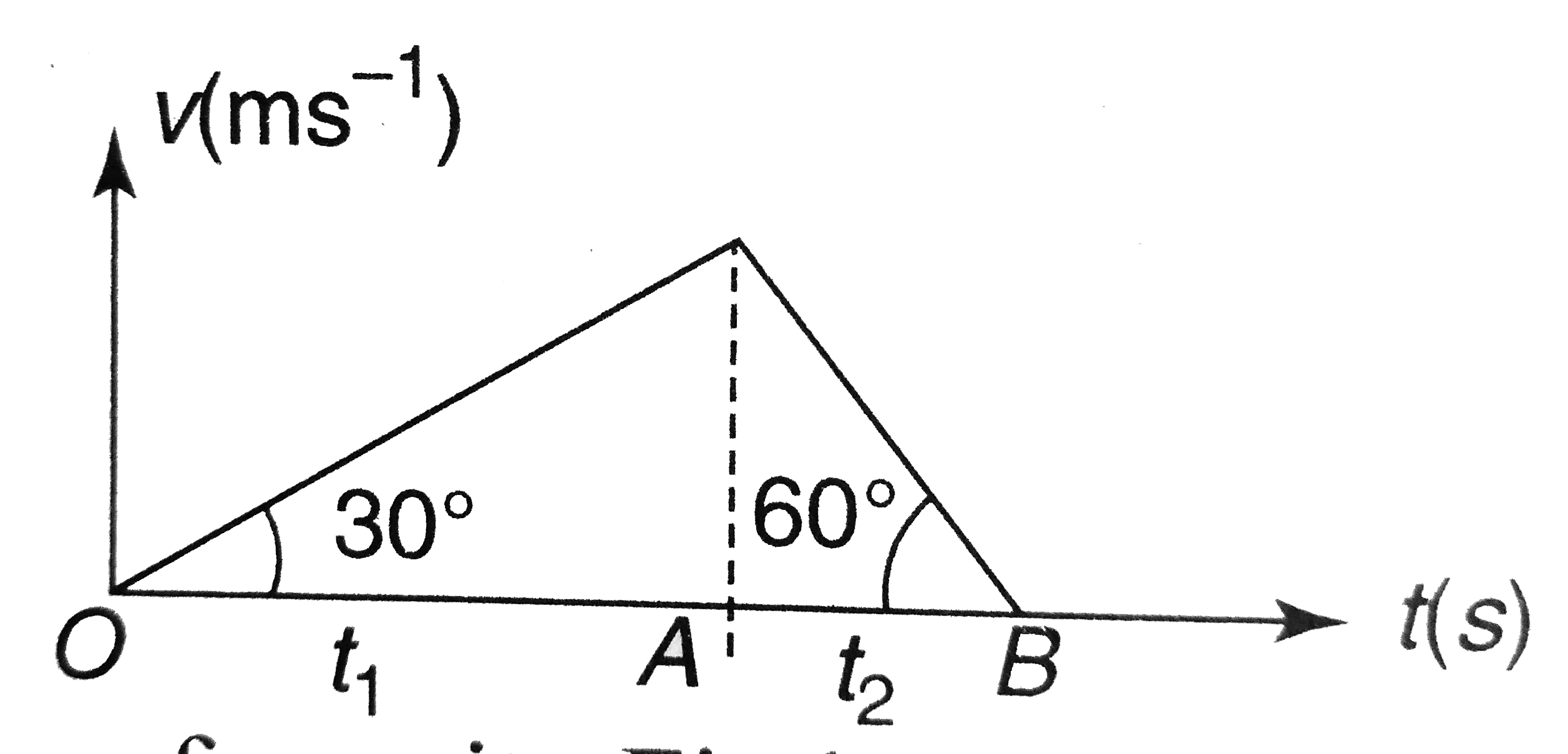 A5 mB7 mC11 mD9 m
A5 mB7 mC11 mD9 m - Question 3 - Select One
vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
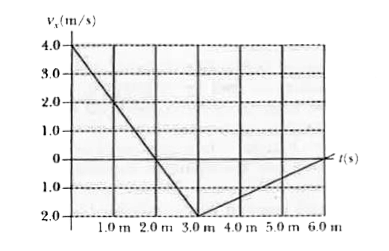 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A particle is moving along x-axis. At time t=0, Its x-coordinate is x=−4m. Its velocity-time equation is v=8−2t where, v is in m//s and t in seconds.
(a) At how many times, particle is at a distance of 8m from the origin?
(b) Find those times.View SolutionAt the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis. Its velocity varies with time as v=v0(1−t/τ), where v0 is the initial velocity vector whose modulus equals v0=10.0cm/s, τ=5.0s. Find:
(a) the x coordinate of the particle at the moments of time 6.0, 10, and 20s,
(b) the moments of time when the particles is at the distance 10.0cm from the origion,
(c) the distance s covered by the particle during the first 4.0 and 8.0s, draw the approximate plot s(t).View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.View Solution[" Velocity of a particle moving along "x" -axis "],[" as a function of time is given as "v=(4-],[t^(2))m/s," where "t" is time in second.The "],[" displacement of particle during "t=0s" to "t],[=1s" is "]
View SolutionA particle is moving along positive X direction and is retarding uniformly. The particle crosses the origin at time t=0 and crosses the point x=4.0m at t=2s.
(a) Find the maximum speed that the particle can possess at x=0.
(b) Find the maximum value of retardation that the particle can have.View Solution

