Question

A particle moves in a straight line with constant acceleration a. The displacements of particle from origin in times $t_1,t_2\text{and}{t}_{3}are{s}_1,s_2\text{and}{s}_3$ respectively. If times are in AP with common difference d and displacements are in GP, then prove that $a=\frac{{(\sqrt{s_1}-\sqrt{s_3})}^2}{d^2}$

Answer

A

Explanation

Let us draw v-t graph of the given situation, area of
which will give the displacement and slope the
acceleration.

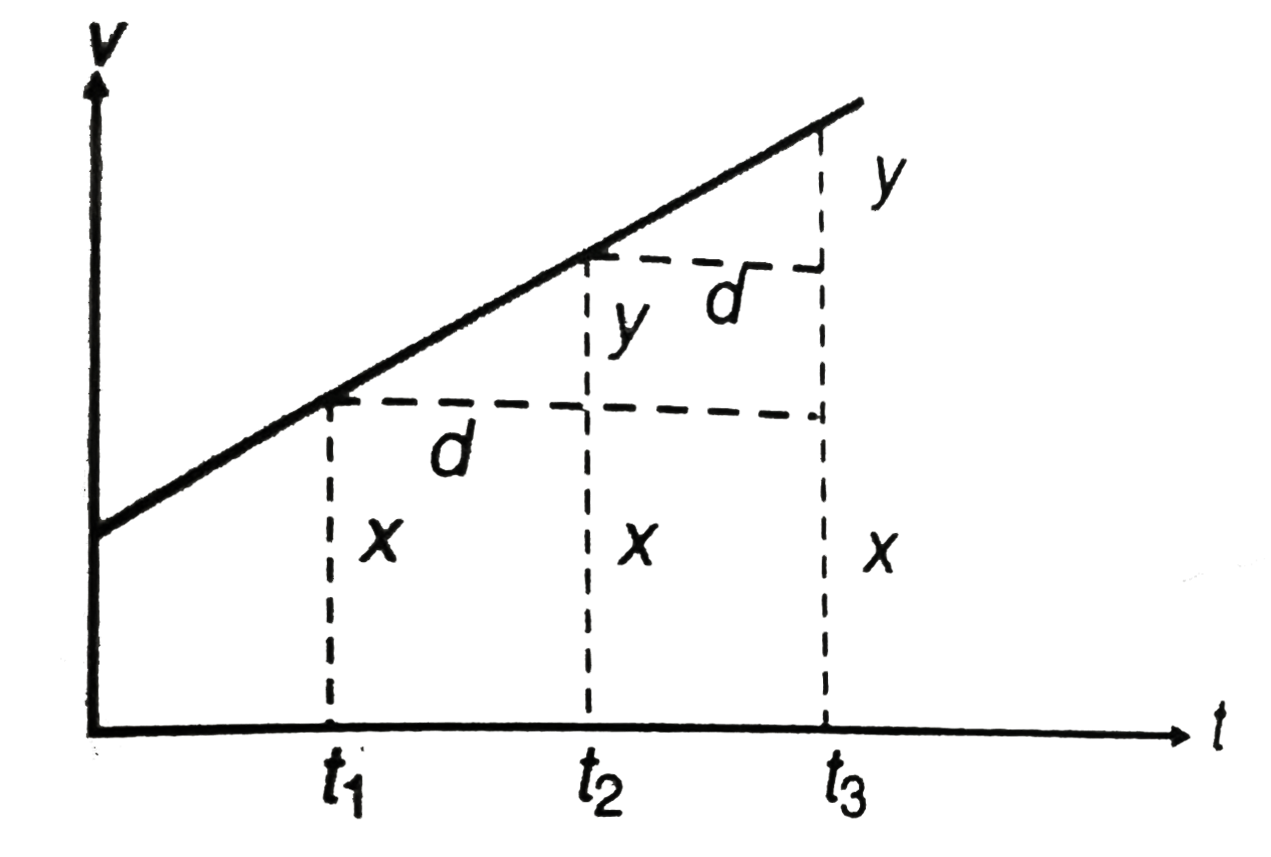
`s_2-s_1=xd+1/2yd…(i)`
`s_3-s_2=xd+yd+1/2yd ….(ii)`
Subtracting Eq. (i) from Eq. (ii), we have
`s_3+s_1-2s_2=yd`
or `s_3+s_1-2sqrt(s_1s_3)=yd (s_2=sqrt(s_1s_2))`
Dividing by `d^2` both sides we have,
`(sqrt s_1-sqrt s_3)^2/(d^2)=y/d`
=slope of v-t graph =a. Hence proved