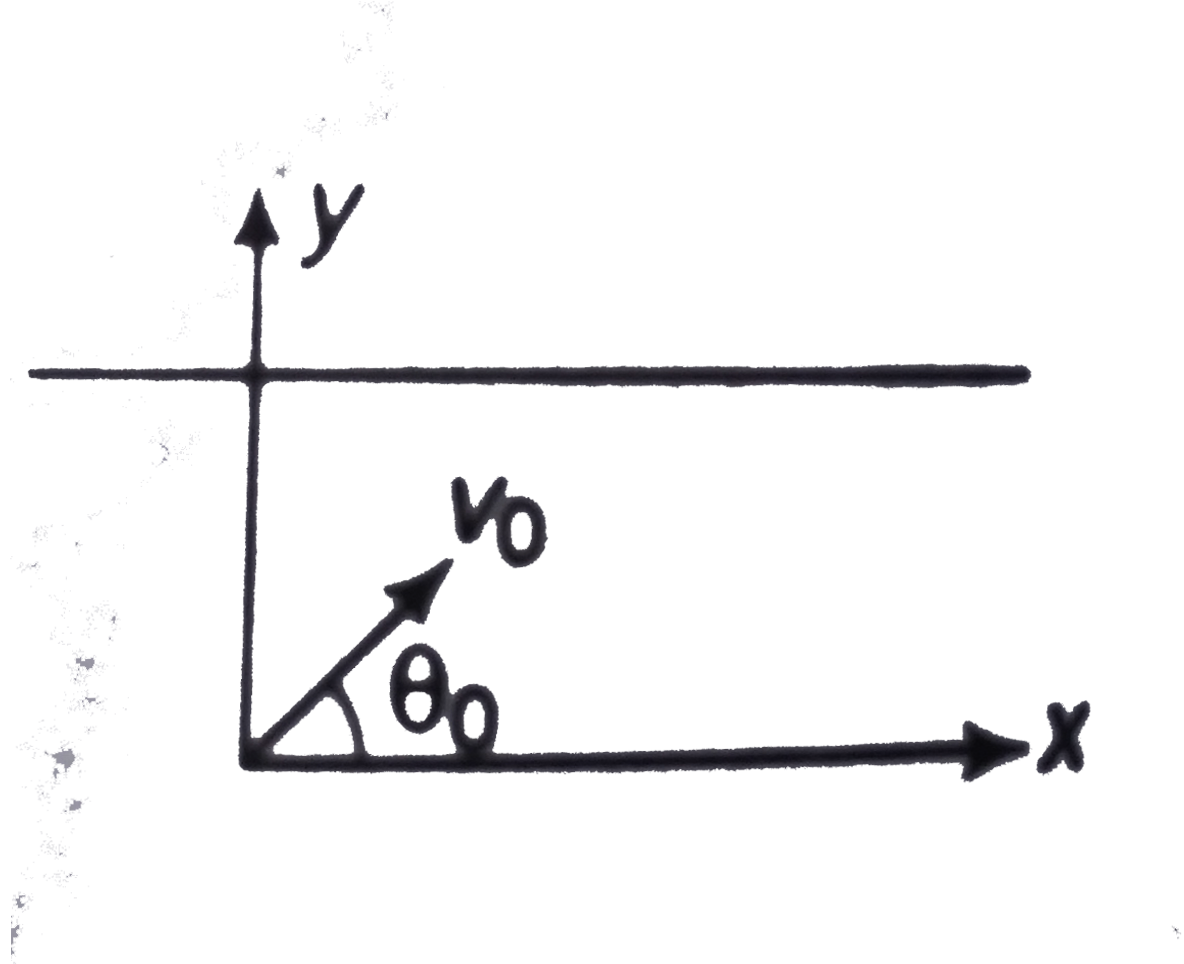
A projectile of mass m is fired into a liquid at an angle θ0 with an initial velocity v0 as shown. If the liquid develops a frictional or drag resistance on the projectile which is proportional to its velocity, i. e. F=−kv where k is a positive constant, determine the x and y components of its velocity at any instant. Also find the maximum distance xmax that it travels?
The correct Answer is:A, C
ax=dvxdt=−kvcosθm=−kmvx
∴dvxvx=−kmdtor∫vxv0cosθ0dvxvx=−km∫t0dt
or vx=v0cosθ0e−kmt …(i)

Similarly,
ay=dvydt=−kvsinθm−g=−(kmvy+g)
or ∫vyv0sinθ0dvykmvy+g=−∫t0dt
or mk[ln(kmvy+g)]vyv0sinθ0=−t
or (kmvy+g)(kmv0sinθ0+g)=e−kmt
or vy=mk[(kmv0sinθ0+g)e−kmt−g] ...(ii)
(b) Eq. (i) can be written as
dxdt=v0cosθ0e−kmt
or ∫x0dx=v0cosθ0∫t0e−kmtdt
or x=(m v_0 cos theta_0)/k [1-e^(-k/m t)]<br>orx_m=(m v_0 cos theta_0)/k<br>att=oo
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE41videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE23videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
A box is thrown with velocity v0 on top of a rough table of length l. Assume friction on the object is such that during its motion, its acceleration is given as a=−kv, where k is a positive constant. Find the velocity of the box when it leaves the edge of the table. Also find the time after which it falls off the edge.
View SolutionA small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the momentum of the particle
at t<υ0sinθg.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A projectile of mass m is launched with an initial velocity →vi making an angle θ with the horizontal as shown in figure. The projectile momentum of the particle about the origin when it is at the highest point of its trajectory is.
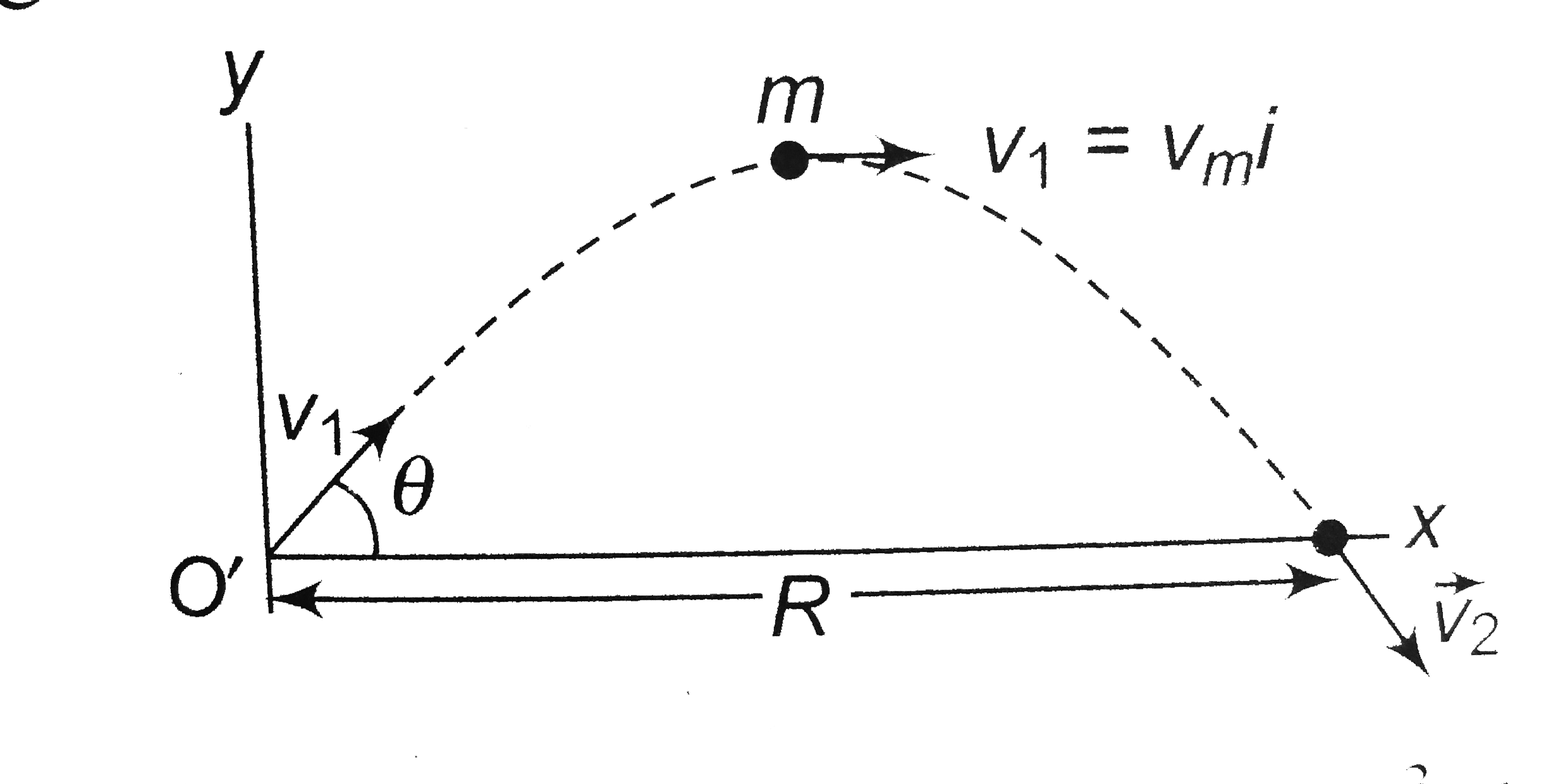 .A−m3isinθ2cosθ2gˆkBm3isinθ2cosθ2gˆkC−m3isinθ2cosθgˆkD2m3isinθ2cosθgˆk
.A−m3isinθ2cosθ2gˆkBm3isinθ2cosθ2gˆkC−m3isinθ2cosθgˆkD2m3isinθ2cosθgˆk - Question 2 - Select One
A projectile is fired from the origin with a velocity v0 at an angle θ with x-axis. The speed of the projectile at an altitude h is .
Av0cosθB√v20−2ghC√v20sin2θ−2ghDNone of these - Question 3 - Select One
A projectile is fired at an angle of 30∘ with the horizontal such that the vertical component of its initial velocity is 80m/s. Find approximatly the velocity of the projectile at time T/4 where T is time of flight.
A180m/sB155m/sC145m/sD140m/s
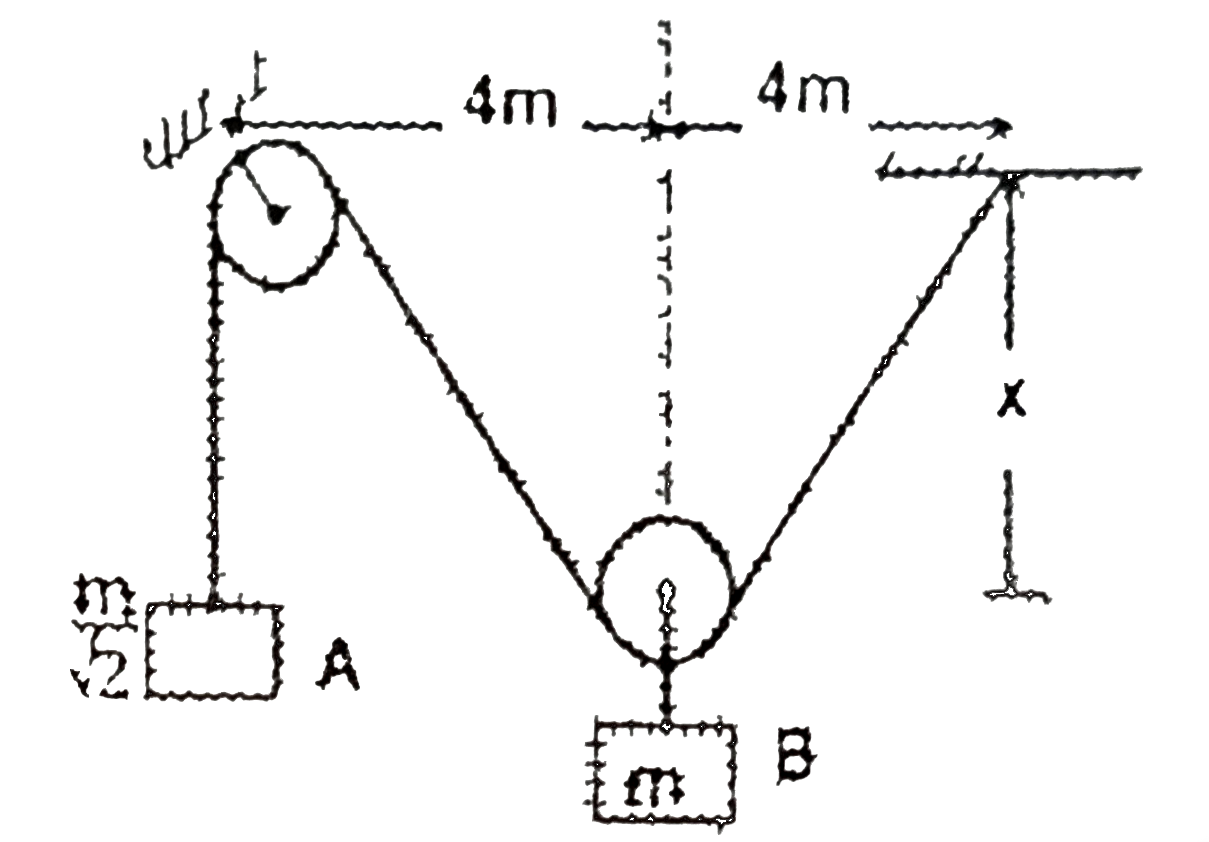
The system of mass A and B shown in the figure is released from rest with x=0, determine the velocity of mass B when x=3m. Also find the maximum displacement of mass B.
 View Solution
View SolutionA particle of mass m and charge q is projected into a region having a uniform magnetic field B0. Initial velocity (v0) of the particle is perpendicular to the magnetic field. Apart from the magnetic force the particle faces a frictional force which has a magnitude of f = kv where v is instanta- neous speed and k is a positive constant.
(a) Find the radius of curvature of the path of the particle after it has travelled through a distance of x0=mv02K.
(b) Plot the variation of radius of curvature of the path of the particle with time (t).View SolutionA sky diver of mass m is making a delaged drop with an initial velocity v0=0. Find the law by which the sky diver's speed varies before the parachute is opened if the drag is proportional to the sky diver's speed. Also solve the problem when the sky diver's initial velocity has horizontal component v0 and vertical componment zero.
View SolutionA body of mass m is thrown straight up with velocity v0(v0<<ve) Find the velocity v with which the body comes down if the air drag equals kv2, where k is a positive constant and v is the velocity of the body.
View SolutionA projectile of mass 20 kg is fired with a velocity of 400m/sat an angle of 45∘ with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
View Solution

