A smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

mgcosθ
less than mgcosθ
greater than mgcosθ
may be less or greater than mgcosθ depending upon whether M is less or greater than m
The correct Answer is:B
During motion of block , a component of its acceleration comes in the direction of mgcosθ Therefore 
mgcosθ>N
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m is initially lying on a wedge of mass M with an angle of inclination θ as shown in figure. Calculate the displacement of the wedge when the block is released and reaches to the bottom of the wedge.

View Solution
Knowledge Check
A block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
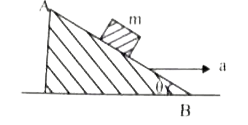 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
A block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA block of mass m is kept on an inclined plane of mass 2m and inclination α to horizontal. If the whole system is accelerated such that the block does not slip on the wedge then :
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
View SolutionA block of mass m is placed on a smooth wedge of incination θ. The whole system s acelerated horizontally so tht the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
View SolutionA block of mass 1kg is at rest relative to a smooth wedge moving leftwards with constant acceleration a=5m/s−2 .Let N be the normal reation between the block and the wedge . Then (g=10m/s−2)

View Solution