In the arrangement shown in the figure the mass M is very heavy compared to m(M>>m). The tension T in the string suspende from the ceiling is

4mg
2mg
zero
None of these
The correct Answer is:B
a=Net pulling forceTotal mass=(M−m)g(M+m) …(i)
Since M>>m
∴M−m≈M+m=M
Subtituting in Eq. (i),we have
a=g
FBD of m T−mg=ma=mg
∴T=2mg
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A mass of 3kg is suspended by a rope of length 2m from the ceilling A force of 40N in the horizontal direction is applied atmidpoint P of the rope the as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, g=10m/s2) .
View SolutionIn the arrangement as shown, tension T2 is (g=10m/s2)
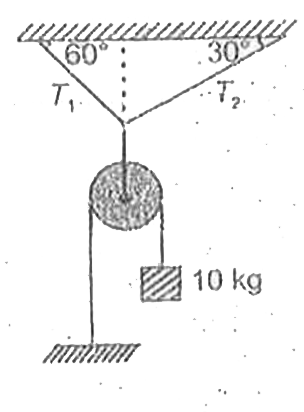
View Solution
Knowledge Check
The tension in the string shown in figure m−2m→F is.
AF/3BF/6CF/2D2FThe block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgIn the arrangement shown in figure, there is a friction force between the blocks of masses m and 2m. The mass of the suspended block is m. The block of mass m is stationary with respect to block of mass 2m. The minimum value of coefficient of friction between m and 2m is
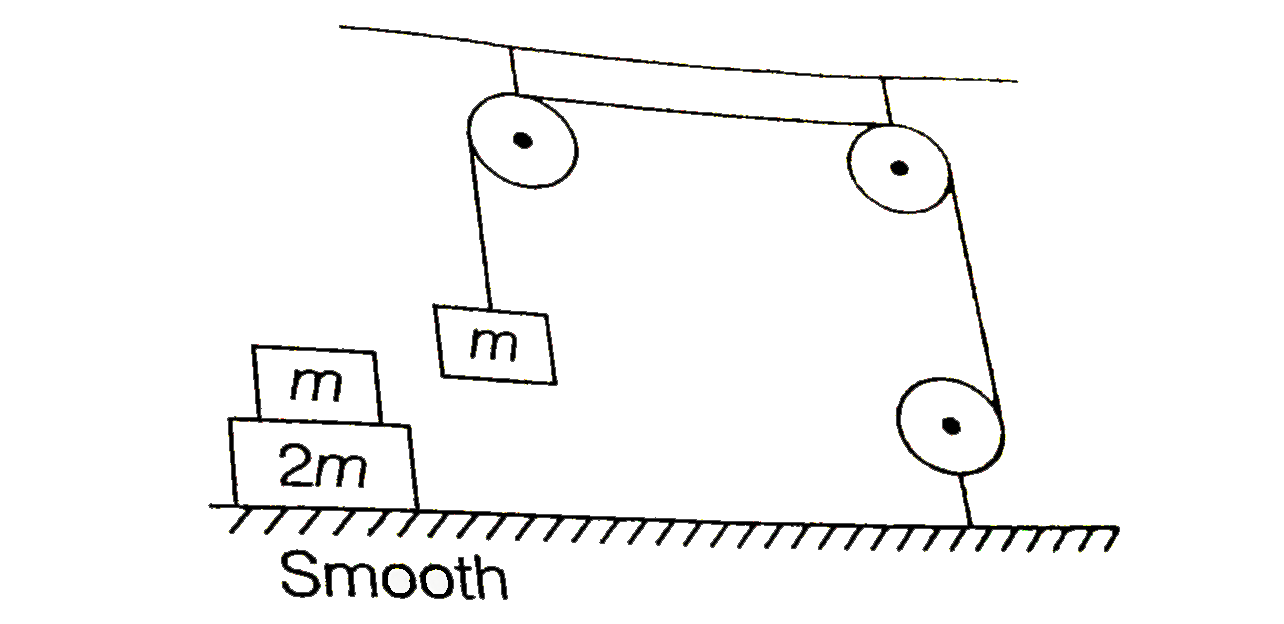 A12B1√2C14D13
A12B1√2C14D13
A mass of 3kg is suspended by a rope of length 2m from the ceiling. A force of 40 N in the horizonal direction is applied at midpoint P of the rope as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling? (Neglect the mass of the rope, g=10m/s2)
View SolutionIn the arrangement as shown, tension T2 is -
(g=10m/s2)
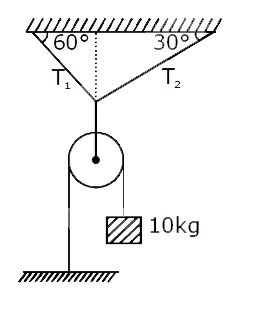
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
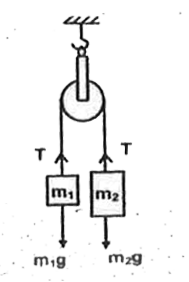
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
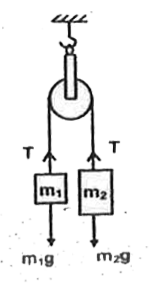
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View SolutionA mass M of 100 kg is suspended with the use of strings A, B 90 and C as shown in the figure, where W is the vertical wall and R is a rigid horizontal rod. The tension in the string B is
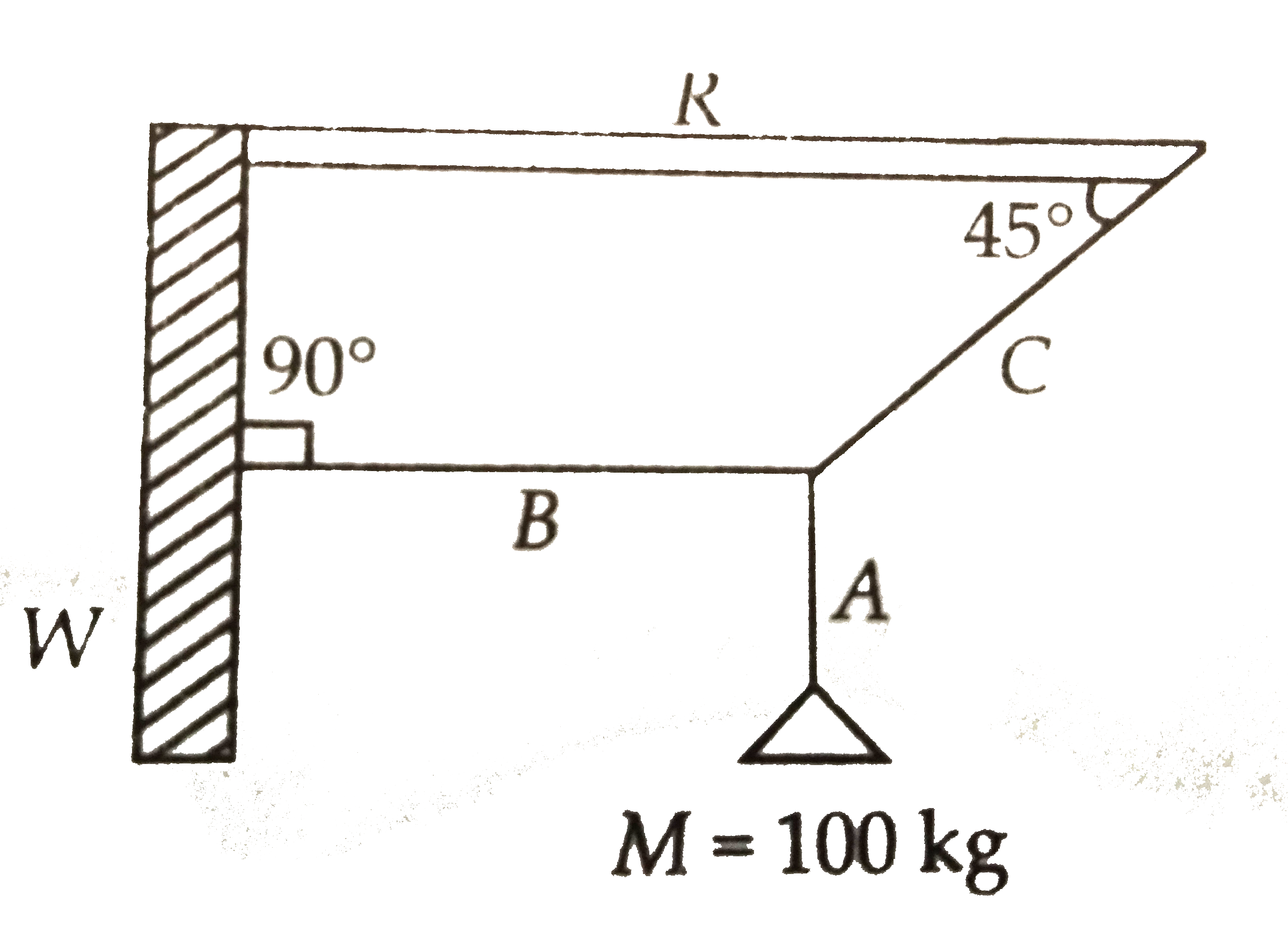
View Solution