
A solid ball rolls down a parabolic path ABC from a height h as shown in figure. Portion AB of the path is rough while BC is smooth. How high will the ball climb in BC?
3h5
4h9
5h7
None of these
The correct Answer is:C
At B, total kinetic energy =mgh
Here, m= mass of ball
The ratio of ratational to translational kinetic energy would be.
KRKT=25⇒∴KR=27mgh and KT=57mgh
In portiona BC, friction is absent. therefore, rotational kinetic energy will remain constant and translational kinetic energy will convert into potential energy. Hence, if H be the height to which ball climbs in BC, then
mgH=KT or mgH=57mgh or H=57h
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example1videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A ball is released from height h as shown in fig. Find the condition for the particle to complete the circular path.
View SolutionA spherical rigid ball is realeased from rest and starts rolling down an inclined plane from height h=7m, as shown in the figure. It hits a block at rest on the horizontal plane (assme elastic collision). If the mass of both the ball and the block is m and the ball is rolling without sliding, then the speed of the block after collision is close to
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small ball is rolled with speed u from point A along a smooth circular track as shown in figure. If x=3R, then

What is the minimum value of x for which the ball can reach the point of projection after reaching C?A2RB5RC3RD52R - Question 2 - Select One
A solid sphere rolls down a parabolic path , whose vertical dimension is given by y=kx2 and base of the parabola is at x = 0 . During the fall the sphere does not slip, but beyond the base the climb is frictionless. If the sphere falls through a height h, the height above the base that it would climb is
A54B7hC75hD57h - Question 3 - Select One
A uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
A5h/8B3h/5C5h/7D7h/9
A smooth ball is released from rest from a height h as shown in figure. It slides down the first inclined plane and collides with the second inclined plane.
a. If e=0, find the speed of the ball just after leaving the inclined plane 1.
b. If the particle mioves horizontally just after the collision find e.
 View Solution
View SolutionA particle travels along the path ABC, as shown in the figure given below, AB = BC = l, calculate the path length and displacement of the particle
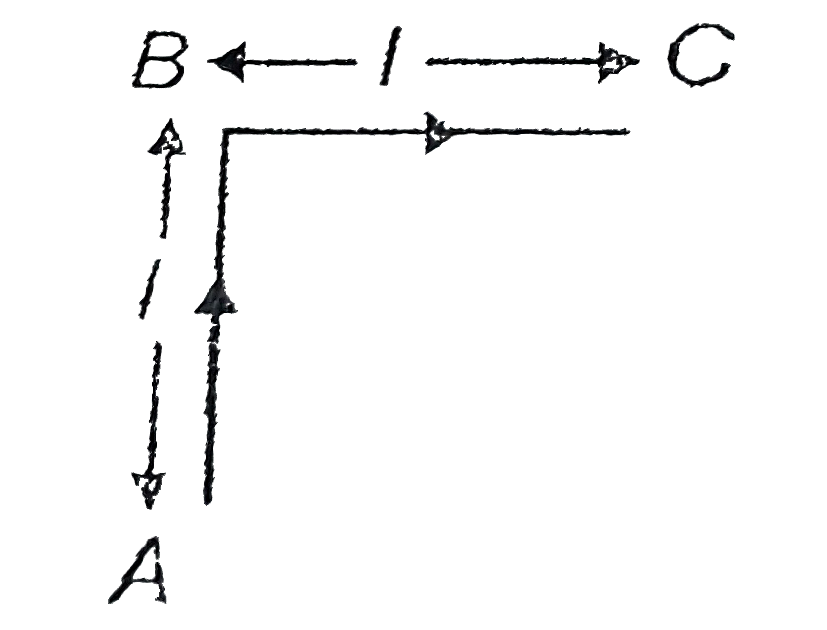 View Solution
View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
View SolutionA solid sphere rolls down a smooth inclined plane of height h. If it stats from rest then the speed of the sphere when it reaches the bottom is given by
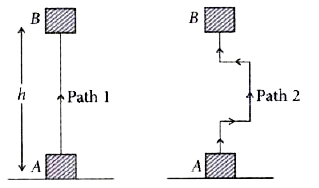
View SolutionA block is raised from position A to B by taking two different paths as shown in the figure. If AB = h, then
 View Solution
View Solution

