
A solid shere of mass m and radius R is kept over a rough ground. A time varying force F=2t is acting at the topmost point as shown in figure.
(a). Find angular momentum of the sphere about the bottommost point as a function of time t
(b). Does this result depend on the fact whether the ground is rough or smooth?

(a). Suppose f is the force of friction acting on the sphere in forward directionn as shown in figure.
taking torque about bottommost point O. Torque of friction is already zero. As this force already passes through O. torque of applied force is only there.
τ=F×r⊥
=(2t)(2R)=4RT
As, this toque is a function of time
∴ angular impulse =∫t0τdt=∫t0(4Rt)dt=2Rt2
this angular impulse is equal to change in angular momentum. Hence, angular momentum at time t is 2Rt2.
(b). This result is independent of the nature of surface (smooth or rough) as the torque of friction about bottommost point is already zero. it does not contribute in angular impulse and therefore in angular momentum.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
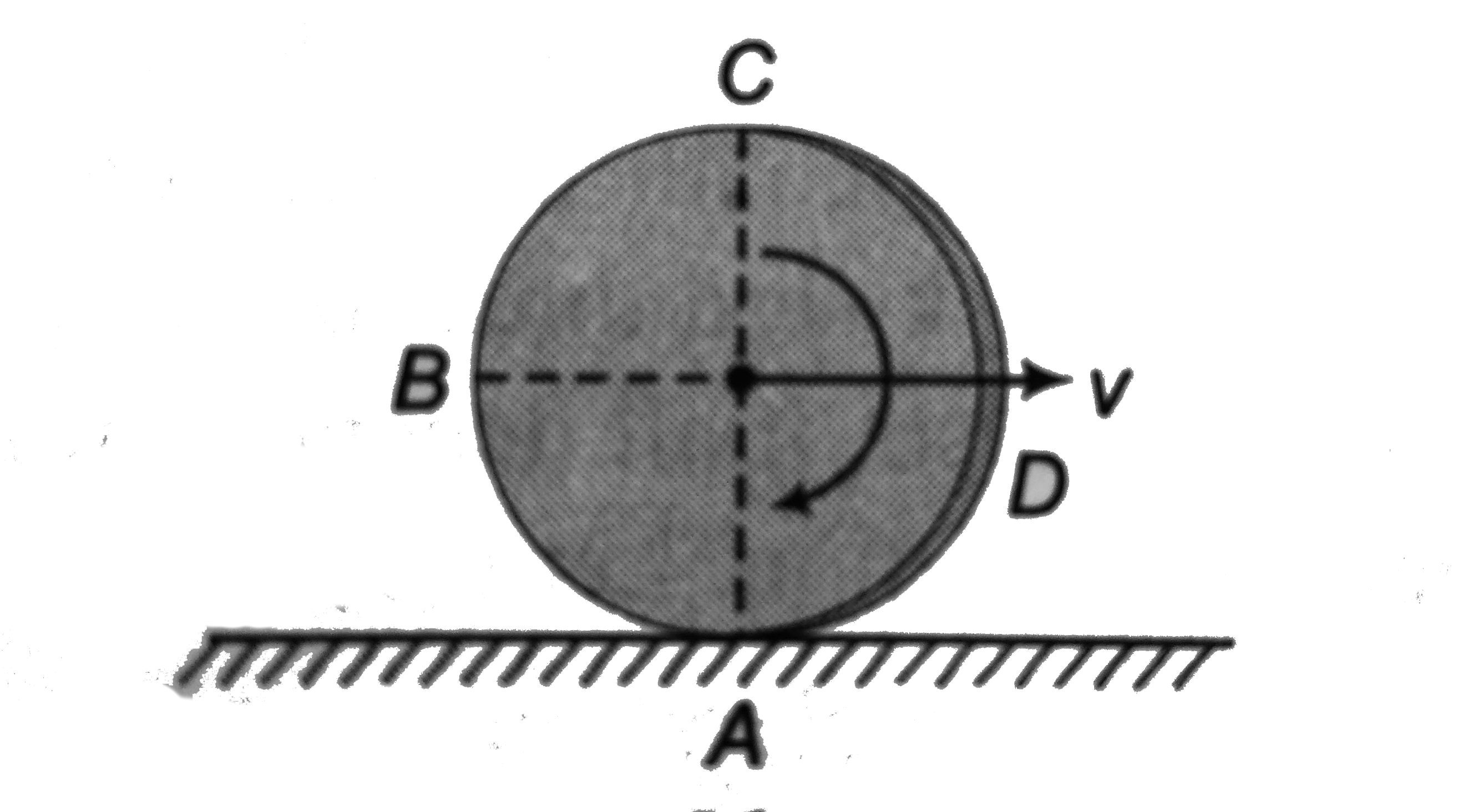
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA sphere of mass m and radius R is kept on a rough horizontal floor. Constant force Facts at the top point of sphere along tangent. If there is sufficient friction on the floor to support pure rolling then calculate acceleration of sphere.
View Solution
Knowledge Check
A time varying force F=2t is applied on a spool as shown in figure. The angular momentum of the spool at time t about bottommost point is:
 Ar2t2RB(R+r)2rt2C(R+r)t2Ddata is insufficient
Ar2t2RB(R+r)2rt2C(R+r)t2Ddata is insufficientA time varying force F=2t is applied on a spool as shown in figure. The angular momentum of the spool at time t about bottommost point is
 Ar2t2RB(R+r)2rt2C(R+r)t2DData insufficent
Ar2t2RB(R+r)2rt2C(R+r)t2DData insufficentA constant force F is applied at the top of a ring as shown in figure. Mass of the ring is M and radius is R. Angular momentum of particle about point of contact at time t
 Ais constantBincreases linearly with timeCis 2F R tDdecrease linearly with time
Ais constantBincreases linearly with timeCis 2F R tDdecrease linearly with time
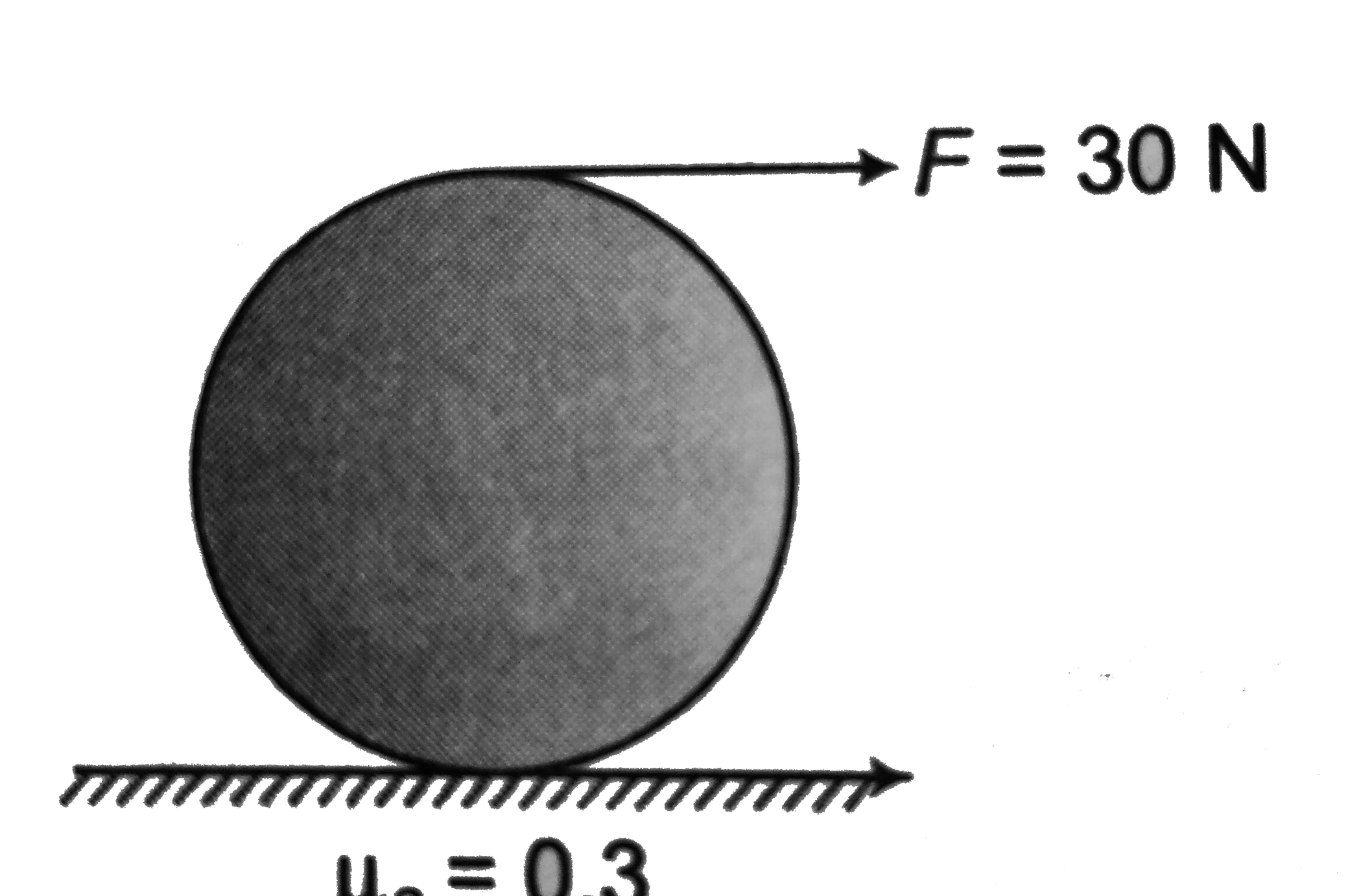
A solid sphere of mass 5 kg and radius 1m is kept over a rough surface as shown in figure. A force F=30N is acting at the topmost point.
(a). Check whether the pure rolling will take place or not
(b). Find direction and magnitude of friction actually acting on the sphere.
(c). Find linear acceleration a and angular acceleration α take g=10m/s2
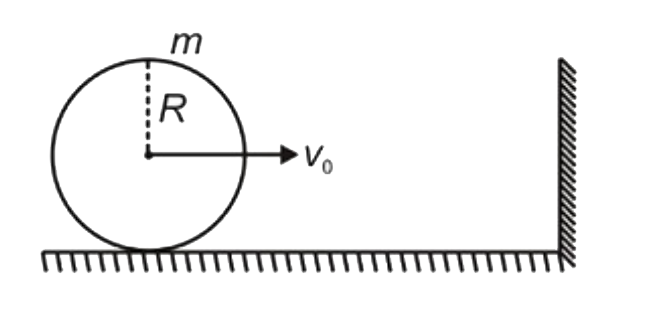
View SolutionA uniform solid sphere of mass m, radius R moving with velocity v0 is rolling without slipping on a frictionless surface vertical wall. Ratio of magnitude of angular momentum of the sphere and after the collision about its bottommost point is
View SolutionA ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View Solution
