
A thin massless thread is wound on a reel of mass 3 kg and moment of inertial 0.6 kg−m3 the hub radius is R=10cm and peripheral radius is 2R=20 cm the reel is placed on a rough table and the friction is enough to prevent slipping. find the acceleration of the centre of reel and of hanging mass of 1 kg.
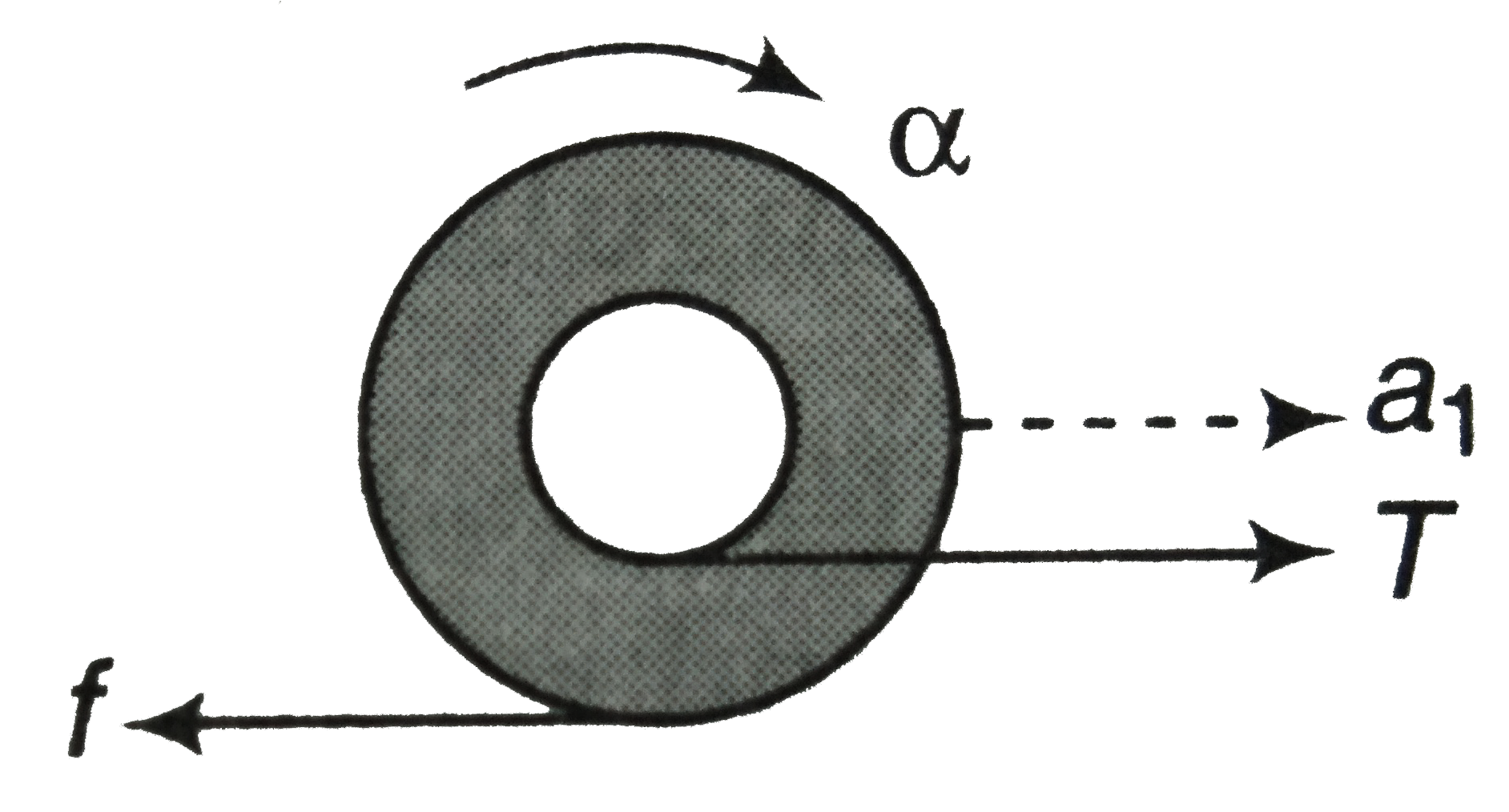
Here, number of unknowns are five:
a1= acceleration of centre of mass of reel
a2= acceleration of 1 kg block
α= angular acceleration of reel (clockwise)
T= tension in the string
f= force of friction
Acceleration equations:
Free bod diagram of reel is as shown in figure, (only horizontal forces are shown)
equations of motion are
T−f=3a1 ..(i)
α=τI=f(2R)−T.RI=0.2f−0.1T0.6=f3−T6 ..(ii)

Free body diamgram of mass is
equation of motion is Equation of motion is
10−T=a2 ..(iii)
contact equations
for no slipping condition a1=2Rα or a1=0.2α ..(iv)
and a2=a1−Rα or a2=a1−0.1α
solving the above five equations we get
a1=0.27m/s2 and a2=0.135m/s2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
Acceleration of centre of mass of sphere is
View SolutionA small pulley of radius 20 cm and moment of inertia 0.32kg−m2 is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition find the acceleration of the block ( in m/s2).
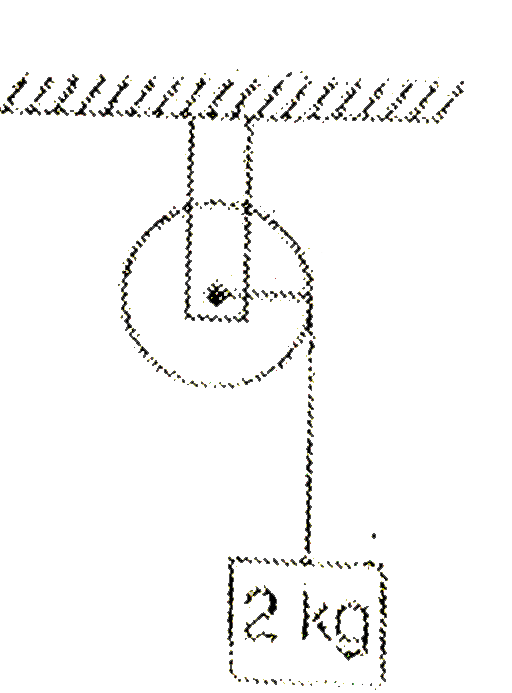
View Solution
Knowledge Check
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2m
A small pulley of radius 20 cm and moment of inertia 0.32kg−m2 is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition acceleration of the block will beA2m/s2B4m/s2C1m/s2D3m/s2A string is wound round the rim of a mounted flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel in rad/s2 is
A50B25C12.5D6.25
A cotton reel of mass m and moment of inertia I is kept at rest on as smooth horizontal surface. The reel has inner and other radius r and R respectively. A horizontal force F starts actings as shown in figure. Find the

a. acceleration of the centre of mass of reel.
b. angular acceleration of the reel
c. net acceleration of point of contact.
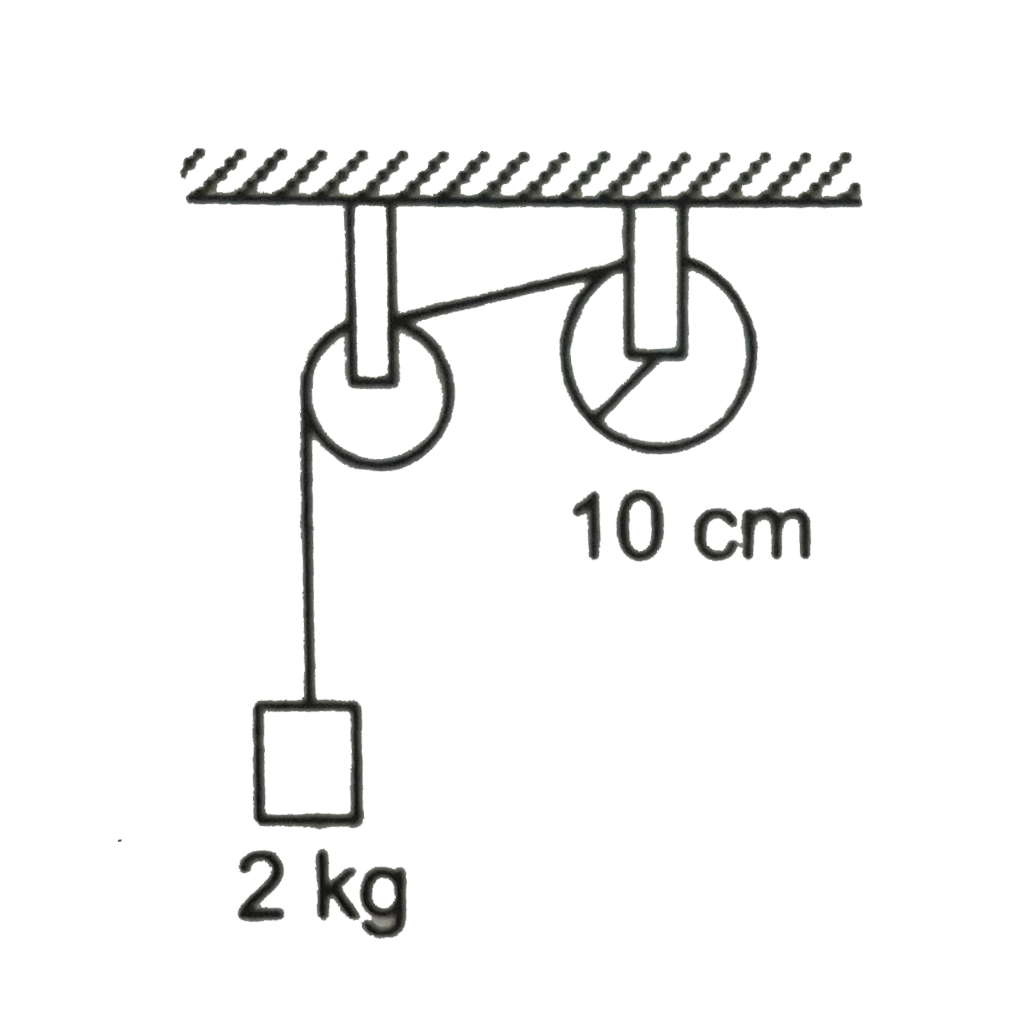
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mas 2.0 kg as shown in figure. Find the acceleration of the block.
View SolutionA cotton reel of mass m, radius R and moment of inertia I is kept on a smooth horizontal surface. If the string is pulled horizontally by a force F, find the (i) acceleration of CM, (ii) angular acceleration of the cotton reel.

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View Solution
in figure the cylinder of mass 10kg and radius 10 cm has a tape wrapped round it. The pully weighs 100 N and has a radius 5 cm. When the system is released the 5 kg mass comes down and the cylinder rolls without slipping. Calculate the acceleration and velocity of the mass as a function of time.
View Solution
