The tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in figure is T0 when the system is at rest. What will be the tension in the string if the system has an upward acceleration a?
 .
.
T0(1+ag)
T0(1−ag)
T0(1+ga)
T0(1−ga)
The correct Answer is:A
Let m be the mass of block.
Initially for the equilibrium of block,
F=T0+mg ...(i)
Here,F is the upthurst on the block.
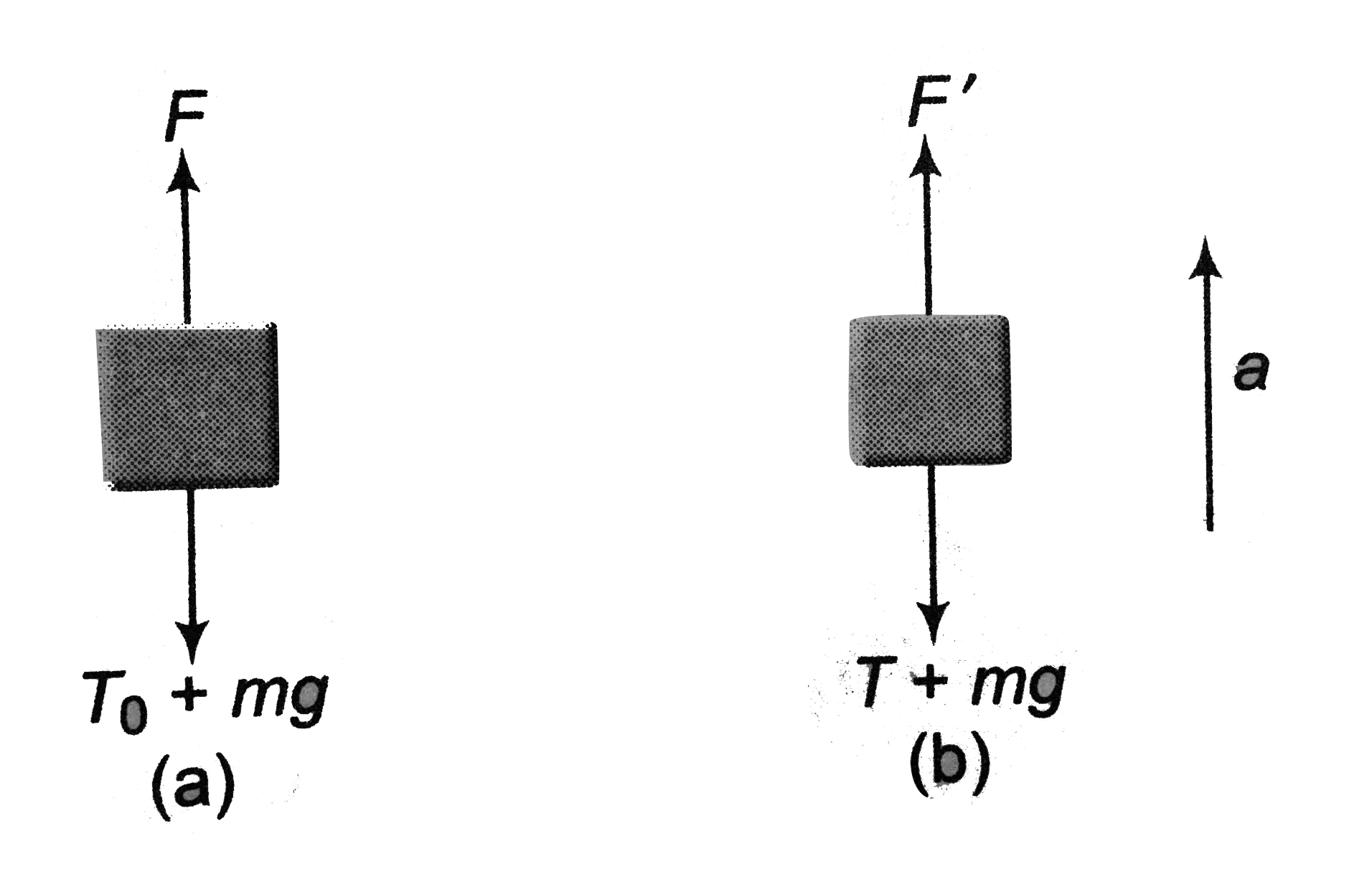
When the lift is accelerated upward, geff becomes g+a instead of g. hence,
F'=F(g+ag) ...(ii)
From Newton's second law,
F'−T−mg=ma ...(iii)
Solving Eqs. (i),(ii) and (iii), we get
T=T0(1+ag).
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples21videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
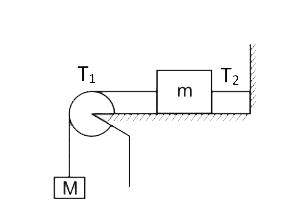
The tension in the string in the pulley system shown in
 .A5.7NB7NC7.5ND73.5N
.A5.7NB7NC7.5ND73.5N - Question 2 - Select One
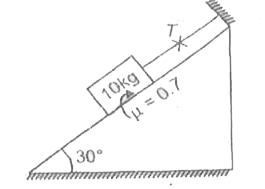
Find the tension T2 in the system shown in the figure.
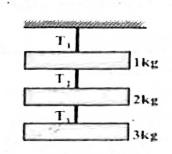 A1gNB2gNC5gND6gN
A1gNB2gNC5gND6gN
Consider the situation shown in figure. Find the acceleration of the system and the tension in the strings.
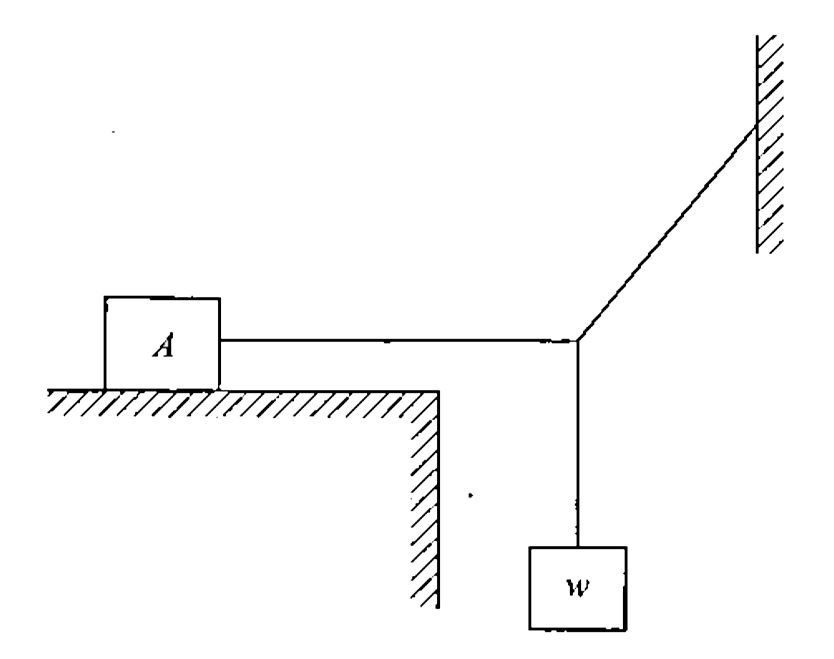 View Solution
View SolutionA string is holding a solid block below the surface of the liquid as shown in figure. If the system is given an upward acceleration a, then as compared to previous state.
 View Solution
View SolutionFor the system shown in the figure,the pulleys are light and frictionless.The tension in the string will be
View SolutionConsider the double Atwood's machine as shown in the figure
(a) Whatis acceleration of the masses?
(b) What is the tension in each string?
 View Solution
View SolutionConsider the double Atwood's machine as shown in the figure
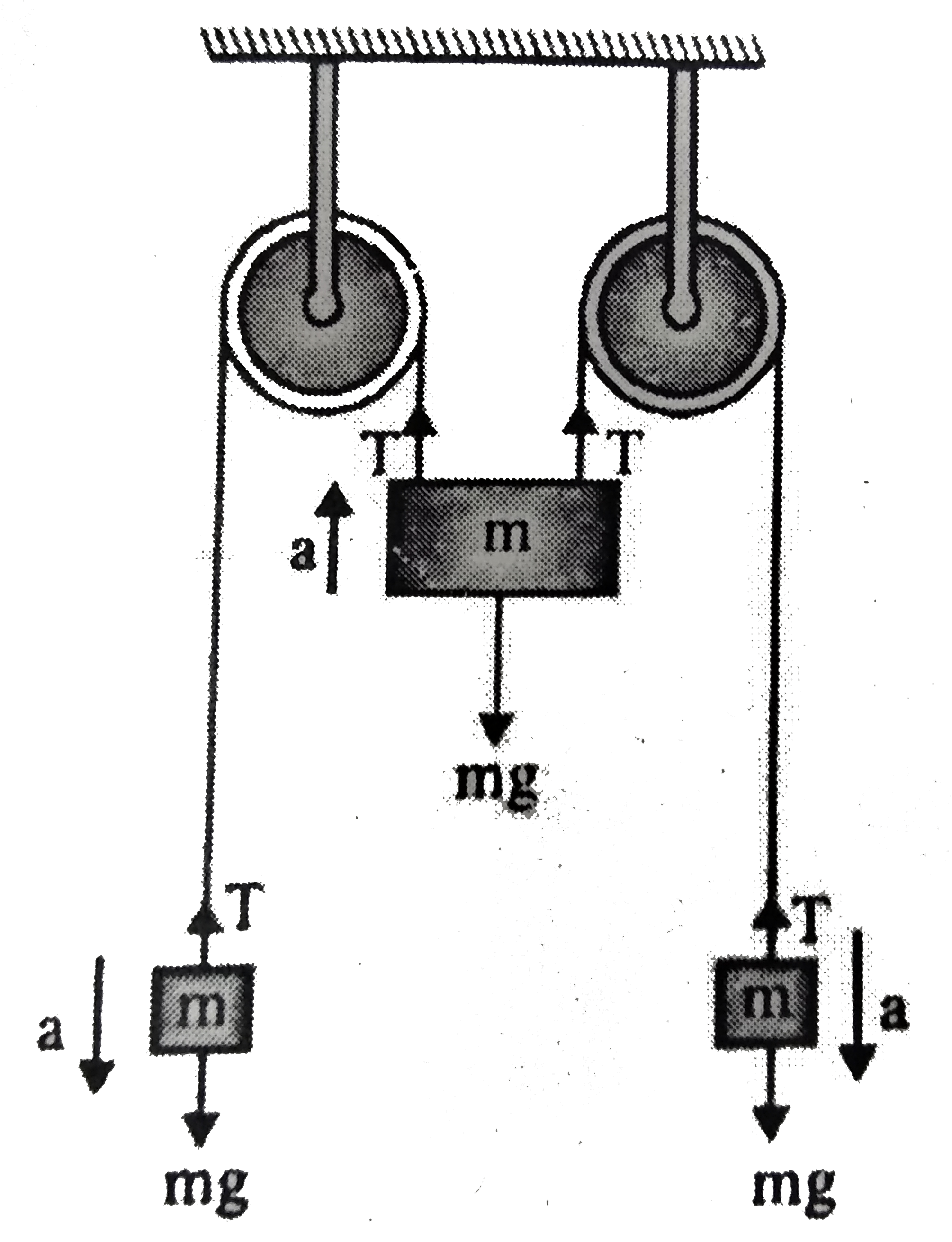
(a) What is acceleration of the masses?
(b) What is the tension in each string?View SolutionIn the system shown in figure, the block A is released from rest. Find
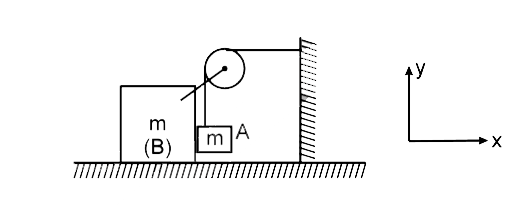
Tension in the string.View Solution